статистика::(Дискретная) функция интегральной вероятности геометрического распределения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
stats::hypergeometricCDF(N, X, n)
stats::hypergeometricCDF(N, X, n) возвращает процедуру, представляющую функцию вероятности
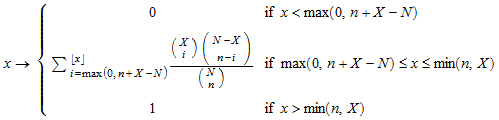
из геометрического распределения с “численностью населения” N, “численность населения успеха” X и “объем выборки” n.
Процедура f:=stats::hypergeometricCDF(N, X, n) может быть названа в форме f(x) с арифметическими выражениями x. Возвращаемое значение f(x) является или числом с плавающей запятой, точным численным значением или символьным выражением:
Если x является целым числом, рациональными или числом с плавающей точкой, в то время как N является положительным целым числом и и X и n, являются неотрицательные целые числа, то явное численное значение возвращено.
Функциональный f реагирует на свойства набора идентификаторов через assume.
Если какой-либо из параметров является символьным со свойствами можно следующим образом, то 0, 1 или символьный результат возвращен:
Если x <max (0, n + X - N), то f (x) = 0.
Если x ≥ min (n, X), то f (x) = 1.
Если X = N, то f (x) = 0 для x <n и f (x) = 1 для x ≥ n.
Если n = N, то f (x) = 0 для x <X и f (x) = 1 для x ≥ X.
Если X = N - 1, то f (x) = 0 для x <n - 1,![]() для n - 1 ≤ x <n и f (x) = 1 для x ≥ n.
для n - 1 ≤ x <n и f (x) = 1 для x ≥ n.
Если n = N - 1, то f (x) = 0 для x <X - 1,![]() для X - 1 ≤ x <X и f (x) = 1 для x ≥ X.
для X - 1 ≤ x <X и f (x) = 1 для x ≥ X.
Если X = 1, то![]() для 0 ≤ x <1 и f (x) = 1 для x ≥ 1.
для 0 ≤ x <1 и f (x) = 1 для x ≥ 1.
Если n = 1, то![]() для 0 ≤ x <1 и f (x) = 1 для x ≥ 1.
для 0 ≤ x <1 и f (x) = 1 для x ≥ 1.
Если X = 0 или n = 0, то f (x) = 1 для x ≥ 0.
Если x и все параметры, но N являются числовыми, и предположением на N является assume(N > X), то символьные значения возвращены.
f(x) отвечает на символьный звонок stats::hypergeometricCDF(N, X, n)(x) во всех других случаях.
Численные значения для N только приняты, если они - положительные целые числа.
Численные значения для X только приняты, если они - неотрицательные целые числа.
Численные значения для n только приняты, если они - неотрицательные целые числа.
Если x является числом с плавающей запятой, результатом является плавающий номер, обеспеченный N, X и n являются численными значениями. Если x является точным значением, результатом является рациональное число.
Обратите внимание на то, что для больших количеств, результаты с плавающей точкой вычисляются намного быстрее, чем точные результаты. Если приближения с плавающей точкой желаемы, передают число с плавающей запятой x stats::hypergeometricCDF.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы вычисляем функцию распределения с N = 20, X = 4 и n = 3 в различных точках:
f := stats::hypergeometricCDF(20, 4, 3): f(-1), f(0), f(1/2), f(1), f(2), f(PI), f(5)
![]()
f(-infinity), f(infinity)
![]()
f(-0.2), f(0.0), f(0.7), f(1.0), f(float(PI)), f(4.0)
![]()
delete f:
Мы используем символьные аргументы:
f := stats::hypergeometricCDF(N, X, n): f(x), f(8), f(8.0)
![]()
Когда вещественные номера присвоены N, X и n, функциональный f начинает приводить к явным результатам, если аргумент является числовым:
N := 15: X := 6: n := 5: f(0), f(1), f(2.0), f(3.5), f(4)
![]()
delete f, N, X, n:
Если один или несколько параметров являются символьными, обычно отвечают на символьный звонок. Некоторые комбинации символьных и числовых значений для N, X, n и x, однако, могут привести к символьным или числовым результатам:
f := stats::hypergeometricCDF(N, X, n): X := 1: f(-1), f(0), f(1/2), f(0.5), f(3/2), f(2.0)
![]()
X := N - 1: f(1), f(n-1), f(n)
![]()
delete X:
Если x и все параметры, но N являются числовыми, и N принят, чтобы быть больше, чем X, символьное выражение возвращено:
X := 6: assume(N > X): f := stats::hypergeometricCDF(N, X, 5): f(1), f(2), f(3)
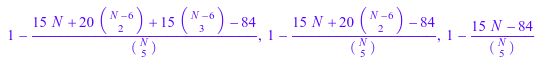
delete f, N, X:
|
“Численность населения”: арифметическое выражение, представляющее положительное целое число |
|
“Численность населения успеха”: арифметическое выражение, представляющее неотрицательное целое число |
|
“Объем выборки”: арифметическое выражение, представляющее неотрицательное целое число |