статистика::Функция квантиля распределения Пуассона
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
stats::poissonQuantile(m)
stats::poissonQuantile(m) возвращает процедуру, представляющую функцию квантиля (дискретная инверсия) кумулятивной функции распределения stats::poissonCDF(m). Для 0 ≤ x ≤ 1, k = stats::poissonQuantile(m)(x) является самым маленьким неотрицательным целочисленным удовлетворением
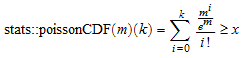 .
.
Процедура f := stats::poissonQuantile(m) может быть названа в форме f(x) с арифметическим выражением x. Возвращаемое значение вызова f(x) является или неотрицательным целым числом, infinity или символьным выражением:
Если m является неотрицательным вещественным числом и x вещественное число, удовлетворяющее 0 ≤ x <1, то f (x) возвращает неотрицательное целое число.
Если m = 0, то f (x) возвращает 0 для любого x.
Если m ≠ 0, то f (1) и f (1.0) возвращает infinity.
Во всех других случаях f(x) отвечает на символьный звонок stats::poissonQuantile(m)(x).
Численные значения для m только приняты, если они положительны.
Если аргументы с плавающей точкой передаются функции квантиля f, результат вычисляется с арифметикой с плавающей точкой. Это быстрее, чем использование точной арифметики, но результат подвергается внутренним ошибкам округления. В частности, округление может быть значительным для аргументов x близко к 1. Cf. Пример 3.
Конечные значения квантиля k = stats::poissonQuantile(m)(x) удовлетворяют
![]() .
.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Мы выполняем функцию квантиля с m = π в различных точках:
f := stats::poissonQuantile(PI): f(0), f(1/20), f(0.3), f(PI/6), f(0.7), f(1-1/10^10), f(1)
![]()
Значение f(x) удовлетворяет
![]() :
:
x := 0.98: k := f(x)
![]()
float(stats::poissonCDF(PI)(k - 1)), x, float(stats::poissonCDF(PI)(k))
![]()
delete f, x, k:
Мы используем символьные аргументы:
f := stats::poissonQuantile(m): f(x), f(9/10)
![]()
Когда m оценивает к положительному вещественному числу, функциональный f начинает производить значения квантиля:
m := 17: f(1/2), f(999/1000), f(1 - 1/10^10), f(1 - 1/10^80)
![]()
delete f, m:
Если аргументы с плавающей точкой передаются функции квантиля, результат вычисляется с арифметикой с плавающей точкой. Это быстрее, чем использование точной арифметики, но результат подвергается внутренним ошибкам округления:
f := stats::poissonQuantile(123): f(1 - 1/10^19) <> f(float(1 - 1/10^19))
![]()
delete f:
|
Среднее значение: арифметическое выражение, представляющее неотрицательное вещественное число |