Ввод::Введите представляющий усеченный Пюизе, Лорана, и расширения Ряда Тейлора
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
testtype(obj, (Puiseux | Laurent | Taylor)) testtype(obj, (Puiseux | Laurent | Taylor,x)) testtype(obj, (Puiseux | Laurent | Taylor,x = x0)) testtype(obj, (Puiseux | Laurent | Taylor,x,Undirected | Real | Right | Left)) testtype(obj, (Puiseux | Laurent | Taylor,x = x0,Undirected | Real | Right | Left))
Type::Series(Puiseux), Type::Series(Laurent) и Type::Series(Taylor) представляют усеченный ряд Пюизе, Ряд Лорана и Ряд Тейлора, соответственно.
Проверки testtype(obj, Type::Series(T)) вызова, является ли obj усеченным последовательным расширением доменного типа Series::Puiseux и математического типа T.
Вызовом, который testtype(obj, Type::Series(T, x = x0)) проверяет, кроме того, является ли серийной переменной x и точка расширения, является x0. Если x0 не использован, x0 = 0 принят.
testtype(obj, Type::Series(T, x = x0, dir)) вызова проверяет, кроме того, совместимо ли направление расширения с заданным направлением dir. Смотрите страницы справки series и Series::Puiseux для получения дополнительной информации о направлении.
Если obj имеет доменный тип Series::Puiseux, но не расширение Пюизе в математическом смысле, то testtype(obj, Type::Series(T)) возвращает FALSE. Дело обстоит так, если коэффициенты obj зависят от серийной переменной, или если флаг типа obj равняется 1. Смотрите Пример 2, и страница справки Series::Puiseux для получения дополнительной информации.
Ряд Лорана является рядом Пюизе с интегральными экспонентами. Если точка расширения конечна, то Ряд Тейлора является рядом Пюизе с неотрицательными интегральными экспонентами. Если точкой расширения является complexInfinity, то Ряд Тейлора является рядом Пюизе с неположительными интегральными экспонентами. Смотрите Пример 1 и Пример 4.
Поскольку расширение указывает infinity и -infinity, направления, Left и Right, соответственно, неявно приняты.
Определение x0 = infinity эквивалентно x0 = complexInfinity и dir = Left, и так же x0 = -infinity эквивалентен x0 = complexInfinity и dir = Right.
Смотрите пример 4.
Этот тип не представляет свойство: это не может использоваться в assume, чтобы отметить идентификатор как усеченное последовательное расширение.
Следующий вызов возвращает ряд Пюизе:
s := series(sin(sqrt(x)), x); domtype(s);
![]()
![]()
Однако s не является Ряд Лорана:
testtype(s, Type::Series(Puiseux)), testtype(s, Type::Series(Laurent)), testtype(s, Type::Series(Taylor))
![]()
Ряд Лорана, который не является Рядом Тейлора:
s := series(1/sin(x), x); domtype(s);
![]()
![]()
testtype(s, Type::Series(Puiseux)), testtype(s, Type::Series(Laurent)), testtype(s, Type::Series(Taylor))
![]()
Инверсией s является Ряд Тейлора:
1/s; testtype(1/s, Type::Series(Puiseux)), testtype(1/s, Type::Series(Laurent)), testtype(1/s, Type::Series(Taylor))
![]()
![]()
Type::Series представляет только объекты доменного типа Series::Puiseux:
s := 1 + x + 2*x^2 + O(x^3); domtype(s), testtype(s, Type::Series(Puiseux));
![]()
![]()
s := series(exp(x + 1/x), x = infinity, 3); domtype(s), testtype(s, Type::Series(Puiseux));

![]()
Для объектов доменного типа Series::Puiseux, коэффициенты которого содержат серийную переменную или чей флаг типа равняется 1, результатом является FALSE также:
s := series(psi(x), x = infinity); domtype(s), coeff(s, 0), testtype(s, Type::Series(Puiseux));
![]()
![]()
s := series(sin(sqrt(-x)), x); domtype(s), testtype(s, Type::Series(Puiseux));

![]()
Путем определения дальнейших аргументов можно проверять на серийную переменную, точку расширения и направление расширения также:
s := series(sin(sqrt(-x)), x, Left); testtype(s, Type::Series(Puiseux, y)), testtype(s, Type::Series(Puiseux, x)), testtype(s, Type::Series(Puiseux, x = 0)), testtype(s, Type::Series(Puiseux, x = 2));
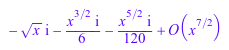
![]()
Series::Puiseux::direction(s), testtype(s, Type::Series(Puiseux, x, Undirected)), testtype(s, Type::Series(Puiseux, x, Real)), testtype(s, Type::Series(Puiseux, x, Right)), testtype(s, Type::Series(Puiseux, x, Left));
![]()
s := series(x^5/(x - 2), x = 2, 3); testtype(s, Type::Series(Laurent, x)), testtype(s, Type::Series(Laurent, x = 2)), testtype(s, Type::Series(Laurent, x = 3));
![]()
![]()
Если вы задаете направление, проверки testtype, совместимо ли это с направлением ряда:
Series::Puiseux::direction(s), testtype(s, Type::Series(Puiseux, x = 2, Undirected)), testtype(s, Type::Series(Puiseux, x = 2, Real)), testtype(s, Type::Series(Puiseux, x = 2, Right)), testtype(s, Type::Series(Puiseux, x = 2, Left));
![]()
Следующим примером является Ряд Лорана вокруг infinity, но не Ряд Тейлора:
s := series(z*exp(1/z), z = infinity); testtype(s, Type::Series(Puiseux)), testtype(s, Type::Series(Laurent)), testtype(s, Type::Series(Taylor))
![]()
![]()
Точкой расширения является infinity, или эквивалентно, complexInfinity слева:
Series::Puiseux::point(s), Series::Puiseux::direction(s); testtype(s, Type::Series(Laurent, z)), testtype(s, Type::Series(Laurent, z = 0)), testtype(s, Type::Series(Laurent, z = infinity)), testtype(s, Type::Series(Laurent, z = -infinity)), testtype(s, Type::Series(Laurent, z = complexInfinity));
![]()
![]()
testtype(s, Type::Series(Laurent, z = complexInfinity, Undirected)), testtype(s, Type::Series(Laurent, z = complexInfinity, Real)), testtype(s, Type::Series(Laurent, z = complexInfinity, Right)), testtype(s, Type::Series(Laurent, z = complexInfinity, Left));
![]()
Математически, выражение является даже неориентированным расширением вокруг complexInfinity:
s := series(z*exp(1/z), z = complexInfinity); Series::Puiseux::point(s), Series::Puiseux::direction(s);
![]()
![]()
testtype(s, Type::Series(Laurent, z)), testtype(s, Type::Series(Laurent, z = infinity)), testtype(s, Type::Series(Laurent, z = -infinity)), testtype(s, Type::Series(Laurent, z = complexInfinity));
![]()
testtype(s, Type::Series(Laurent, z = complexInfinity, Undirected)), testtype(s, Type::Series(Laurent, z = complexInfinity, Real)), testtype(s, Type::Series(Laurent, z = complexInfinity, Right)), testtype(s, Type::Series(Laurent, z = complexInfinity, Left));
![]()
|
Любой объект MuPAD® |
|
Серийная переменная: идентификатор |
|
Точка расширения: арифметическое выражение |
|
Тип ряда |
|
Направление расширения |
Смотрите testtype