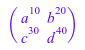Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
При выполнении основных арифметических операций на матрицах используйте типичные арифметические операторы. Например, добавьте, вычтите, умножьте и разделите следующие две матрицы при помощи стандарта +, - *, и / операторы:
A := matrix([[a, b], [c, d]]): B := matrix([[1, 2], [3, 4]]): A + B, A - B, A*B, A/B
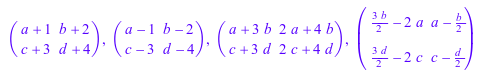
Чтобы выполнить основные операции на матрице и номере, используйте те же операторы. Когда вы умножаете матрицу на номер, MuPAD® умножает все элементы матрицы тем номером:
5*A
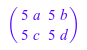
Когда вы добавляете номер в матрицу, MuPAD умножает номер на единичную матрицу, и затем добавляет результат в исходную матрицу:
A + 5
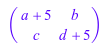
MATLAB® добавляет номер в каждый элемент матрицы. MuPAD добавляет номер только в диагональные элементы матрицы.
Можно объединить матрицы с одинаковым числом строк при помощи оператора конкатенации (.):
A.B
![]()
Помимо стандартных арифметических операций, много других функций MuPAD доступны для вычислений включающие матрицы и векторы. Чтобы проверять, принимает ли конкретная функция матрицы как параметры, смотрите раздел “Parameters” функциональной страницы справки. Следующие функции могут работать с матрицами:
Функция conjugate вычисляет сопряженный из каждого комплексного элемента матрицы:
A := matrix([[1, 2 + 3*I], [1 - I, 2*I]]): conjugate(A)
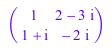
int и функции diff вычисляют производную и интеграл каждого элемента матрицы:
A := matrix(2, 2, [x, x^2, x^3, x^4]): int(A, x), diff(A, x)
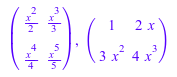
Функция expand расширяет каждый элемент матрицы:
A := matrix(2, 2, [x, (x + 1)^2, x*(x - 1), x*(x + 4)]): expand(A)
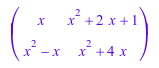
Функция map применяет заданную функцию ко всем операндам каждого элемента матрицы:
A := matrix(3, 3, [1, 2, 3], Diagonal): B := map(A, sin)
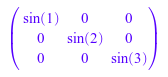
Функция float преобразовывает каждый элемент матричные или числовые подвыражения каждого элемента матрицы к числам с плавающей запятой:
float(B)

Функция evalAt (и ее ярлык |) заменяет заданным объектом другим заданным объектом, и затем оценивает каждый элемент матрицы:
A := matrix(2, 2, [x, x^2, x^3, x^4]): A|x = 2
![]()
Функция subs возвращает копию матрицы, в которой заданный объект заменяет все экземпляры другого заданного объекта. Функция не оценивает элементы матрицы после замены:
A := matrix(2, 2, [x, x^2, x^3, x^4]): subs(A, x = exp(y))
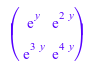
Функция has определяет, содержит ли матрица заданный объект:
A := matrix(2, 2, [x, x^2, x^3, x^4]): has(A, x^3), has(A, x^5)
![]()
Функция iszero проверяет, являются ли все элементы матрицы нулями:
A := matrix(2, 2): iszero(A)
![]()
A[1, 1] := 1: iszero(A)
![]()
Функция norm вычисляет норму бесконечности (норма суммы строки) матрицы:
A := matrix(2, 2, [a_1_1, a_1_2, a_2_1, a_2_2]): norm(A)
![]()
Функция zip(A, B, f) комбинирует матрицы A и B в матричный C так, чтобы C ij = f (A ij, B ij):
A := matrix(2, 2, [a, b, c, d]): B := matrix(2, 2, [10, 20, 30, 40]): zip(A, B, _power)