Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
Линейные преобразования являются операциями, которые матрицы выполняют на векторах. Собственным значением и собственным вектором квадратной матрицы A является, соответственно, скалярный λ и ненулевой вектор![]() , таким образом что
, таким образом что
![]() .
.
Как правило, если матрица изменяет длину вектора, но не изменяет его направление, вектор называется собственным вектором матрицы. Масштабным коэффициентом является собственное значение, сопоставленное с этим собственным вектором.
MuPAD® обеспечивает функции для вычислительных собственных значений и собственных векторов. Например, создайте следующую квадратную матрицу:
A := matrix([[1, 2, 3], [4, 5, 6], [1, 2, 3]])

Чтобы вычислить собственные значения матричного A, используйте функцию linalg::eigenvalues:
linalg::eigenvalues(A)
![]()
Функция linalg::eigenvalues возвращает набор собственных значений. Набор в MuPAD не может содержать дублирующиеся элементы. Поэтому, если матрица имеет собственные значения с кратностью, больше, чем 1, MuPAD автоматически удаляет дублирующиеся собственные значения. Если вы хотите, чтобы функция linalg::eigenvalues возвратила собственные значения наряду с их кратностью, используйте опцию Multiple. Например, нуль является двойным собственным значением матричного A:
linalg::eigenvalues(A, Multiple)
![]()
Чтобы вычислить собственные вектора матрицы, используйте функцию linalg::eigenvectors. Функция возвращает собственные вектора наряду с соответствующими собственными значениями и их кратностью:
linalg::eigenvectors(A)
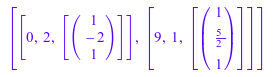
Функция linalg::eigenvalues вычисляет собственные значения матрицы путем нахождения корней характеристического полинома той матрицы. Нет никакого общего метода для решения полиномиальных уравнений порядков выше, чем 4. При попытке вычислить собственные значения большой матрицы, решатель может возвратить сложные решения или решения в форме RootOf. Кроме того, решатель может не найти решения для некоторых матриц. Например, создайте 6 ×6 матриц Паскаля:
P := linalg::pascal(6)

Для той матрицы MuPAD находит собственные значения в форме RootOf:
eigenvalues := linalg::eigenvalues(P)
![]()
Можно найти приближение с плавающей точкой результата при помощи команды float:
float(eigenvalues)
![]()
Для получения дополнительной информации о приближении собственных значений и собственных векторов численно, смотрите Числовые Собственные значения и Собственные вектора.