RootOfНабор корней полинома
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразовывают Notebook MuPAD в Live скрипты MATLAB.
RootOf(f,x) RootOf(f)
RootOf(f, x) представляет символьный набор корней полиномиального f (x) относительно неопределенного x.
RootOf служит символьным представлением нулевого набора полинома. Поскольку обычно невозможно представлять корни полинома с точки зрения радикалов, RootOf часто является единственным возможным способом представлять корни символически. RootOf в основном происходит в выводе solve или связанных функций; смотрите Пример 3.
f параметра должен быть или полиномом или арифметическим выражением, представляющим полином в x или уравнение p=q, где p и q являются арифметическими выражениями, представляющими полиномы в x. В последнем случае RootOf представляет корни p-q относительно x.
Полиномиальный f не должен быть неприводимым или даже без квадратов. Если f имеет несколько корней, RootOf представляет каждый из корней с его кратностью.
Если x не использован, то f должен быть арифметическим выражением или полиномиальным уравнением, содержащим точно одно неопределенное, и RootOf представляет корни относительно этого неопределенного.
x не должен быть идентификатором или индексированным идентификатором: это может быть любое выражение, которое не является ни рациональным, ни постоянным.
Если f содержит только один неопределенный, то можно применить float к объекту RootOf получить набор приближений с плавающей точкой для всех корней; смотрите Пример 3.
Каждый из следующих вызовов представляет корни полиномиального x 3 - x 2 относительно x, т.е. набора {0, 1}:
RootOf(x^3 - x^2, x), RootOf(x^3 = x^2, x)
![]()
RootOf(x^3 - x^2), RootOf(x^3 = x^2)
![]()
RootOf(poly(x^3 - x^2, [x]), x)
![]()
В целом, однако, RootOf только используется, когда никакое явное символьное представление корней не возможно.
Первый аргумент RootOf может содержать параметры:
RootOf(y*x^2 - x + y^2, x)
![]()
Набор корней полинома обработан как выражение. Например, это может дифференцироваться относительно свободного параметра. Результатом является набор производных корней; это выражается с точки зрения RootOf путем предоставления минимального полинома:
diff(%, y)
![]()
Для приводимых полиномов результат может быть кратным правильному минимальному полиному.
solve возвращает объекты RootOf, когда корней полинома нельзя выразить с точки зрения радикалов:
solve(x^5 + x + 7, x)
![]()
Можно применить функциональный float, чтобы получить приближения с плавающей точкой всех корней:
float(%)
![]()
Функциональный sum может вычислить суммы по всем корням данного полинома:
sum(i^2, i = RootOf(x^3 + a*x^2 + b*x + c, x))
![]()
sum(1/(z + i), i = RootOf(x^4 - y*x + 1, x))
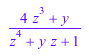
Объект RootOf представляет набор всех корней. Можно обратиться к отдельным корням через индексируемые вызовы:
RootOf(z^3 - 1, z)[i] $ i = 1..3
![]()
float(RootOf(z^3 - 1, z)[i]) $ i = 1..3
![]()
|
Полином, арифметическое выражение, представляющее полином в |
|
Неопределенное: обычно, идентификатор или индексированный идентификатор |
Символьный вызов RootOf, т.е. выражение типа "RootOf".