Документация

Используйте символьные вычисления, когда возможно

По умолчанию MuPAD выполняет вычисления в точной символьной форме. Например, стандартные математические константы имеют свои собственные символьные представительства в MuPAD. Используя эти представления, можно сохранить точное значение константы в течение вычислений. Всегда можно находить числовое приближение константы при помощи функции float:

pi := float(PI)

Избегайте ненужных преобразований в числа с плавающей запятой. Число с плавающей запятой аппроксимирует константу; это не сама константа. Используя это приближение, можно получить неправильные результаты. Например, heaviside специальная функция возвращает различные результаты для синуса π и синуса 10-разрядного приближения с плавающей точкой π:

heaviside(sin(PI)), heaviside(sin(pi))

Увеличьте точность

Риманова гипотеза утверждает, что все нетривиальные нули Дзета-функции Римана имеют ту же действительную часть. Чтобы определить местоположение возможных нулей Дзета-функции, постройте ее абсолютное значение. Следующий график показывает первые три нетривиальных корня Дзета-функции:

plot(abs(zeta(1/2 + I*y)), y = 0..30,
        AxesTitles = ["y", "|zeta|"])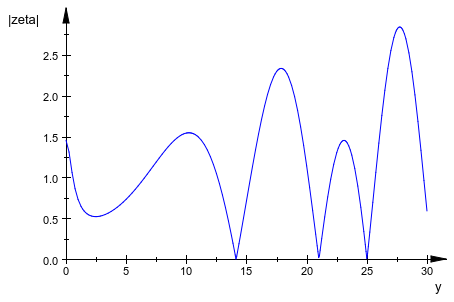

Используйте числовой решатель, чтобы аппроксимировать первые три нуля этой Дзета-функции:

numeric::solve(zeta(1/2 + I*y), y = 13..15),
numeric::solve(zeta(1/2 + I*y), y = 20..22),
numeric::solve(zeta(1/2 + I*y), y = 24..26)

Теперь, рассмотрите ту же функцию, но немного увеличьте действительную часть:. согласно Римановой гипотезе, эта функция не имеет нуля ни для какого действительного значения y. По умолчанию MuPAD использует 10 значительных десятичных цифр для вычислений, которые включают числа с плавающей запятой. Когда вы используете решатель numeric::solve с количеством по умолчанию цифр, решатель находит следующий (несуществующий) нуль Дзета-функции:

numeric::solve(zeta(1000000001/2000000000 + I*y), y = 14..15)

Увеличение чисел цифр показывает, что результат является неправильным. Дзета-функция не имеет нуля в     14 < y < 15:

DIGITS:=15:
numeric::solve(zeta(1000000001/2000000000 + I*y), y = 14..15)

delete DIGITS;

Аппроксимированные параметры и аппроксимированные результаты

Функции Бесселя с половиной целочисленных индексов возвращают точные символьные выражения. Аппроксимируя эти выражения числами с плавающей запятой, можно получить очень нестабильные результаты. Например, точное символьное выражение для следующей Функции Бесселя:

B := besselJ(53/2, PI)

Используйте команду float, чтобы аппроксимировать это выражение численно:

float(B)

Теперь, вызовите Функцию Бесселя с параметром с плавающей точкой. Значительная разница в этих двух приближениях указывает, что один или оба результата являются неправильными:

besselJ(53/2, float(PI))

Увеличьте числовую рабочую точность, чтобы получить более точные приближения:

DIGITS:= 45: float(B); besselJ(53/2, float(PI))

delete DIGITS;

Теперь вы видите, что использование параметра с плавающей точкой, чтобы вычислить Функцию Бесселя приводит к правильному результату (в рабочей точности). Приближение точного символьного выражения, для которого Функция Бесселя возвращает неправильный результат из-за числовой нестабильности.

Постройте специальные функции

Графический вывод функции может помочь вам распознать неправильные приближения с плавающей точкой. Например, числовое приближение следующей Функции Бесселя возвращается:

B := besselJ(53/2, PI):
float(B)

Постройте функцию для значений x вокруг 53/2. График функций показывает, что приближение с плавающей точкой является неправильным:

plot(besselJ(x, PI), x = 26..27)

Иногда, чтобы видеть, что приближение с плавающей точкой является неправильным, необходимо масштабировать конкретные части графика функций. Например, числовой решатель находит неожиданный нуль Дзета-функции:

numeric::solve(zeta(1000000001/2000000000 + I*y), y = 14..15)

Чтобы заняться расследованиями, имеет ли Дзета-функция на самом деле нуль в той точке или появляется ли результат из-за ошибки округления, постройте абсолютное значение Дзета-функции.

plot(abs(zeta(1000000001/2000000000 + I*y)), y = 0..30,
                          AxesTitles = ["y", "|zeta|"])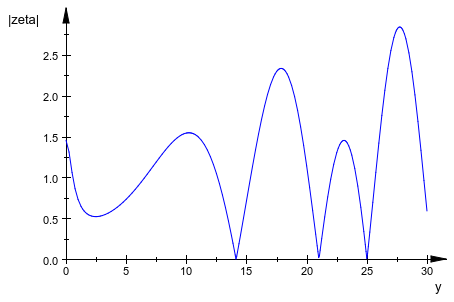

Чтобы видеть больше деталей графика функций около возможного нуля, масштабируйте график. Чтобы видеть, что числовой результат является неправильным, увеличьте ту часть графика функций вне числовой рабочей точности, и затем переоцените график. Когда вы масштабируете и переоцениваете, MuPAD повторно вычисляет часть графика функций с увеличенной числовой точностью.

Чтобы получить точные результаты после изменения масштаба графика, используйте кнопку Recalculate. После изменения масштаба и переоценки графика, вы видите, что функция не имеет нуля в том интервале.