Документация

Установите постоянные предположения

Постоянные предположения работают лучше всего на математические свойства, которые сохраняются в течение ваших вычислений. Предположим, вы хотите вычислить время, в течение которого свободно падающий объект исключает из высоты h. Кинематическим уравнением для движения свободного падения является h = g t2, где g является ускорением свободного падения. Используя это уравнение, вычислите время, в течение которого объект падает от определенной высоты. Без предположений вы получаете полное решение для всех возможных значений параметров включая комплексные числа:

t = solve(h = g*t^2/2, t)

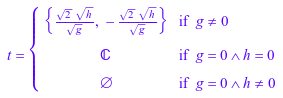
Если вы не рассматриваете особый случай, где никакие гравитационные силы не существуют, можно безопасно принять, что гравитационное ускорение положительно. Это предположение удаляет специальные случаи невесомости из решения:

assume(g > 0);
t = solve(h = g*t^2/2, t)

Переменная h в уравнении представляет высоту, от которой падает объект. Если вы не полагаете, что кто-то первоначально выдает объект вверх и что объект отражается от земли, высота, h всегда положителен. Поэтому можно принять, что и гравитационное ускорение g и высота h положительны:

assume(g > 0 and h > 0);
t = solve(h = g*t^2/2, t)

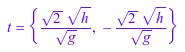
Предположение, что время отбрасывания является положительным значением, вы получаете ожидаемый результат. Когда вы устанавливаете предположения на переменных, решатель сравнивает полученные решения с заданными предположениями. Эта дополнительная задача может замедлить решатель:

assume(g > 0 and h > 0 and t > 0);
t := solve(h = g*t^2/2, t)

Решатель возвращает решения как набор, даже если набор содержит только один элемент. Чтобы получить доступ к элементам набора решения, используйте квадратные скобки или команду op:

time = t[1]

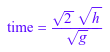
Очистите переменную t для дальнейших вычислений:

delete t

Если вы устанавливаете несколько предположений для того же объекта, каждое новое предположение перезаписывает предыдущий:

assume(h in R_);
assume(h <> 0);
is(h in R_), is(h <> 0)

Если вы хотите сохранить предыдущее предположение при добавлении нового смотрите Добавляющие Предположения.

Команда assume не может решить предположения в форме уравнений и не присваивает значения переменным:

assume(g + 5 = 14.8 and 2*t = 14);
h = g*t^2/2

Когда вы устанавливаете предположение в форме неравенства, обе стороны неравенства должны представлять действительные значения. Неравенства с комплексными числами недопустимы, потому что поле комплексных чисел не является упорядоченным полем. Например, при попытке использовать следующее предположение, MuPAD^® возвращает ошибку:

assume(t > 2*I)

Error: Inconsistent assumptions. [property::_assume]

Можно использовать комплексные числа в предположении, записанном в форме уравнения:

assume(t = 2*PI*I)

Добавьте постоянные предположения

Когда вы устанавливаете предположение на объекте, MuPAD заменяет предыдущие предположения на том объекте с новым предположением:

assume(x in Z_);
assume(x in R_);
is(x in Z_), is(x in R_)

Чтобы добавить новое предположение, не удаляя предыдущие предположения, используйте команду assumeAlso:

assume(x in Z_);
assumeAlso(x in R_);
is(x in Z_), is(x in R_)

Кроме того, можно установить несколько предположений в одном вызове функции при помощи логических операторов. Например, установите два предположения на x:

assume(x in Z_ and x in R_);
is(x in Z_), is(x in R_)

При добавлении предположений всегда проверяйте, что новое предположение не противоречит существующему предположению. MuPAD не гарантирует, что обнаружил конфликтные предположения. Например, примите, что y является одновременно ненулевым, действительным и мнимое значение. Type::Imaginary относится ко всем комплексным числам, лежащим на мнимой оси. Когда вы устанавливаете эти предположения, MuPAD не выдает предупреждения и не делает ошибки:

assume(y <> 0);
assumeAlso(y in R_);
assumeAlso(y, Type::Imaginary)

Чтобы проверять, сохраняется ли предположение все еще, используйте команду is. Например, MuPAD пропускает предположение, что переменная y представляет мнимые числа, потому что это предположение конфликтует с комбинацией предыдущих двух предположений:

is(y <> 0), is(y in R_), is(y, Type::Imaginary)

Если вы устанавливаете конфликтные предположения, порядок, в котором вы устанавливаете их, не всегда определяет, какое предположение MuPAD принимает:

assume(y <> 0);
assumeAlso(y, Type::Imaginary);
assumeAlso(y in Z_);
is(y <> 0), is(y, Type::Imaginary), is(y in Z_)

Очистите постоянные предположения

Постоянные предположения содержат для всех дальнейших вычислений. Перед использованием параметра в других вычислениях проверяйте, какие свойства MuPAD принимает, чтобы быть допустимым для этого параметра. Команда property::showprops возвращает все предположения, заданные для параметра:

assume(g in R_);
assume(h in Z_);
assume(t > 0);
property::showprops(g),
property::showprops(h),
property::showprops(t)

Команда unassume очищает конкретный объект от всех предположений:

unassume(g);
unassume(h);
unassume(t);
property::showprops(g),
property::showprops(h),
property::showprops(t)

Чтобы удалить значение параметра и очистить весь набор предположений для этого параметра, используйте команду delete:

delete g, h, t

Например, присвойте значение переменной h и примите что h > 0:

h := g*t^2/2:
assume(g > 0 and h > 0);
property::showprops(h); h

Команда unassume очищает предположение, но не удаляет значение переменной:

unassume(h > 0);
property::showprops(h); h

Команда delete очищает предположение и значение:

delete h;
property::showprops(h); h