Поскольку CWT является избыточным преобразованием, и коэффициенты CWT зависят от вейвлета, это может быть сложно, чтобы интерпретировать результаты.
Чтобы помочь вам в интерпретации коэффициентов CWT, лучше запускаться с простого сигнала анализировать и вейвлет анализа с простой структурой.
Функцией сигнала, что вейвлеты очень хороши в обнаружении, является разрыв или особенность. Резкие переходы в сигналах приводят к коэффициентам вейвлета с большими абсолютными значениями.
Поскольку сигнал создает переключенный импульс. Импульс происходит в точке 500.
x = zeros(1000,1); x(500) = 1;
Для вейвлета выберите вейвлет Хаара.
[~,psi,xval] = wavefun('haar',10);
plot(xval,psi); axis([0 1 -1.5 1.5]);
title('Haar Wavelet');
Вычислить CWT с помощью вейвлета Хаара в шкалах 1 - 128, введите:
CWTcoeffs = cwt(x,1:128,'haar');
CWTcoeffs 128 1000 матрица. Каждая строка матрицы содержит коэффициенты CWT для одной шкалы. Существует 128 строк, потому что входом SCALES к cwt является 1:128. Размерность столбца матрицы совпадает с длиной входного сигнала.
Вспомните, что CWT 1D сигнал является функцией параметров положения и шкалы. Чтобы произвести график коэффициентов CWT, постройте положение вдоль x - оси, шкалы вдоль y - ось, и закодировать значение или размер коэффициентов CWT как цвет в каждой точке в x-y или плоскость масштаба времени.
Можно произвести этот график с помощью cwt с дополнительным входным параметром 'plot'.
cwt(x,1:128,'haar','plot'); colormap jet; colorbar;
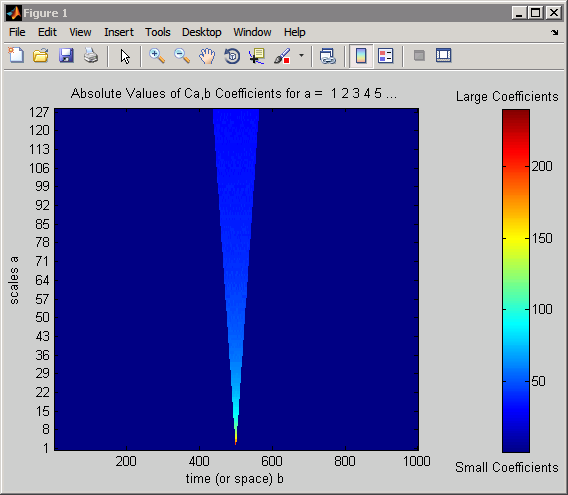
Предыдущая фигура была изменена с текстовыми метками, чтобы явным образом показать, какие цвета указывают на большие и маленькие коэффициенты CWT.
Можно также построить размер коэффициентов CWT в 3D с
cwt(x,1:64,'haar','3Dplot'); colormap jet;
Исследуя CWT переключенного импульсного сигнала, вы видите, что набор больших коэффициентов CWT сконцентрирован в узкой области в плоскости масштаба времени в мелких масштабах, сосредоточенных вокруг точки 500. Когда шкала увеличивается, набор больших коэффициентов CWT становится более широким, но остается в центре вокруг точки 500. Если вы прослеживаете границу этой области, она напоминает следующую фигуру.
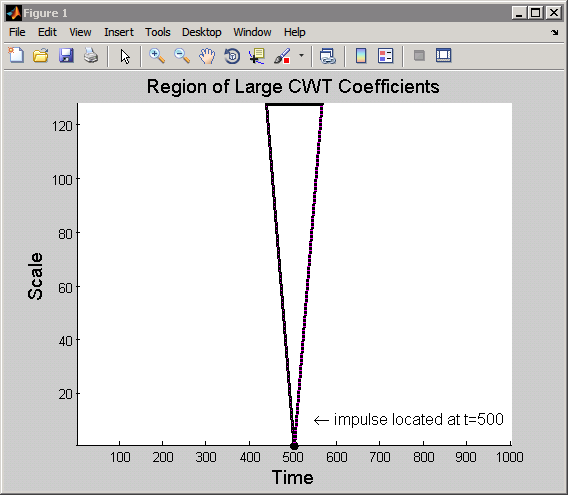
Эта область упоминается как конус влияния точки t =500 для вейвлета Хаара. Для данной точки конус влияния показывает вам, какие коэффициенты CWT затронуты значением сигналов в той точке.
Чтобы понять конус влияния, примите, что вам поддержали вейвлет на [-C, C]. Сдвиг вейвлета b и масштабирование a приводят к вейвлету, поддержанному на [-Ca+b, Ca+b]. Для простого случая переключенного импульса, , коэффициенты CWT являются только ненулевыми в интервале вокруг τ, равного поддержке вейвлета в каждой шкале. Вы видите это путем рассмотрения формального выражения CWT переключенного импульса.
Для импульса коэффициенты CWT равны спрягаемому, инвертированному временем, и масштабируемому вейвлету как функция параметра сдвига, b. Вы видите это путем графического вывода коэффициентов CWT для выбора немного шкал.
subplot(311)
plot(CWTcoeffs(10,:)); title('Scale 10');
subplot(312)
plot(CWTcoeffs(50,:)); title('Scale 50');
subplot(313)
plot(CWTcoeffs(90,:)); title('Scale 90');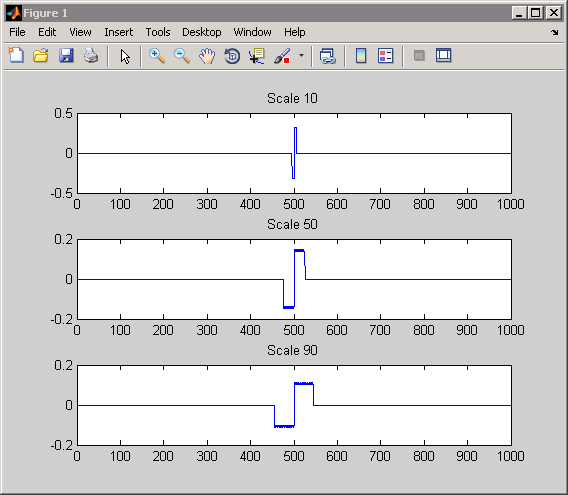
Конус влияния зависит от вейвлета. Можно найти и построить конус влияния за определенный вейвлет с conofinf.
Следующий пример показывает суперпозицию двух переключенных импульсов, . В этом случае используйте экстремальный вейвлет фазы Добечиса с четырьмя исчезающими моментами, db4. Следующие данные показывают конус влияния за точки 300 и 500 с помощью вейвлета db4.
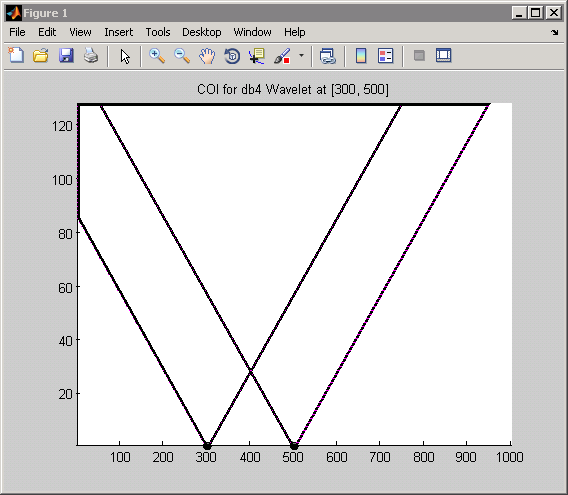
Посмотрите на точку 400 для шкалы 20. В той шкале вы видите, что никакой конус влияния не перекрывает точку 400. Поэтому можно ожидать, что коэффициент CWT будет нулем в той точке и шкале. Сигнал является только ненулевым в двух значениях, 300 и 500, и никакой конус влияния за те значения не включает точку 400 в шкалу 20. Можно подтвердить это путем ввода:
x = zeros(1000,1); x([300 500]) = 1; CWTcoeffs = cwt(x,1:128,'db4'); plot(CWTcoeffs(20,:)); grid on;
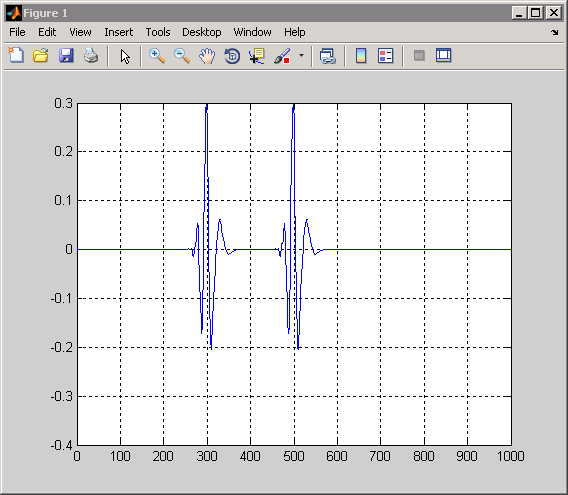
Затем, посмотрите на точку 400 в шкале 80. В шкале 80, конусы влияния за обе точки 300 и 500 включают точку 400. Даже при том, что сигнал является нулем в точке 400, вы получаете ненулевой коэффициент CWT в той шкале. Коэффициент CWT является ненулевым, потому что поддержка вейвлета стала достаточно большой в той шкале, чтобы позволить значениям сигналов 100 точек выше и ниже влиять на коэффициент CWT. Можно подтвердить это путем ввода:
plot(CWTcoeffs(80,:)); grid on;
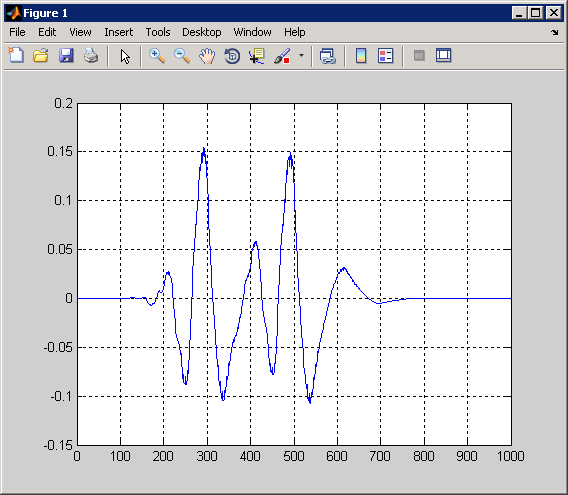
В предыдущем примере коэффициенты CWT стали большими около резкого изменения в сигнале. Эта способность обнаружить разрывы является силой вейвлета, преобразовывают. Предыдущий пример также продемонстрировал, что коэффициенты CWT локализуют разрыв лучше всего в мелких масштабах. В мелких масштабах маленькая поддержка вейвлета гарантирует, что особенность только влияет на маленький набор коэффициентов вейвлета.
Продемонстрировать, почему вейвлет преобразовывает, так владеет мастерством обнаружения резких изменений в сигнале, рассмотрите переключенный Heaviside или модульный сигнал шага.
x = [zeros(500,1); ones(500,1)]; CWTcoeffs = cwt(x,1:64,'haar','plot'); colormap jet;
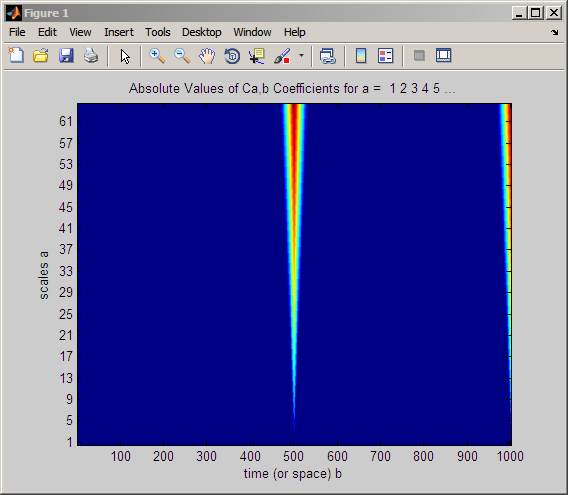
Подобно переключенному импульсному примеру резкий переход в переключенной ступенчатой функции приводит к большим коэффициентам CWT в разрыве. Следующая фигура иллюстрирует, почему это происходит.
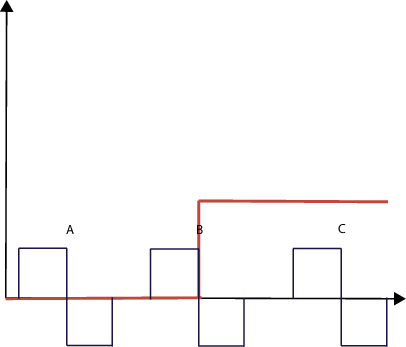
В предыдущей фигуре красная функция является переключенной модульной ступенчатой функцией. Черные функции маркировали A, B, и C изображает вейвлеты Хаара в той же шкале, но различных положениях. Вы видите, что коэффициенты CWT вокруг положения A являются нулем. Сигнал является нулем в том окружении, и поэтому вейвлет преобразовывает, также нуль, потому что любой вейвлет объединяется, чтобы обнулить.
Отметьте вейвлет Хаара, сосредоточенный вокруг положения B. Отрицательная часть вейвлета Хаара накладывается с областью ступенчатой функции, которая равна 1. Коэффициенты CWT отрицательны, потому что продуктом вейвлета Хаара и модульного шага является отрицательная константа. Интеграция по той области приводит к отрицательному числу.
Отметьте вейвлет Хаара, сосредоточенный вокруг положения C. Здесь коэффициенты CWT являются нулем. Ступенчатая функция равна одной. Продукт вейвлета со ступенчатой функцией равен вейвлету. Интеграция любого вейвлета по его поддержке является нулем. Это - нулевое свойство момента вейвлетов.
В положении B вейвлет Хаара уже переключил в ненулевой фрагмент ступенчатой функции 1/2 ее поддержки. Как только поддержка вейвлета пересекается с фрагментом единицы ступенчатой функции, коэффициенты CWT являются ненулевыми. На самом деле ситуация, проиллюстрированная в предыдущей фигуре, совпадает с коэффициентами CWT, достигающими их самого большого абсолютного значения. Это вызвано тем, что целое отрицательное отклонение колебания вейвлета накладывается с фрагментом единицы модульного шага, в то время как ни одно из положительного отклонения вейвлета не делает. Если вейвлет переключает до такой степени, что положительные перекрытия отклонения с модульным шагом, будет некоторый позитивный вклад к интегралу. Коэффициенты вейвлета все еще отрицательны (отрицательный фрагмент интеграла больше в области), но они меньше в абсолютном значении, чем полученные в положении B.
Следующая фигура иллюстрирует два других положения, где вейвлет пересекает фрагмент единицы модульного шага.
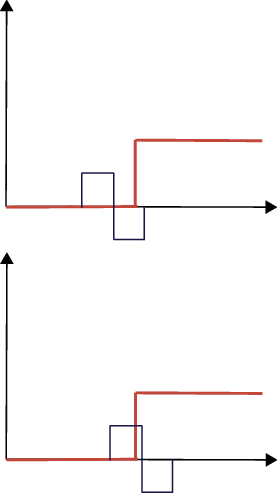
В главной фигуре вейвлет только что начал накладываться с фрагментом единицы модульного шага. В этом случае коэффициенты CWT являются отрицательными, но не столь большими в абсолютном значении как полученные в положении B. В нижней фигуре вейвлет переключил прошлое положение B, и положительное отклонение вейвлета начинает способствовать интегралу. Коэффициенты CWT являются все еще отрицательными, но не столь большими в абсолютном значении как полученные в положении B.
Можно теперь визуализировать, как вейвлет преобразовывает, может обнаружить разрывы. Можно также визуализировать в этом простом примере точно, почему коэффициенты CWT отрицательны в CWT переключенного модульного шага с помощью вейвлета Хаара. Обратите внимание на то, что это поведение отличается для других вейвлетов.
x = [zeros(500,1); ones(500,1)];
CWTcoeffs = cwt(x,1:64,'haar','plot'); colormap jet;
% plot a few scales for visualization
subplot(311);
plot(CWTcoeffs(5,:)); title('Scale 5');
subplot(312);
plot(CWTcoeffs(10,:)); title('Scale 10');
subplot(313);
plot(CWTcoeffs(50,:)); title('Scale 50');Затем рассмотрите, как CWT представляет сглаженные сигналы. Поскольку синусоидальные колебания являются общим явлением, этот раздел исследует как синусоидальные колебания во влиянии сигнала коэффициенты CWT. Чтобы начаться, считайте вейвлет sym4 в определенной шкале наложенным на синусоиду.
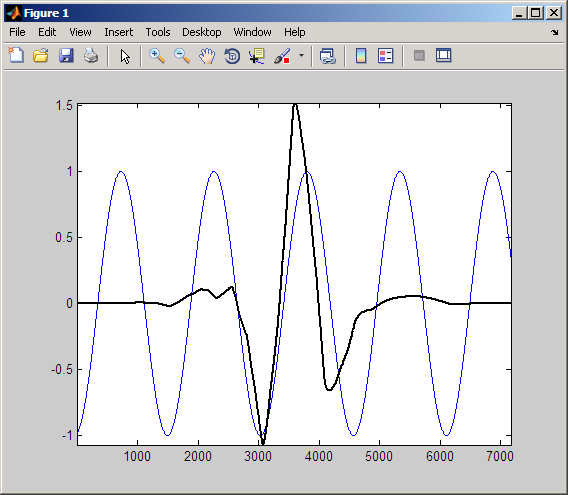
Вспомните, что коэффициенты CWT получены путем вычисления продукта сигнала с переключенным и масштабировали вейвлет анализа и интеграцию результата. Следующие данные показывают продукт вейвлета и синусоиды от предыдущей фигуры.
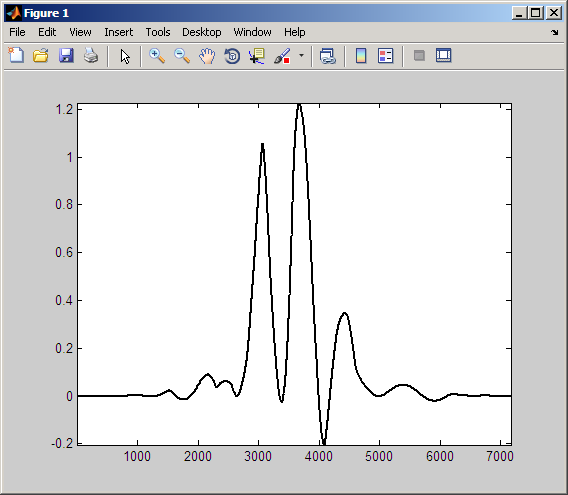
Вы видите, что интеграция по этому продукту производит положительный коэффициент CWT. Это заканчивается, потому что колебание в вейвлете приблизительно совпадает с периодом синусоиды. Вейвлет совпадает с синусоидой. Отрицательные отклонения вейвлета приблизительно совпадают с отрицательными отклонениями синусоиды. То же самое верно для положительных отклонений и вейвлета и синусоиды.
Следующие переводы на цифровой регистр вейвлет 1/2 периода синусоиды.
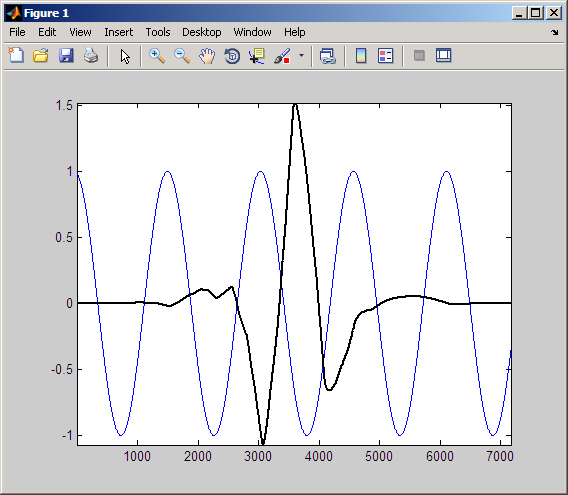
Исследуйте продукт переключенного вейвлета и синусоиды.
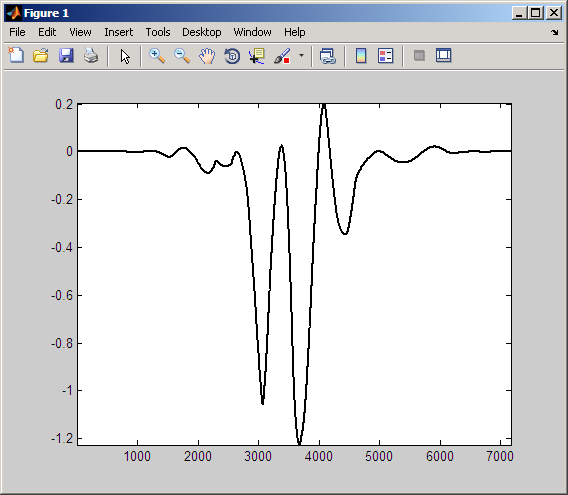
Вы видите, что интеграция по этому продукту производит отрицательный коэффициент CWT. Это заканчивается, потому что вейвлет является 1/2 циклом, несовпадающим по фазе с синусоидой. Отрицательные отклонения вейвлета приблизительно совпадают с положительными отклонениями синусоиды. Положительные отклонения вейвлета приблизительно совпадают с отрицательными отклонениями синусоиды.
Наконец, переключите вейвлет приблизительно один цикл четверти синусоиды.
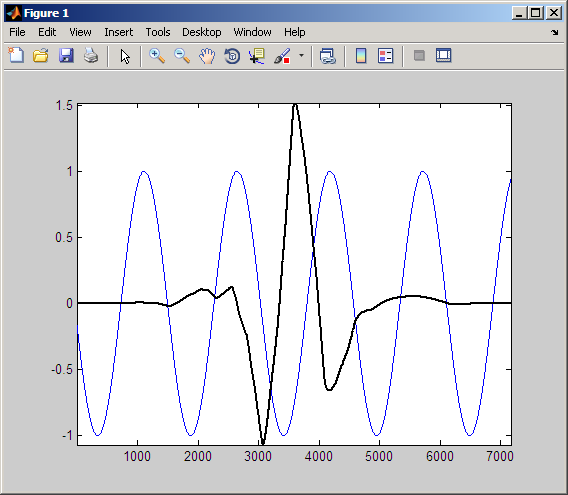
Следующие данные показывают продукт переключенного вейвлета и синусоиды.
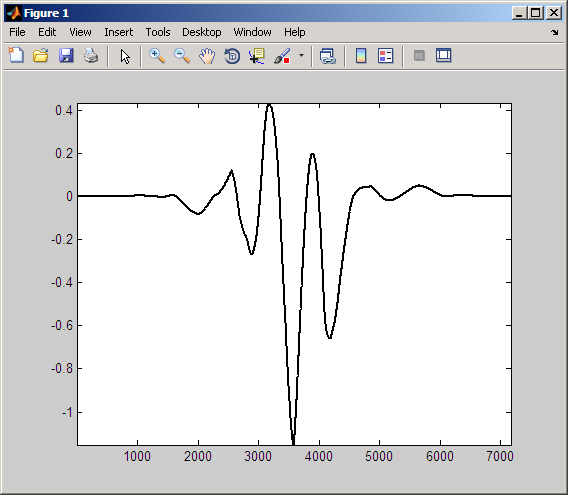
Интеграция по этому продукту производит коэффициент CWT, намного меньший в абсолютном значении, чем любой из этих двух предыдущих примеров. Это заканчивается, потому что отрицательное отклонение вейвлета приблизительно выравнивается с положительным отклонением синусоиды. Кроме того, основное положительное отклонение вейвлета приблизительно выравнивается с положительным отклонением синусоиды. Получившийся продукт намного больше походит на вейвлет, чем другие два продукта. Если бы это походило точно на вейвлет, интеграл был бы нулем.
В шкалах, где колебание в вейвлете происходит или в большом количестве более широкого или в меньшего масштаба, чем период синусоиды, вы получаете коэффициенты CWT около нуля. Следующая фигура иллюстрирует случай, где вейвлет колеблется в намного меньшей шкале, чем синусоида.
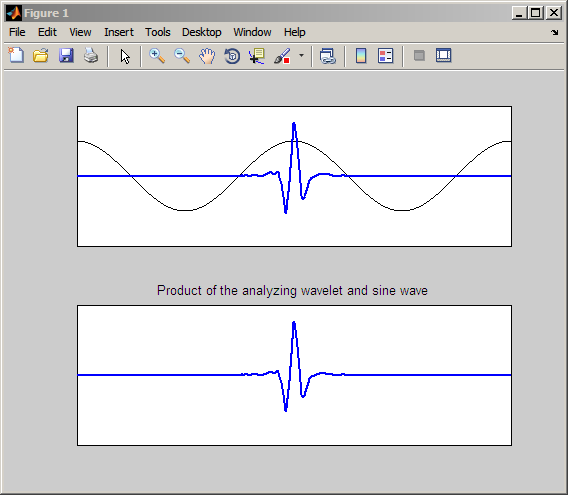
Продукт, показанный в нижней области тесно, напоминает вейвлет анализа. Интеграция этого продукта приводит к коэффициенту CWT около нуля.
Следующий пример создает синусоиду на 60 Гц и получает CWT с помощью вейвлета sym8.
t = linspace(0,1,1000); x = cos(2*pi*60*t); CWTcoeffs = cwt(x,1:64,'sym8','plot'); colormap jet;
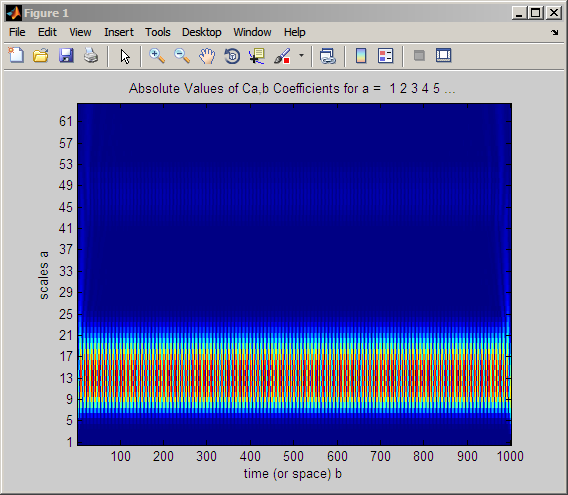
Обратите внимание на то, что коэффициенты CWT являются большими в абсолютном значении вокруг шкал 9 - 21. Можно найти псевдочастоты, соответствующие этим шкалам с помощью команды:
freq = scal2frq(9:21,'sym8',1/1000);
Обратите внимание на то, что коэффициенты CWT являются большими в шкалах около частоты синусоиды. Можно ясно видеть синусоидальный шаблон в коэффициентах CWT в этих шкалах со следующим кодом.
surf(CWTcoeffs); colormap jet;
shading('interp'); view(-60,12);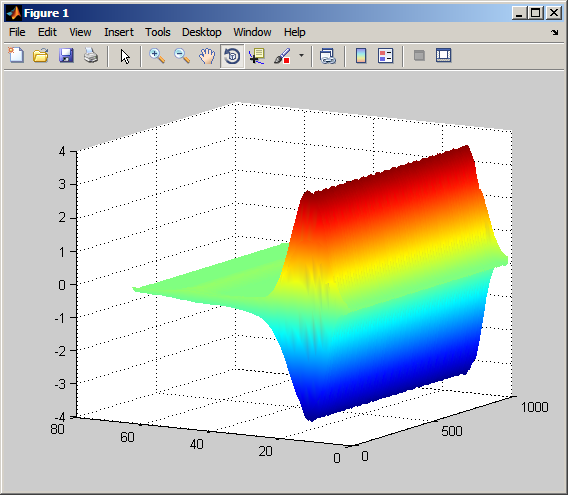
Итоговый пример создает сигнал, состоящий из обоих резких переходов и сглаженных колебаний. Сигнал является синусоидой на 2 Гц с двумя введенными разрывами.
N = 1024;
t = linspace(0,1,1024);
x = 4*sin(4*pi*t);
x = x - sign(t - .3) - sign(.72 - t);
plot(t,x); xlabel('t'); ylabel('x');
grid on;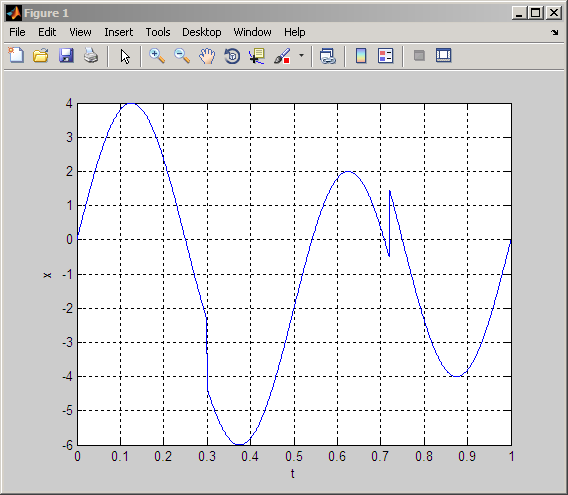
Отметьте разрывы рядом t=0.3 и t=0.7.
Получите и постройте CWT с помощью вейвлета sym4.
CWTcoeffs = cwt(x,1:180,'sym4');
imagesc(t,1:180,abs(CWTcoeffs));
colormap jet; axis xy;
xlabel('t'); ylabel('Scales');
Обратите внимание на то, что CWT обнаруживает и резкие переходы и колебания в сигнале. Резкие переходы влияют на коэффициенты CWT во всех шкалах и ясно разделяют себя от более сглаженных функций сигнала в мелких масштабах. С другой стороны, максимумы и минимумы синусоиды на 2 Гц очевидны в коэффициентах CWT в крупных масштабах и не очевидны в мелких масштабах.
Следующие общие принципы важны, чтобы иметь в виду при интерпретации коэффициентов CWT.
Конус влияния — В зависимости от шкалы, коэффициент CWT в точке может быть затронут значениями сигналов в точках, далеко удаленных. Необходимо учесть поддержку вейвлета в определенных шкалах. Используйте conofinf, чтобы определить конус влияния. Не все вейвлеты равны в своей поддержке. Например, вейвлет Хаара имеет меньшую поддержку во всех шкалах, чем вейвлет sym4.
При обнаружении резких переходов — Вейвлеты очень полезны для обнаружения резких изменений в сигнале. Резкие изменения в продукте сигнала относительно большие коэффициенты вейвлета (в абсолютном значении) сосредоточенный вокруг разрыва во всех шкалах. Из-за поддержки вейвлета набор коэффициентов CWT, затронутых особенностью, увеличивается с увеличивающейся шкалой. Вспомните, что это - определение конуса влияния. Самая точная локализация разрыва на основе коэффициентов CWT получена в самых маленьких шкалах.
Обнаружение сглаженных функций сигнала — Сглаженные функции сигнала производят относительно большие коэффициенты вейвлета в шкалах, где колебание в вейвлете коррелирует лучше всего с функцией сигнала. Для синусоидальных колебаний коэффициенты CWT отображают колебательный шаблон в шкалах, где колебание в вейвлете аппроксимирует период синусоиды.
Основной алгоритм для непрерывного вейвлета преобразовывает (CWT):
Возьмите вейвлет и сравните его с разделом в начале исходного сигнала.
Вычислите номер, C, который представляет, как тесно коррелированый вейвлет с этим разделом сигнала. Чем больше номер C находится в абсолютном значении, тем больше подобие. Это следует из факта, коэффициенты CWT вычисляются со скалярным произведением. Смотрите Скалярные произведения для получения дополнительной информации о том, как скалярные произведения измеряют подобие. Если энергия сигнала и энергия вейвлета равны одной, C может быть интерпретирован как коэффициент корреляции. Обратите внимание на то, что, в целом, энергия сигнала не равняется один, и коэффициенты CWT не являются непосредственно поддающимися толкованию как коэффициенты корреляции.
Как описано в Непрерывных и Дискретных Преобразованиях Вейвлета, коэффициенты CWT явным образом зависят от вейвлета анализа. Поэтому коэффициенты CWT отличаются, когда вы вычисляете CWT для того же сигнала с помощью различных вейвлетов.
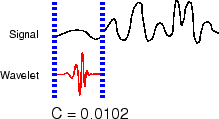
Переключите вейвлет к правильным и повторным шагам 1 и 2, пока вы не покрыли целый сигнал.
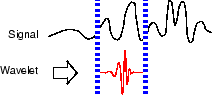
Шкала (фрагмент) вейвлет и повторные шаги 1 - 3.
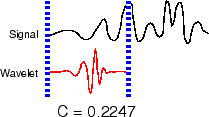
Повторите шаги 1 - 4 для всех шкал.