Непрерывный 1D вейвлет преобразовывает
Смотрите cwt для получения информации о более старой версии cwt. Более старая версия больше не рекомендуется.
wt = cwt(x)wt = cwt(x,wname)[wt,f] =
cwt(___,fs)[wt,period]
= cwt(___,ts)[wt,f,coi]
= cwt(___,fs)[wt,period,coi]
= cwt(___,ts)[___] = cwt(___,Name,Value)[___,coi,fb] = cwt(___)[___,fb,scalingcfs] = cwt(___)cwt(___)wt = cwt(x)x. Вход, x, является действительной двойной точностью - или комплексный вектор, или одно-переменный регулярно выбирал расписание и должен иметь по крайней мере четыре выборки. CWT получен с помощью аналитического вейвлета Морзе с параметром симметрии (гамма), равная 3 и продукт пропускной способности времени, равный 60. cwt использует 10 речи на октаву. Минимальные и максимальные шкалы определяются автоматически на основе энергетического распространения вейвлета в частоте и время. Если x с действительным знаком, wt является 2D матрицей, где каждая строка соответствует одной шкале. Размер столбца wt равен длине x. Если x с комплексным знаком, wt является 3-D матрицей, где первой страницей является CWT для положительных шкал (аналитическая часть или против часовой стрелки компонент), и второй страницей является CWT для отрицательных шкал (антианалитическая часть или по часовой стрелке компонент).
Функция cwt использует нормализацию L1. С нормализацией L1, если у вас есть равные амплитудные колебательные компоненты в ваших данных в различных шкалах, у них будет равное значение в CWT. Используя нормализацию L1 показывает более точное представление сигнала. См. Норму L1 для CWT и Содействующих Амплитуд Синусоиды и Вейвлета.
Функция cwt поддерживает генерацию кода графического процессора. Смотрите Генерацию кода графического процессора для получения дополнительной информации.
[ задает частоту дискретизации, wt,f] =
cwt(___,fs)fs, в Гц как положительная скалярная величина. cwt использует fs, чтобы определить преобразования шкалы к частоте и возвращает частоты f в Гц. Если вы не задаете частоту дискретизации, cwt возвращает f в циклах на выборку. Если вход x является комплексным, преобразования шкалы к частоте применяются к обеим страницам wt. Если x является расписанием, вы не можете задать fs. fs определяется от RowTimes расписания.
[ задает период выборки, wt,period]
= cwt(___,ts)ts, как положительный скаляр duration. duration может быть в годах, днях, часах, минутах или секундах. cwt использует ts, чтобы вычислить преобразование шкалы к периоду и возвращает периоды времени в period. Массив длительности в period имеет то же свойство формата как ts. Если вход x является комплексным, преобразования шкалы к периоду применяются к обеим страницам wt. Если x является расписанием, вы не можете задать ts. ts определяется от RowTimes расписания, когда вы устанавливаете пару "имя-значение" 'PeriodLimits'.
[___] = cwt(___, возвращает CWT с дополнительными опциями, заданными одним или несколькими аргументами пары Name,Value)Name,Value.
[___, возвращает набор фильтров, используемый в CWT. Смотрите coi,fb] = cwt(___)cwtfilterbank.
[___, возвращает масштабные коэффициенты, если вейвлетом анализа является fb,scalingcfs] = cwt(___)'morse' или 'amor'. Масштабные коэффициенты не поддержаны для вейвлета удара.
cwt(___) без выходных аргументов строит CWT scalogram. scalogram является абсолютным значением CWT как функция времени и частоты. Частота построена на логарифмическом масштабе. Конус влияния, показывающего, где краевые эффекты становятся значительными, также построен. Серые области вне пунктирной белой строки формируют рисунок областей, где краевые эффекты являются значительными. Если входной сигнал с комплексным знаком, положительное (против часовой стрелки) и отрицательный (по часовой стрелке), компоненты построены в отдельном scalograms.
Если вы не задаете частоту дискретизации или период выборки, частоты построены в циклах на выборку. Если вы задаете частоту дискретизации, частоты находятся в Гц. Если вы задаете период выборки, scalogram построен как функция времени и периодов. Если входной сигнал является расписанием, scalogram построен как функция времени и частоты в герц и использует RowTimes в качестве основания для оси времени.
Чтобы видеть время, частота и значение точки scalogram, включают всплывающие подсказки на панели инструментов осей вращения и кликают по желаемой точке в scalogram.
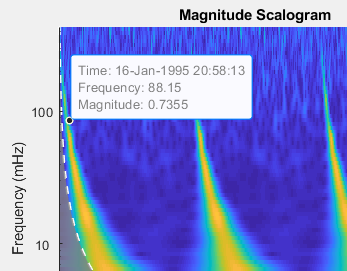
Перед графическим выводом cwt очищает (clf) текущую фигуру. Чтобы построить scalogram в подграфике, используйте функцию построения графика.
Если вы берете CWT нескольких временных рядов, более эффективно предварительно вычислить и использовать набор фильтров CWT, чем, неоднократно применяют функцию cwt. Смотрите Используя Набор фильтров CWT на Нескольких Временных рядах.
[1] Лилли, J. M. и С. К. Олхед. “Обобщенные Вейвлеты Азбуки Морзе как Суперсемейство Аналитических Вейвлетов”. Транзакции IEEE на Обработке сигналов. Издание 60, № 11, 2012, стр 6036–6041.
[2] Лилли, J. M. и С. К. Олхед. “Свойства высшего порядка Аналитических Вейвлетов”. Транзакции IEEE на Обработке сигналов. Издание 57, № 1, 2009, стр 146–160.
[3] Лилли, J. M. jLab: пакет анализа данных для MATLAB, версии 1.6.2. 2016. http://www.jmlilly.net/jmlsoft.html.
[4] Лилли, J. M. “Элементный анализ: основанный на вейвлете метод для анализа локализованных временем событий в шумных временных рядах”. Продолжения Королевского общества A. Объем 473: 20160776, 2017, стр 1–28. dx.doi.org/10.1098/rspa.2016.0776.