Вейвлет и масштабирующиеся 2D функции
[PHI,PSI,XVAL] = wavefun('wname',ITER)
[S,W1,W2,W3,XYVAL] = wavefun2('wname',ITER,'plot')
[S,W1,W2,W3,XYVAL] = wavefun2(wname,A,B)
[S,W1,W2,W3,XYVAL] = wavefun2('wname',max(A,B))
[S,W1,W2,W3,XYVAL] = wavefun2('wname',0)
[S,W1,W2,W3,XYVAL] = wavefun2('wname',4,0)
[S,W1,W2,W3,XYVAL] = wavefun2('wname')
[S,W1,W2,W3,XYVAL] = wavefun2('wname',4)
Для ортогонального вейвлета 'wname' wavefun2 возвращает масштабирующуюся функцию и три функции вейвлета, следующие из продуктов тензора одномерного масштабирования и функций вейвлета.
Если [PHI,PSI,XVAL] = wavefun(, масштабирующийся функциональный 'wname',ITER)S является продуктом тензора PHI и PSI.
Функции вейвлета W1, W2 и W3 являются продуктами тензора (PHI, PSI), (PSI, PHI), и (PSI, PSI), соответственно.
Двумерная переменная XYVAL 2ITER x 2ITER сетка точек, полученная из продукта тензора (XVAL, XVAL).
Положительный целочисленный ITER определяет количество вычисленных итераций и таким образом, улучшение приближений.
[S,W1,W2,W3,XYVAL] = wavefun2( вычисляет и также строит функции.'wname',ITER,'plot')
[S,W1,W2,W3,XYVAL] = wavefun2(, то, где wname,A,B)A и B являются положительными целыми числами, эквивалентно
[S,W1,W2,W3,XYVAL] = wavefun2(. Получившиеся функции построены. 'wname',max(A,B))
Когда A установлен равный специальному значению 0,
[S,W1,W2,W3,XYVAL] = wavefun2( эквивалентно 'wname',0)[S,W1,W2,W3,XYVAL] = wavefun2(.'wname',4,0)
[S,W1,W2,W3,XYVAL] = wavefun2( эквивалентно 'wname')[S,W1,W2,W3,XYVAL] = wavefun2(.'wname',4)
Выходные аргументы являются дополнительными.
Функция wavefun2 может только использоваться с ортогональным вейвлетом.
На следующем графике показывают линейную аппроксимацию вейвлета sym4, полученного с помощью каскадного алгоритма.
% Set number of iterations and wavelet name. iter = 4; wav = 'sym4'; % Compute approximations of the wavelet and scale functions using % the cascade algorithm and plot. [s,w1,w2,w3,xyval] = wavefun2(wav,iter,0);
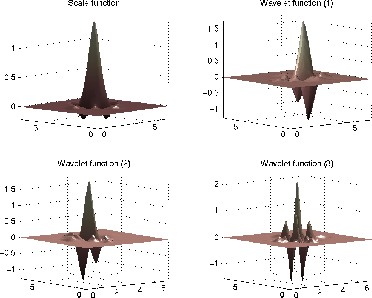
Смотрите wavefun для получения дополнительной информации.
Daubechies, я., Десять лекций по вейвлетам, CBMS, SIAM, 1992, стр 202Äì213.
Странг, Г.; Т. Нгуен (1996), вейвлеты и наборы фильтров, Wellesley-Кембриджское нажатие.