Оштрафованный порог для пакетного шумоподавления вейвлета
THR = wpbmpen(T,SIGMA,ALPHA)
wpbmpen(T,SIGMA,ALPHA,ARG)
THR = wpbmpen(T,SIGMA,ALPHA) возвращает глобальный порог THR для шумоподавления. THR получен пакетным содействующим правилом выбора вейвлета с помощью метода пенализации, предоставленного Birgé-Massart.
T является пакетным соответствием дерева вейвлета пакетному разложению вейвлета сигнала или изображения, чтобы быть denoised.
SIGMA является стандартным отклонением нулевого среднего Гауссова белого шума в модели шумоподавления (см. wnoisest для получения дополнительной информации).
ALPHA является настраивающимся параметром для термина штрафа. Это должно быть вещественное число, больше, чем 1. Разреженность пакетного представления вейвлета сигнала denoised или изображения растет с ALPHA. Обычно ALPHA = 2.
THR минимизирует оштрафованный критерий, данный
позвольте t* быть минимизатором
crit(t) = -sum(c(k)^2,k≤t) + 2*SIGMA^2*t*(ALPHA + log(n/t))
где c(k) является пакетными коэффициентами вейвлета, отсортированными в порядке убывания их абсолютного значения, и n является количеством коэффициентов, затем THR = | c (t*) |.
wpbmpen(T,SIGMA,ALPHA,ARG) вычисляет глобальный порог и, кроме того, строит три кривые:
2*SIGMA^2*t*(ALPHA + log(n/t))
sum(c(k)^2,k£t)
crit(t)
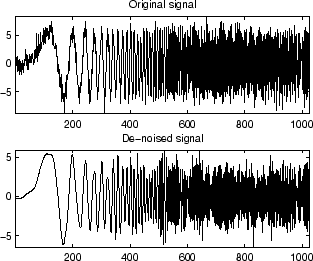
% Example 1: Signal denoising.
% Load noisy chirp signal.
load noischir; x = noischir;
% Perform a wavelet packet decomposition of the signal
% at level 5 using sym6.
wname = 'sym6'; lev = 5;
tree = wpdec(x,lev,wname);
% Estimate the noise standard deviation from the
% detail coefficients at level 1,
% corresponding to the node index 2.
det1 = wpcoef(tree,2);
sigma = median(abs(det1))/0.6745;
% Use wpbmpen for selecting global threshold
% for signal denoising, using the recommended parameter.
alpha = 2;
thr = wpbmpen(tree,sigma,alpha)
thr =
4.5740
% Use wpdencmp for denoising the signal using the above
% threshold with soft thresholding and keeping the
% approximation.
keepapp = 1;
xd = wpdencmp(tree,'s','nobest',thr,keepapp);
% Plot original and denoised signals.
figure(1)
subplot(211), plot(x),
title('Original signal')
subplot(212), plot(xd)
title('De-noised signal')
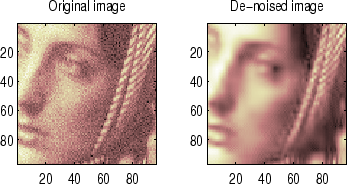
% Example 2: Image denoising.
% Load original image.
load noiswom;
nbc = size(map,1);
% Perform a wavelet packet decomposition of the image
% at level 3 using coif2.
wname = 'coif2'; lev = 3;
tree = wpdec2(X,lev,wname);
% Estimate the noise standard deviation from the
% detail coefficients at level 1.
det1 = [wpcoef(tree,2) wpcoef(tree,3) wpcoef(tree,4)];
sigma = median(abs(det1(:)))/0.6745;
% Use wpbmpen for selecting global threshold
% for image denoising.
alpha = 1.1;
thr = wpbmpen(tree,sigma,alpha)
thr =
38.5125
% Use wpdencmp for denoising the image using the above
% thresholds with soft thresholding and keeping the
% approximation.
keepapp = 1;
xd = wpdencmp(tree,'s','nobest',thr,keepapp);
% Plot original and denoised images.
figure(2)
colormap(pink(nbc));
subplot(221), image(wcodemat(X,nbc))
title('Original image')
subplot(222), image(wcodemat(xd,nbc))
title('De-noised image')