Exponenta Banner

allmargin

Запас по амплитуде, запас по фазе, задерживает поле и частоты среза

свернуть все на странице

Синтаксис

S = allmargin(L)
S = allmargin(mag,phase,w,ts)

Описание

пример

S = allmargin(L) вычисляет запас по амплитуде, запас по фазе, поле задержки и соответствующие частоты среза для SISO или цикла отрицательной обратной связи MIMO с ответом разомкнутого цикла L. Цикл отрицательной обратной связи вычисляется как feedback(L,eye(M)), где M количество вводов и выводов в L.

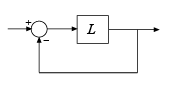
Для системы MIMO, allmargin возвращает цикл за один раз запасы устойчивости для системы замкнутого цикла отрицательной обратной связи. Используйте allmargin найти классические поля любой модели SISO или MIMO, включая модели с задержками.

пример

S = allmargin(mag,phase,w,ts) вычисляет запасы устойчивости из данных о частотной характеристике mag, phaseW, и шаг расчета, ts.

Примеры

свернуть все

Скрипт Open Live Script

В данном примере считайте передаточную функцию разомкнутого цикла SISO L данный,

L=25s3+10s2+10s+10

L = tf(25,[1 10 10 10]);

Найдите запасы устойчивости L.

S = allmargin(L)
S = struct with fields:
     GainMargin: 3.6000
    GMFrequency: 3.1623
    PhaseMargin: 29.1104
    PMFrequency: 1.7844
    DelayMargin: 0.2847
    DMFrequency: 1.7844
         Stable: 1

Выход S структура с классическими полями и их соответствующими частотами среза цикла отрицательной обратной связи L.

Скрипт Open Live Script

В данном примере считайте модель в пространстве состояний MIMO L с 2 входными параметрами и 2 выходными параметрами.

Загрузите данные.

load('mimoStateSpaceModel.mat','L')

Найдите классические поля для системы MIMO.

S = allmargin(L)
S=2×7 struct
    GainMargin
    GMFrequency
    PhaseMargin
    PMFrequency
    DelayMargin
    DMFrequency
    Stable

Выход S 2 1 массив структур классических полей и их соответствующих частот среза. Например, S(1) относится к запасам устойчивости первого канала обратной связи ввода-вывода со всеми другими замкнутыми кругами.

Скрипт Open Live Script

В данном примере загрузите invertedPendulumArray.mat, который содержит массив 3х3 инвертированных моделей SISO маятника. Масса маятника варьируется, когда вы перемещаетесь от модели до модели вдоль отдельного столбца sys, и длина маятника варьируется, когда вы проходите одна строка. Массовые используемые значения составляют 100 г, 200 г и 300 г, и используемые длины маятника составляют 3 м, 2 м и 1 м соответственно.

Column1Column2Column3Row1100g,3m100g,2m100g,1mRow2200g,3m200g,2m200g,1mRow3300g,3m300g,2m300g,1m

load('invertedPendulumArray.mat','sys');
size(sys)
3x3 array of transfer functions.
Each model has 1 outputs and 1 inputs.

Найдите запасы устойчивости для всех моделей в массиве.

S = allmargin(sys)
S=3×3 struct
    GainMargin
    GMFrequency
    PhaseMargin
    PMFrequency
    DelayMargin
    DMFrequency
    Stable

allmargin возвращает 3х3 массив структур S, в котором каждая запись является структурой, содержащей запасы устойчивости соответствующей записи в sys. Например, запасы устойчивости модели с 100-граммовым весом маятника и 2 м длиной содержатся в S(1,2).

Скрипт Open Live Script

В данном примере загрузите данные о частотной характеристике системы разомкнутого цикла, состоя из величин m и значения фазы p измеренный на частотах в w.

load('openLoopFRData.mat','m','p','w','ts');

Вычислите запасы устойчивости с помощью данных о частотной характеристике.

S = allmargin(m,p,w,ts)
S = struct with fields:
     GainMargin: 0.6249
    GMFrequency: 1.2732
    PhaseMargin: [-90.0000 48.9853]
    PMFrequency: [1.0000 1.5197]
    DelayMargin: [4.7124 0.5626]
    DMFrequency: [1.0000 1.5197]
         Stable: NaN

Выход S структура с классическими полями и их соответствующими частотами среза. Начиная с allmargin не может оценить устойчивость для моделей данных частотной характеристики, S.Stable = NaN.

Входные параметры

свернуть все

Ответ разомкнутого цикла, заданный как модель динамической системы. L может быть SISO или MIMO, пока это имеет то же количество вводов и выводов. allmargin вычисляет классические запасы устойчивости для отрицательной обратной связи система с обратной связью feedback(L,eye(M)):

Вычислить запасы устойчивости системы положительной обратной связи feedback(L,eye(M),+1), используйте allmargin(-L).

Когда у вас есть контроллер P и объект C, можно вычислить запасы устойчивости для усиления и изменений фазы при вводах или выводах объекта. Из следующей схемы:

  • Чтобы вычислить поля на объекте выходные параметры, установите L = P*C.

  • Чтобы вычислить поля во входных параметрах объекта, установите L = C*P.

L может быть непрерывное время или дискретное время. Если L обобщенная модель в пространстве состояний (genss или uss), затем allmargin использует текущее значение или номинальную стоимость всех блоков системы управления в L.

Если L модель данных частотной характеристики (такая как frd), затем allmargin вычисляет поля на каждой частоте, представленной в модели. Функция возвращает поля на частоте с самым маленьким запасом устойчивости.

Если L массив моделей, затем allmargin вычисляет поля для каждой модели в массиве.

Величина отклика системы в абсолютных единицах, заданных как трехмерный массив. mag M массивом m на n, где M является количеством вводов или выводов, и N является количеством точек частоты. Для получения дополнительной информации о получении mag, смотрите Получают Данные о Величине и Фазе и Величину и Фазу Системы MIMO.

Фаза отклика системы в градусах, заданный как трехмерный массив. phase M массивом m на n, где M является количеством вводов или выводов, и N является количеством точек частоты. Для получения дополнительной информации о получении phase, смотрите Получают Данные о Величине и Фазе и Величину и Фазу Системы MIMO.

Частоты, на которых получены величина и значения фазы отклика системы, задали как вектор-столбец. Можно предоставить вектору частоты w в любых модулях; allmargin возвращает частоты в тех же модулях. allmargin интерполирует между точками частоты, чтобы аппроксимировать истинные запасы устойчивости.

Шаг расчета, заданный как целое число. allmargin использование ts найти запасы устойчивости из данных о частотной характеристике.

  • Для моделей непрерывного времени, набор ts = 0.

  • Для моделей дискретного времени, ts положительное целое число, представляющее период выборки. Чтобы обозначить модель дискретного времени с незаданным шагом расчета, установите ts = -1.

Выходные аргументы

свернуть все

Усиление, фаза, и поля задержки, возвратилось как массив структур.

Выход S структура со следующими полями:

  • GMFrequency: Все-180 ° (360 ° по модулю) частоты среза в rad/TimeUnit, где TimeUnit единицы измерения времени, заданные в TimeUnit свойство L.

  • GainMargin: Соответствующие запасы по амплитуде, заданные как 1/G, где G усиление в частоте среза на-180 °. Запасы по амплитуде находятся в абсолютных единицах.

  • PMFrequency: Все частоты среза на 0 дБ в rad/TimeUnit, где TimeUnit единицы измерения времени, заданные в TimeUnit свойство L.

  • PhaseMargin: Соответствующие запасы по фазе в градусах.

  • DMFrequency и DelayMargin: DelayMargin максимальная сумма задержки, которую может терпеть система, прежде чем это потеряет устойчивость. DMFrequency содержит критические частоты, соответствующие полям задержки. Задержитесь поля заданы в единицах измерения времени системы для систем непрерывного времени и множителей шага расчета для систем дискретного времени.

  • Stable: 1 если номинальная система с обратной связью устойчива, 0 если нестабильный, и NaN если устойчивость не может быть оценена. В общем случае allmargin не может оценить устойчивость frd система.

Когда L M-by-M система MIMO, S массив структур M-1. Например, S(j) дает запасы устойчивости для j-th канала обратной связи со всеми другими замкнутыми кругами (один цикл за один раз поля).

Советы

  • allmargin принимает что система с ответом разомкнутого цикла L система отрицательной обратной связи. Вычислить классические запасы устойчивости системы положительной обратной связи feedback(L,eye(M),+1), используйте allmargin(-L).

  • Чтобы вычислить классические поля для системы, смоделированной в Simulink®, сначала линеаризуйте модель, чтобы получить ответ разомкнутого цикла в конкретной рабочей точке. Затем используйте allmargin вычислить классические запасы устойчивости для линеаризованной системы. Для получения дополнительной информации смотрите Запасы устойчивости Модели Simulink (Robust Control Toolbox).

Смотрите также

| |

Темы

Представлено до R2006a

Документация Control System Toolbox
Поддержка