hwcalbycap

Калибруйте Белое как оболочка дерево с помощью дна

свернуть все на странице

Синтаксис

[Alpha,Sigma,OptimOut] = hwcalbycap(RateSpec,MarketStrikeMarketMaturity,MarketVolatility)
[Alpha,Sigma,OptimOut = hwcalbycap(RateSpec,MarketStrikeMarketMaturity,MarketVolatility,Strike,Settle,Maturity)
[Alpha,Sigma,OptimOut] = hwcalbycap(___,Name,Value)

Описание

пример

[Alpha,Sigma,OptimOut] = hwcalbycap(RateSpec,MarketStrikeMarketMaturity,MarketVolatility) калибрует Alpha (возвращение к среднему уровню) и Sigma (энергозависимость) с помощью данных о рынке дна и модели Hull-White с помощью целой поверхности дна.

Белые как оболочка калибровочные функции (hwcalbycap и hwcalbyfloor) поддержка три модели: Черный (значение по умолчанию), Bachelier или Normal и Переключенный Черный цвет. Для получения дополнительной информации смотрите дополнительные аргументы для Shift и Model.

пример

[Alpha,Sigma,OptimOut = hwcalbycap(RateSpec,MarketStrikeMarketMaturity,MarketVolatility,Strike,Settle,Maturity) оценивает Alpha (возвращение к среднему уровню) и Sigma (энергозависимость) с помощью данных о рынке дна и модели Hull-White, чтобы оценить дно в конкретной зрелости/энергозависимости с помощью дополнительных дополнительных входных параметров в Strike, Settle, и Maturity.

Strike, Settle, и Maturity аргументы заданы, чтобы калибровать к отдельному моменту на поверхности волатильности рынка. Если не использовано, калибровка выполняется через все инструменты рынка

Для примера калибровки использования модели Hull-White с Strike, Settle, и Maturity входные параметры, см., что Калибрующая Белая как оболочка Модель Использует Данные о Рынке.

пример

[Alpha,Sigma,OptimOut] = hwcalbycap(___,Name,Value) добавляют дополнительные аргументы пары "имя-значение".

Примеры

свернуть все

В этом примере показано, как использовать hwcalbycap входные параметры для MarketStrike, MarketMaturity, и MarketVolatility калибровать модель HW с помощью целой поверхности энергозависимости дна.

Данные о волатильности рынка дна, покрывающие две забастовки более чем 12 дат погашения.

Reset = 4;
MarketStrike = [0.0590; 0.0790];

MarketMaturity = {'21-Mar-2008'; '21-Jun-2008'; '21-Sep-2008'; '21-Dec-2008';
    '21-Mar-2009'; '21-Jun-2009'; '21-Sep-2009'; '21-Dec-2009';
    '21-Mar-2010'; '21-Jun-2010'; '21-Sep-2010'; '21-Dec-2010'};
MarketMaturity = datenum(MarketMaturity);

MarketVolaltility = [0.1533 0.1731 0.1727 0.1752 0.1809 0.1800 0.1805 0.1802...
    0.1735 0.1757 0.1755 0.1755;
    0.1526 0.1730 0.1726 0.1747 0.1808 0.1792 0.1797 0.1794...
    0.1733 0.1751 0.1750 0.1745];

Постройте поверхность волатильности рынка.

[AllMaturities,AllStrikes] = meshgrid(MarketMaturity,MarketStrike);
figure;
surf(AllMaturities,AllStrikes,MarketVolaltility)
datetick
xlabel('Maturity')
ylabel('Strike')
zlabel('Volatility')
title('Market Volatility Data')

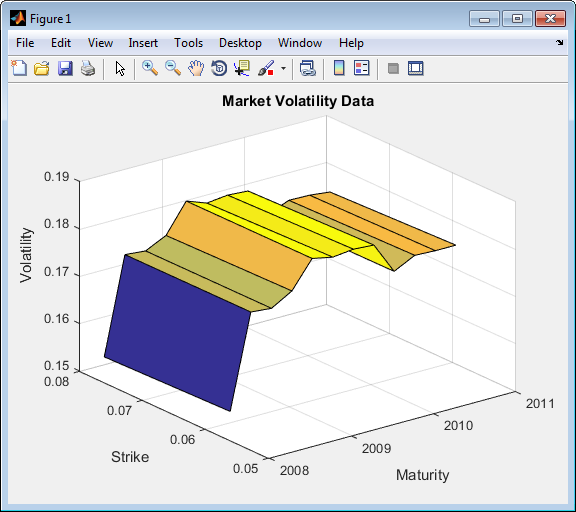
Установите структуру термина процентной ставки и создайте RateSpec.

Settle = '21-Jan-2008';
Compounding = 4;
Basis = 0;
Rates= [0.0627; 0.0657; 0.0691; 0.0717; 0.0739; 0.0755; 0.0765; 0.0772;
    0.0779; 0.0783; 0.0786; 0.0789];
EndDates = {'21-Mar-2008';'21-Jun-2008';'21-Sep-2008';'21-Dec-2008';...
    '21-Mar-2009';'21-Jun-2009';'21-Sep-2009';'21-Dec-2009';....
    '21-Mar-2010';'21-Jun-2010';'21-Sep-2010';'21-Dec-2010'};
RateSpec = intenvset('ValuationDate', Settle, 'StartDates', Settle,...
    'EndDates', EndDates,'Rates', Rates, 'Compounding', Compounding,...
    'Basis',Basis)

RateSpec = 

           FinObj: 'RateSpec'
      Compounding: 4
             Disc: [12x1 double]
            Rates: [12x1 double]
         EndTimes: [12x1 double]
       StartTimes: [12x1 double]
         EndDates: [12x1 double]
       StartDates: 733428
    ValuationDate: 733428
            Basis: 0
     EndMonthRule: 1

Калибруйте модель Hull-White из данных о рынке.

o = optimoptions('lsqnonlin','TolFun',1e-5,'Display','off');

[Alpha, Sigma] = hwcalbycap(RateSpec, MarketStrike, MarketMaturity,...
    MarketVolaltility, 'Reset', Reset,'Basis', Basis, 'OptimOptions', o)
Warning: LSQNONLIN did not converge to an optimal solution. It exited with exitflag = 3.
 
> In hwcalbycapfloor>optimizeOverCapSurface at 232
  In hwcalbycapfloor at 79
  In hwcalbycap at 81 

Alpha =

    0.0943


Sigma =

    0.0146

Сравните с Черными ценами.

BlkPrices = capbyblk(RateSpec,AllStrikes(:), Settle, AllMaturities(:),...
    MarketVolaltility(:),'Reset',Reset,'Basis',Basis);
BlkPrices =

    0.0604
         0
    0.2729
    0.0006
    0.6498
    0.0412
    1.1121
    0.1426
    1.6426
    0.3131
    2.1869
    0.4998
    2.7056
    0.6894
    3.2124
    0.8815
    3.7311
    1.0686
    4.2246
    1.2790
    4.7027
    1.4810
    5.1877
    1.6919

Setup Белое как оболочка дерево с помощью калиброванных параметров, альфы и сигмы.

VolDates    = EndDates;
VolCurve    = Sigma*ones(numel(EndDates),1);
AlphaDates  = EndDates;
AlphaCurve  = Alpha*ones(numel(EndDates),1);
HWVolSpec   = hwvolspec(Settle, VolDates, VolCurve, AlphaDates, AlphaCurve);

HWTimeSpec  = hwtimespec(Settle, EndDates, Compounding);
HWTree = hwtree(HWVolSpec, RateSpec, HWTimeSpec, 'Method', 'HW2000')

HWTree = 

      FinObj: 'HWFwdTree'
     VolSpec: [1x1 struct]
    TimeSpec: [1x1 struct]
    RateSpec: [1x1 struct]
        tObs: [0 0.6593 1.6612 2.6593 3.6612 4.6593 5.6612 6.6593 7.6612 8.6593 9.6612 10.6593]
        dObs: [733428 733488 733580 733672 733763 733853 733945 734037 734128 734218 734310 734402]
      CFlowT: {1x12 cell}
       Probs: {1x11 cell}
     Connect: {1x11 cell}
     FwdTree: {1x12 cell}

Вычислите Белые как оболочка цены на основе калиброванного дерева.

HWPrices = capbyhw(HWTree, AllStrikes(:), Settle, AllMaturities(:), Reset, Basis)
HWPrices =

    0.0601
         0
    0.2788
         0
    0.6580
    0.0518
    1.1254
    0.1485
    1.6591
    0.3123
    2.2076
    0.5022
    2.7319
    0.6883
    3.2459
    0.8774
    3.7771
    1.0900
    4.2769
    1.2875
    4.7645
    1.4845
    5.2572
    1.6921

Постройте Черные цены против калиброванных Белых как оболочка древовидных цен.

figure;
plot(AllMaturities(:), BlkPrices, 'or', AllMaturities(:), HWPrices, '*b');
datetick('x', 2)
xlabel('Maturity');
ylabel('Price');
title('Black and Calibrated (HW) Prices');
legend('Black Price', 'Calibrated HW Tree Price','Location', 'NorthWest');
grid on

Скрипт Open Live Script

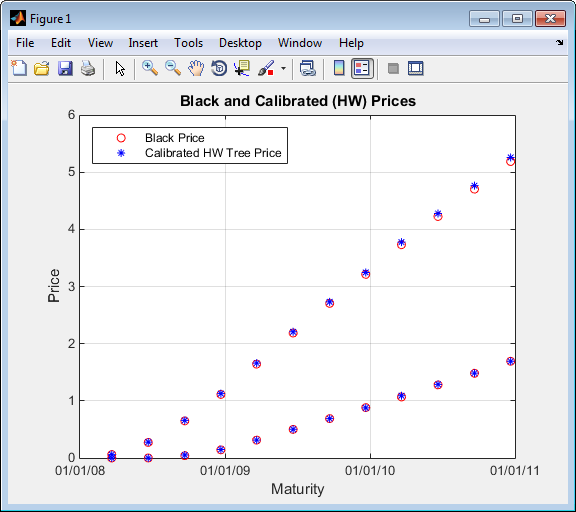
В этом примере показано, как использовать hwcalbycap калибровать данные о рынке с моделью Normal (Bachelier) к цене caplets. Используйте модель Normal (Bachelier), чтобы выполнить калибровки при работе с отрицательными процентными ставками, забастовками и нормальной подразумеваемой волатильностью.

Рассмотрите дно этими параметрами:

Settle = 'Dec-30-2016';
Maturity = 'Dec-30-2019';
Strike = -0.001075;
Reset = 2;
Principal = 100;
Basis = 0;

caplets и данные о рынке для этого примера заданы как:

capletDates = cfdates(Settle, Maturity, Reset, Basis);
datestr(capletDates')
ans = 6x11 char array
    '30-Jun-2017'
    '30-Dec-2017'
    '30-Jun-2018'
    '30-Dec-2018'
    '30-Jun-2019'
    '30-Dec-2019'


% Market data information
MarketStrike = [-0.0013; 0];
MarketMat =  {'30-Jun-2017';'30-Dec-2017';'30-Jun-2018'; '30-Dec-2018';'30-Jun-2019'; '30-Dec-2019'};
MarketVol = [0.184 0.2329 0.2398 0.2467 0.2906 0.3348;   % First row in table corresponding to Strike 1 
             0.217 0.2707 0.2760 0.2814 0.3160 0.3508];  % Second row in table corresponding to Strike 2

Задайте RateSpec.

Rates= [-0.002210;-0.002020;-0.00182;-0.001343;-0.001075];
ValuationDate = 'Dec-30-2016';
EndDates = {'30-Jun-2017';'Dec-30-2017';'30-Jun-2018';'Dec-30-2018';'Dec-30-2019'};
Compounding = 2;
Basis = 0;

RateSpec = intenvset('ValuationDate', ValuationDate, ...
'StartDates', ValuationDate, 'EndDates', EndDates, ...
'Rates', Rates, 'Compounding', Compounding, 'Basis', Basis);

Используйте hwcalbycap найти значения для параметров энергозависимости Alpha и Sigma использование модели Normal (Bachelier).

format short
o=optimoptions('lsqnonlin','TolFun',100*eps);
warning ('off','fininst:hwcalbycapfloor:NoConverge')
[Alpha, Sigma, OptimOut] = hwcalbycap(RateSpec, MarketStrike, MarketMat,...
MarketVol, Strike, Settle, Maturity, 'Reset', Reset, 'Principal', Principal,...
'Basis', Basis, 'OptimOptions', o, 'model', 'normal')
Local minimum possible.
lsqnonlin stopped because the size of the current step is less than
the value of the step size tolerance.

Alpha = 1.0000e-06

Sigma = 0.3384

OptimOut = struct with fields:
     resnorm: 1.5181e-04
    residual: [5x1 double]
    exitflag: 2
      output: [1x1 struct]
      lambda: [1x1 struct]
    jacobian: [5x2 double]

OptimOut.residual поле OptimOut структура является невязкой оптимизации. Это значение содержит различие между Нормальным (Bachelier) caplets и вычисленными во время оптимизации. Используйте OptimOut.residual значение, чтобы вычислить percentual различие (ошибка) по сравнению с Нормальным (Bachelier) caplet цены, и затем решить, приемлема ли невязка. Существует почти всегда некоторая невязка, поэтому решите, приемлемо ли параметризовать рынок с одним значением Alpha и Sigma.

Оцените caplets использование данных о рынке и модели Normal (Bachelier), чтобы получить ссылку caplet значения. Чтобы определить эффективность оптимизации, вычислите ссылку caplet значения с помощью Нормальной формулы (Bachelier) и данных о рынке. Отметьте, необходимо сначала интерполировать данные о рынке, чтобы получить caplets для вычисления.

MarketMatNum = datenum(MarketMat);
[Mats, Strikes] = meshgrid(MarketMatNum, MarketStrike);
FlatVol = interp2(Mats, Strikes, MarketVol, datenum(Maturity), Strike, 'spline');

[CapPrice, Caplets] = capbynormal(RateSpec, Strike, Settle, Maturity, FlatVol,...
'Reset', Reset, 'Basis', Basis, 'Principal', Principal); 
Caplets = Caplets(2:end)'
Caplets = 5×1

    4.7392
    6.7799
    8.2609
    9.6136
   10.6455

Сравните оптимизированные значения и Нормальные значения (Bachelier), и отобразите результаты графически. После вычисления ссылочных значений для caplets сравните значения аналитически и графически определить ли расчетные одно значения Alpha и Sigma обеспечьте соответствующее приближение.

OptimCaplets = Caplets+OptimOut.residual;

disp('   ');
   

disp(' Bachelier   Calibrated Caplets');
 Bachelier   Calibrated Caplets

disp([Caplets        OptimCaplets])
    4.7392    4.7453
    6.7799    6.7851
    8.2609    8.2657
    9.6136    9.6112
   10.6455   10.6379

plot(MarketMatNum(2:end), Caplets, 'or', MarketMatNum(2:end), OptimCaplets, '*b');
datetick('x', 2)
xlabel('Caplet Maturity');
ylabel('Caplet Price');
ylim ([0 16]);
title('Bachelier and Calibrated Caplets');
h = legend('Bachelier Caplets', 'Calibrated Caplets');
set(h, 'color', [0.9 0.9 0.9]);
set(h, 'Location', 'SouthEast');
set(gcf, 'NumberTitle', 'off')
grid on

Входные параметры

свернуть все

Спецификация процентной ставки для начальной кривой уровня, заданной RateSpec полученный из intenvset. Для получения информации о спецификации процентной ставки смотрите intenvset.

Типы данных: struct

Забастовка рыночной капитализации, заданная как NINST- 1 вектор.

Типы данных: double

Даты погашения рыночной капитализации, заданные как NINST- 1 вектор.

Типы данных: double

Рынок плоские колебания, заданные как NSTRIKES- NMATS матрица рынка плоские колебания, где NSTRIKES количество забастовок caplet от MarketStrike и NMATS caplet даты погашения от MarketMaturity.

Типы данных: double

(Необязательно) Уровень, на котором осуществлено дно, задал как десятичное скалярное значение.

Типы данных: single

(Необязательно) Расчетный день дна, заданного как скалярный последовательный номер даты или символ даты.

Типы данных: single | char

(дополнительная) Дата погашения дна, заданного как скалярный последовательный номер даты или вектор символов даты.

Типы данных: single | char

Аргументы в виде пар имя-значение

Задайте дополнительные разделенные запятой пары Name,Value аргументы. Name имя аргумента и Value соответствующее значение. Name должен появиться в кавычках. Вы можете задать несколько аргументов в виде пар имен и значений в любом порядке, например: Name1, Value1, ..., NameN, ValueN.

Пример: [Alpha,Sigma,OptimOut] = hwcalbycap(RateSpec,MarketStrike,MarketMaturity,MarketVolaltility,'Reset',2,'Principal',100000,'Basis',3,'OptimOptions',o)

Частота платежей в год, заданный как разделенная запятой пара, состоящая из 'Reset' и скалярное числовое значение.

Типы данных: double

Отвлеченная основная сумма, заданная как разделенная запятой пара, состоящая из 'Principal' и скалярное неотрицательное целое число.

Типы данных: single

Основание дневного количества, используемое при пересчитывании на год входного форвардного курса, заданного как разделенная запятой пара, состоящая из 'Basis' и скалярное значение. Значения:

  •  0 = фактический/фактический

  •  1 = 30/360 (СИА)

  •  2 = Фактический/360

  •  3 = Фактический/365

  •  4 = 30/360 (PSA)

  •  5 = 30/360 (ISDA)

  •  6 = 30/360 (европеец)

  •  7 = Фактический/365 (японский язык)

  •  8 = фактический/фактический (ICMA)

  •  9 = Фактический/360 (ICMA)

  •  10 = Фактический/365 (ICMA)

  •  11 = 30/360E (ICMA)

  •  12 = Фактический/365 (ISDA)

  •  13 = ШИНА/252

Для получения дополнительной информации смотрите Основание.

Типы данных: single

Нижние границы, заданные как разделенная запятой пара, состоящая из 'LB' и 2- 1 вектор нижних границ, заданных как [LBSigma; LBAlpha], используемый в функции алгоритма поиска. Для получения дополнительной информации смотрите lsqnonlin.

Типы данных: double

Верхние границы, заданные как разделенная запятой пара, состоящая из 'UB' и 2- 1 вектор верхних границ, заданных как [UBSigma; LBAlpha], используемый в функции алгоритма поиска. Для получения дополнительной информации смотрите lsqnonlin.

Типы данных: double

Начальные значения, заданные как разделенная запятой пара, состоящая из 'XO' и 2- 1 вектор начальных значений, заданных как [Sigma0; Alpha0], используемый в функции алгоритма поиска. Для получения дополнительной информации смотрите lsqnonlin.

Типы данных: double

Параметры оптимизации, заданные как разделенная запятой пара, состоящая из 'OptimOptions' и структура задана при помощи optimoptions.

Типы данных: struct

Переключите десятичные числа на нижний регистр для переключенной модели Black, заданной как разделенная запятой пара, состоящая из 'Shift' и скалярное положительное десятичное значение. Установите этот параметр на положительный сдвиг в десятичных числах, чтобы добавить положительный сдвиг на форвардный курс и Strike, который эффективно устанавливает отрицательную нижнюю границу для форвардного курса и Strike. Например, Shift значение 0.01 равно 1%-му сдвигу.

Типы данных: single

Индикатор для модели, используемой в калибровочной стандартной программе, заданной как разделенная запятой пара, состоящая из 'Model' и скалярный вектор символов со значением normal или lognormal.

Типы данных: char

Выходные аргументы

свернуть все

Значение возвращения к среднему уровню, полученное из калибровки дна с помощью информации о рынке, возвращенной как скалярное значение.

Значение энергозависимости, полученное из калибровки дна с помощью информации о рынке, возвращенной как скаляр.

Результаты оптимизации, возвращенные как структура.

Смотрите также

| | | |

Темы

Представленный в R2009a

Документация Financial Instruments Toolbox
Поддержка
Для просмотра документации необходимо авторизоваться на сайте