Введение в методы присвоения в системах слежения

Фон

В цели кратного, отслеживающей (MTT) система, один или несколько датчиков генерируют несколько обнаружений от нескольких целей на сканировании. Чтобы отследить эти цели, один существенный шаг должен присвоить эти обнаружения правильно целям или отслеживает обеспеченный в средстве отслеживания так, чтобы эти обнаружения могли использоваться, чтобы обновить эти дорожки. Если количество целей или обнаружений является большим, или между различными гипотезами присвоения существуют конфликты, присвоение обнаружений сложно.

В зависимости от размерности присвоения проблемы присвоения могут быть категоризированы в:

2D проблема присвоения – присваивает цели n наблюдениям m. Например, присвойте 5 дорожек 6 обнаружениям, сгенерированным от одного датчика, когда-то продвигаются.
Проблема присвоения S-D – присваивает цели n набору (m ₁, m ₂, m ₃, …) наблюдений. Например, присвойте 5 дорожек 6 обнаружениям от одного датчика и 4 обнаружениям от другого датчика одновременно. Этим примером является типичная 3-D проблема присвоения.

Чтобы проиллюстрировать основную идею о проблеме присвоения, рассмотрите простой 2D пример присвоения. Одна компания пытается присвоить 3 задания 3 рабочим. Из-за различных уровней опыта рабочих не все рабочие могут завершить каждое задание с той же эффективностью. Стоимость (в часах) каждого рабочего, чтобы закончить каждое задание дана матрицей стоимости, показанной в таблице. Правило присвоения состоит в том, что каждый рабочий может только устроиться на одну работу, и на одну работу может только устроиться один рабочий. Чтобы гарантировать КПД, объект этого присвоения состоит в том, чтобы минимизировать общую стоимость.

Рабочий	Задание
Рабочий	1	2	3
1	41	72	39
2	22	29	49
3	27	39	60

Поскольку количества рабочих и заданий являются оба маленькими в этом примере, все возможные присвоения могут быть получены перечислением, и минимальное экономичное решение подсвечено в таблице с парами присвоения (1, 3), (2, 2) и (3, 1). На практике, когда размер присвоения становится больше, оптимальное решение затрудняет, чтобы получить для 2D присвоения. Для проблемы присвоения S-D оптимальное решение не может быть доступным на практике.

2D присвоение в нескольких предназначается для отслеживания

В 2D проблеме присвоения MTT средство отслеживания пытается присвоить несколько дорожек нескольким обнаружениям. Кроме упомянутой выше проблемы размерности, несколько других факторов могут значительно изменить сложность присвоения:

Распределение цели или обнаружения — Если цели редко распределяются, сопоставляя цель к ее соответствующему обнаружению, относительно легко. Однако, если цели или обнаружения плотно распределяются, присвоения становятся неоднозначными, потому что присвоение цели к обнаружению или другому соседнему обнаружению редко имеет любые значения на стоимости.
Вероятность обнаружения (P _d) датчика — P _d описывает вероятность, что цель обнаруживается датчиком, если цель в поле зрения датчика. Если P _d датчика мал, то истинная цель не может дать начало никакому обнаружению во время сканирования датчика. В результате дорожка, представленная истинной целью, может украсть обнаружения из других дорожек.
Разрешение датчика — разрешение Датчика определяет способность датчика отличить обнаружения от двух целей. Если разрешение датчика является низким, то две цели в близости могут только дать начало одному обнаружению. Это нарушает общее предположение, что каждое обнаружение может только быть присвоено одной дорожке и результатам в неразрешимых конфликтах присвоения между дорожками.
Помеха или ложный сигнальный уровень датчика — Ложные предупреждения вводят дополнительные возможные присвоения и поэтому увеличивают сложность присвоения данных.

Сложность задачи присвоения может определить который методы присвоения применяться. В тулбоксе Sensor Fusion and Tracking Toolbox™ три 2D подхода присвоения используются, соответствуя трем различным средствам отслеживания:

trackerGNN — принимает глобальный самый близкий подход присвоения данных
trackerJPDA — принимает объединенный подход ассоциации данных о вероятности
trackerTOMHT — принимает ориентированный на средство отслеживания несколько гипотеза, отслеживающая подход

Обратите внимание на то, что каждое средство отслеживания обрабатывает данные от датчиков последовательно, означая, что каждое средство отслеживания только имеет дело с проблемой присвоения с обнаружениями одного датчика за один раз. Даже с этой обработкой, может все еще быть слишком много пар присвоения. Чтобы сократить количество дорожки и пар обнаружения, рассмотренных для присвоения, метод пропускания часто используется.

Пропускание

Пропускание является механизмом экранирования, чтобы определить, какие наблюдения являются допустимыми кандидатами, чтобы обновить существующие дорожки и устранить маловероятные пары обнаружения к дорожке с помощью информации о распределении предсказанных дорожек. Чтобы установить логический элемент валидации для дорожки на текущем сканировании, предполагаемая дорожка для текущего шага предсказана от предыдущего шага.

Например, средство отслеживания подтверждает дорожку во время t _k и получает несколько обнаружений во время t _{k +1}. Чтобы сформировать логический элемент валидации во время t _{k +1}, средство отслеживания сначала должно получить предсказанное измерение как:

${\hat{y}}_{k + 1} = h ({\hat{x}}_{k + 1 | k})$

где оценка дорожки предсказана со времени t _k и является моделью измерения, которая выводит ожидаемое измерение, учитывая состояние дорожки. Вектор невязок наблюдения

$\tilde{y} = y_{k + 1} - {\hat{y}}_{k + 1}$

где y _{k +1} является фактическим измерением. Чтобы установить контур логического элемента, ковариация невязки обнаружения, S используется, чтобы сформировать эллипсоидальный логический элемент валидации. Эллипсоидальный логический элемент, который устанавливает пространственную эллипсоидальную область на пробеле измерения, задан в расстоянии Mahalanobis как:

$d^{2} (y_{k + 1}) = {\tilde{y}}^{T} S^{- 1} \tilde{y} \leq G$

где G является порогом пропускания, который можно задать на основе требования присвоения. Увеличение порога может включить больше обнаружений в логический элемент.

После того, как логический элемент присвоения устанавливается для каждой дорожки, состояния пропускания каждого обнаружения y_{, i} (i = 1, …, n) может быть определен путем сравнения его расстояния Mahalanobis d ² (y _i) с порогом пропускания G. Если d ² (y _i) <G, то обнаружение y _i в логическом элементе дорожки и буду рассмотрена для ассоциации. В противном случае возможность обнаружения, сопоставленного с дорожкой, удалена. В рисунке 1 T ₁ представляет предсказанную оценку дорожки и O ₁ – O ₆ является шестью обнаружениями. На основе результата пропускания O ₁, O ₂, и O ₃ в логическом элементе валидации в фигуре.

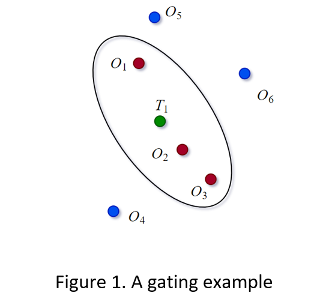
Метод Глобального самого близкого соседа (GNN)

Метод GNN является одним методом присвоения гипотезы. Для каждого нового набора данных цель состоит в том, чтобы присвоить глобальные самые близкие наблюдения существующим дорожкам и создать гипотезы нового трека для неприсвоенных обнаружений.

Задача присвоения GNN может быть легко решена, при отсутствии конфликтов ассоциации между дорожками. Средство отслеживания только должно присвоить дорожку своему самому близкому соседу. Однако конфликтные ситуации (см. рисунок 2) происходят, когда существует больше чем одно наблюдение в логическом элементе валидации дорожки, или наблюдение находится в логических элементах больше чем одной дорожки. Чтобы разрешить эти конфликты, средство отслеживания должно оценить матрицу стоимости.

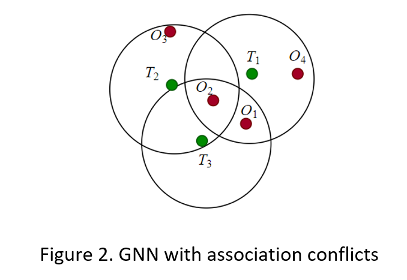
Элементы матрицы стоимости для метода GNN включают расстояние от дорожек до обнаружений и других факторов, которые вы можете хотеть рассмотреть. Например, один подход должен задать обобщенное статистическое расстояние между наблюдением j, чтобы отследить i как:

$C_{i j} = d_{i j} + \ln (| S_{i j} |)$

где d_{, ij} является расстоянием Mahalanobis и ln (|S_ij |), логарифм определителя остаточной ковариационной матрицы, используется, чтобы оштрафовать дорожки с большей неопределенностью прогноза.

Для проблемы присвоения, данной в рисунке 2, следующая таблица показывает гипотетическую матрицу стоимости. Непозволенные присвоения, которые провалили тест пропускания, обозначаются X. (На практике, затраты на непозволенные присвоения могут обозначаться большими значениями, такой как 1 000.)

Дорожки	Наблюдения
Дорожки	O ₁	O ₂	O ₃	O ₄
T1	9	6	X	6
T2	X	3	10	X
T2	8	4	X	X

Для этой проблемы подсвеченное оптимальное решение может быть найдено перечислением. O обнаружения ₃ является неприсвоенным, таким образом, средство отслеживания будет использовать его, чтобы создать новую предварительную дорожку. Для более сложных проблем присвоения GNN требуются более точные формулировки и более эффективные алгоритмы, чтобы получить оптимальное или субоптимальное решение.

Общая 2D проблема присвоения может быть сформирована как после. Учитывая элемент матрицы стоимости C _ij, найдите присвоение Z = {z _ij}, который минимизирует

$J = \sum_{i = 0}^{n} \sum_{j = 0}^{m} C_{i j} z_{i j}$

подвергните двум ограничениям:

$\begin{array}{l} \sum_{i = 0}^{m} z_{i j} = 1, \forall j \\ \sum_{j = 0}^{n} z_{i j} = 1, \forall i \end{array}$

Если дорожка i присвоена наблюдению j, то z _ij = 1. В противном случае, z _ij = 0. z _{i 0} = 1 представляет гипотезу, которые отслеживают i, не присвоен никакому обнаружению. Точно так же z _0j = 1 представляет гипотезу, что наблюдение j не присвоено никакой дорожке. Первое ограничение означает, что каждое обнаружение может быть присвоено не больше, чем одной дорожке. Второе ограничение означает, что каждая дорожка может быть присвоена не больше, чем одному обнаружению.

Sensor Fusion and Tracking Toolbox обеспечивает несколько функций, чтобы решить 2D задачи присвоения GNN:

assignmunkres – Использует алгоритм Munkres, который гарантирует оптимальное решение, но может потребовать большего количества операций вычисления.
assignauction – Использует аукционный алгоритм, который требует меньшего количества операций, но может возможно сходиться на оптимальном или субоптимальном решении.
assignjv – Использует алгоритм Шутника-Volgenant, который также сходится на оптимальном или субоптимальном решении, но обычно с более быстрой сходящейся скоростью.

В trackerGNN, можно выбрать алгоритм присвоения путем определения Assignment свойство.

K лучшие решения 2D проблемы присвоения

Из-за природы неопределенности проблем присвоения, только получая решение (оптимальный или субоптимальный) может не быть достаточным. Чтобы составлять несколько гипотез о присвоении между дорожками и обнаружениями, несколько субоптимальных решений требуются. Эти субоптимальные решения называются лучшими решениями K проблемы присвоения.

Лучшие решения K обычно получаются путем варьирования решения, полученного любой из ранее упомянутых функций присвоения. Затем на следующем шаге алгоритм лучшего решения K удаляет одну пару дорожки к обнаружению в исходном решении и находит следующее лучшее решение. Например, для этой матрицы стоимости:

$[\begin{matrix} 10 \\ 5897 & \times & 20 & \times \\ \begin{array}{l} \times \\ \times \end{array} & \begin{array}{l} 2115 \end{array} & \begin{array}{l} \times \\ 17 \end{array} & \begin{array}{l} \times \\ \times \end{array} \\ \times & \times & 16 & 22 \end{matrix}]$

каждая строка представляет стоимость, сопоставленную с дорожкой, и каждый столбец представляет стоимость, сопоставленную с обнаружением. Как подсвечено, оптимальное решение (7,15,16, 9) со стоимостью 47. На следующем шаге удалите первую пару (соответствие 7), и следующее лучшее решение (10,15, 20, 22) со стоимостью 67. После этого удалите вторую пару (соответствие 15), и следующее лучшее решение (7, 5,16, 9) со стоимостью 51. После нескольких шагов эти пять лучших решений:

Решение	Стоимость
(7,15,16, 9)	47
(7,5,17, 22)	51
(7,15, 8, 22)	52
(7, 21,16, 9)	53
(7, 21,17, 9)	53

Смотрите Находку Пять Лучших решений Используя пример Assignkbest, который использует assignkbest функционируйте, чтобы найти лучшие решения K.

Объединенная ассоциация данных о вероятности (JPDA) метод

В то время как метод GNN делает твердое присвоение из обнаружения к дорожке, метод JPDA применяет мягкое присвоение так, чтобы обнаружения в логическом элементе валидации дорожки могли все сделать взвешенные вклады в дорожку на основе их вероятности ассоциации.

Например, для результатов пропускания, показанных в рисунке 1, средство отслеживания JPDA вычисляет возможность ассоциации между дорожкой T ₁ и наблюдениями O ₁, O ₂, и O ₃. Примите, что вероятностью ассоциации этих трех наблюдений является p ₁₁, p ₁₂, и p ₁₃, и их остаточные значения относительно дорожки, которая T ₁, и, соответственно. Затем взвешенная сумма остаточных значений, сопоставленных с дорожкой T ₁:

${\tilde{y}}_{1} = \sum_{j = 1}^{3} p_{1 j} {\tilde{y}}_{1 j}$

В средстве отслеживания взвешенная невязка используется, чтобы обновиться, отслеживают T ₁ на шаге коррекции фильтра отслеживания. В фильтре вероятность неприсвоения, p ₁₀, также требуется, чтобы обновляться, отслеживают T ₁. Для получения дополнительной информации см. Алгоритм Коррекции JPDA для Дискретного Расширенного Фильтра Калмана.

Метод JPDA требует еще одного шага, когда существуют конфликты между присвоениями в различных дорожках. Например, в следующем рисунке, отследите T ₂ конфликта с T ₁ на присвоении наблюдения O ₃. Поэтому, чтобы вычислить вероятность ассоциации p ₁₃, объединенная вероятность, что T ₂ не присвоен O ₃ (который является T ₂, присвоен O ₆ или неприсвоенный) должна составляться.

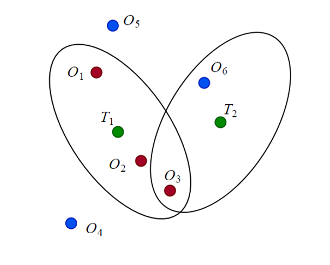
Метод Ориентированного на дорожку на несколько отслеживания гипотезы (TOMHT)

В отличие от метода JPDA, который комбинирует все обнаружения в логическом элементе валидации с помощью взвешенной суммы, метод TOMHT генерирует несколько гипотез или ветвей дорожек на основе обнаружений в логическом элементе и распространяет ветви высокой вероятности между шагами сканирования. После распространения эти гипотезы могут быть протестированы и сокращены на основе нового набора обнаружений.

Например, для сценария пропускания, показанного в рисунке 1, средство отслеживания TOMHT рассматривает следующие четыре гипотезы:

Не присвойте обнаружение T ₁ получившееся в гипотезе T ₁₀
Присвойте O ₁ T ₁ получившееся в гипотезе T ₁₁
Присвойте O ₂ T ₁ получившееся в гипотезе T ₁₂
Присвойте O ₃ T ₁ получившееся в гипотезе T ₁₃

Учитывая порог присвоения, средство отслеживания вычислит возможность каждой гипотезы и отбросит гипотезы с вероятностью ниже, чем порог. Гипотетически, если только p ₁₀ и p ₁₁ больше, чем порог, то только T ₁₀ и T ₁₁ распространен к следующему шагу для обновления обнаружения.

Присвоение S-D в нескольких предназначается для отслеживания

В проблеме присвоения S-D размерность присвоения S больше, чем 2. Обратите внимание на то, что все три средства отслеживания (trackerGNN, trackerJPDA, и trackerTOMHT) обнаружения процесса от каждого датчика последовательно, который приводит к 2D проблеме присвоения. Однако некоторые приложения требуют средства отслеживания, что процессы одновременные наблюдения от нескольких сканирований датчика целиком, который требует решения задачи присвоения S-D. Между тем присвоение S-D широко используется в отслеживании приложений, таких как статический сплав данных, который предварительно обрабатывает данные об обнаружении, прежде чем питается средство отслеживания.

Проблема присвоения S-D для статического сплава данных имеет сканирования S области наблюдения от нескольких датчиков одновременно, и каждое сканирование состоит из нескольких обнаружений. Источники обнаружения могут быть действительными целями или ложными предупреждениями. Объект состоит в том, чтобы обнаружить неизвестное количество целей и оценить их состояния. Например, как показано в рисунке 4, три сканирования датчика производят шесть обнаружений. Обнаружения в том же цвете принадлежат тому же сканированию. Поскольку каждое сканирование генерирует два обнаружения, существует, вероятно, две цели в области наблюдения. Чтобы выбрать между различным присвоением или возможностями ассоциации, оцените матрицу стоимости.

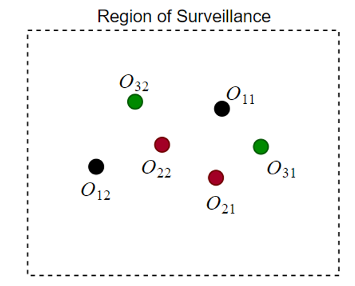
Вычисление стоимости может зависеть от многих факторов, таких как расстояние между обнаружениями и распределением ковариации каждого обнаружения. Чтобы проиллюстрировать фундаментальное понятие, затраты присвоения для нескольких гипотез гипотетически даны в таблице [1].

Гипотезы присвоения	Сначала отсканируйте наблюдения (O _1x)	Второе наблюдение сканирования (O _2x)	Третье наблюдение сканирования (O _3x)	Стоимость
1	0	1	1	−10.2
2	1	2	0	−10.9
3	1	1	1	−18.0
4	1	1	2	−14.8
5	1	2	1	−17.0
6	2	0	1	−13.2
7	2	0	2	−10.6
8	2	2	0	−11.1
9	2	1	2	−14.1
10	2	2	2	−16.7

В таблице, 0 обозначает, что дорожка сопоставлена без обнаружения на том сканировании. Примите, что гипотезы, не показанные в таблице, являются усеченными путем пропускания или пропущенный из-за высокой стоимости. Чтобы кратко представлять каждую дорожку, используйте c _ijk, чтобы представлять стоимость для ассоциации наблюдения i на сканировании 1, j на сканировании 2, и k на сканировании 3. Например, для гипотезы 1 присвоения, c ₀₁₁ =-10.2. Несколько гипотез дорожки конфликтуют с другим в таблице. Например, два наиболее вероятных присвоения, c ₁₁₁ и c ₁₂₁ несовместимы, потому что они совместно используют то же наблюдение на сканированиях 1 и 3.

Цель решения задачи присвоения S-D состоит в том, чтобы найти наиболее вероятную совместимую гипотезу присвоения, составляющую все обнаружения. Когда S ≥ 3, однако, проблема, как известно, масштабируется с количеством дорожек и обнаружений на экспоненциальном (NP-трудном) уровне. Лагранжевый релаксационный метод обычно используется, чтобы получить оптимальное или субоптимальное решение для проблемы присвоения S-D эффективно.

Резюме вводит лагранжевому релаксационному методу для 3-D присвоения

Три сканирования данных имеют много M ₁, M ₂, и M ₃ наблюдения, соответственно. Обозначьте наблюдение за сканированием 1, 2, и 3 как i, j и k, соответственно. Например, i = 1, 2, …, M ₁. Используйте z _ijk, чтобы представлять гипотезу формирования дорожки O _1i, O _2j, и O _3k. Если гипотеза допустима, то z _ijk = 1; в противном случае, z _ijk = 0. Как упомянуто, c _ijk используется, чтобы представлять стоимость z ассоциация _ijk. c _ijk 0 для ложных предупреждений и отрицателен для возможных ассоциаций. Задача оптимизации S-D может быть сформулирована как:

$J (z) = \min_{i, j, k} \sum_{i = 0}^{M_{1}} \sum_{j = 0}^{M_{2}} \sum_{k = 0}^{M_{3}} c_{i j k} z_{i j k}$

подвергните трем ограничениям:

$\begin{array}{l} \sum_{i = 0}^{M_{1}} \sum_{j = 0}^{M_{2}} z_{i j k} = 1, \forall k = 1, 2, \dots, M_{3} \\ \sum_{i = 0}^{M_{1}} \sum_{k = 0}^{M_{3}} z_{i j k} = 1, \forall j = 1, 2, \dots, M_{2} \\ \sum_{j = 0}^{M_{2}} \sum_{k = 0}^{M_{3}} z_{i j k} = 1, \forall i = 1, 2, \dots, M_{1} \end{array}$

Функция оптимизации выбирает ассоциации, чтобы минимизировать общую стоимость. Эти три ограничения гарантируют, что каждое обнаружение составляется (или включенный в присвоение или обработанный как ложное предупреждение).

Лагранжевый релаксационный метод приближается к этой 3-D проблеме присвоения путем ослабления первого ограничения с помощью множителей Лагранжа. Задайте новый функциональный L (λ):

$L (λ) = \sum_{k = 0}^{M_{3}} λ_{k} [\sum_{i = 0}^{M_{1}} \sum_{j = 0}^{M_{2}} z_{i j k} - 1]$

где λ _k, k = 1, 2, …, M ₃ является множителями Лагранжа. Вычтите L из функции исходного объекта J (z), чтобы получить новую объектную функцию, и первое ограничение в k ослабляется. Поэтому 3-D проблема присвоения уменьшает до 2D задачи присвоения, которая может быть решена любым 2D методом присвоения. Для получения дополнительной информации см. [1].

Лагранжевый релаксационный метод позволяет первому ограничению быть мягко нарушенным, и поэтому может только гарантировать субоптимальное решение. Для большинства приложений, однако, это достаточно. Чтобы задать точность решения, метод использует разрыв решения, который задает различие между текущим решением и потенциально оптимистическим решением. Разрыв является неотрицательным, и меньший разрыв решения соответствует решению ближе оптимального решения.

Sensor Fusion and Tracking Toolbox обеспечивает assignsd решить для присвоения S-D с помощью лагранжевого релаксационного метода. Подобно K лучше всего 2D решатель присвоения assignkbest, тулбокс также предоставляет K лучший решатель присвоения S-D, assignkbestsd, который используется, чтобы предоставить несколько субоптимальных решений для проблемы присвоения S-D.

Смотрите, что Отслеживание Использует Распределенные Синхронные Пассивные Датчики для приложения присвоения S-D в статическом сплаве обнаружения.

Ссылки

[1] Блэкмен, S. и R. Пополи. Проект и анализ современных систем слежения. Радарная библиотека дома Artech, Бостон, 1999.

[2] Musicki, D. и Р. Эванс. "Объединенная Интегрированная Вероятностная Ассоциация Данных: JIPDA". Транзакции IEEE на Космических и Электронных системах. Издание 40, Номер 3, 2004, стр 1093 - 1099.

Документация