Эта тема обращается к программному обеспечению Simscape™ Multibody™ First Generation. Библиотека первого поколения будет скоро удержана от использования. Чтобы избежать проблем совместимости, создайте любые новые модели и преобразуйте любые существующие модели с помощью блоков второго поколения — доступные путем ввода команды smlib в командной строке MATLAB®.
Прежде, чем работать посредством этого исследования, консультируйтесь с предварительной системой управления, О Контроллерах и Объектах, и работайте посредством первого исследования системы управления, Анализируя Контроллеры. Это исследование основывается на результатах и концепциях последнего.
В дополнение к Simulink® и продукту Simscape Multibody, это использование исследования эти продукты:
Это второе тематическое исследование системы управления начинается путем показа вам, как создать и оптимизировать новый ПИД-регулятор. Это запускается с создания нового ПИД-регулятора с начала, определяет местоположение устойчивого состояния и линеаризует движение платформы об этом равновесии и настраивает линеаризовавшую динамику платформы, чтобы оптимизировать новый ПИД-регулятор. Исследование заканчивается путем представления многомерного синтеза как шага вне управления ПИДом, реализации более комплексного и реалистического многомерного контроллера и сравнения его производительности с новым ПИД-регулятором.
Этот раздел требует Control System Toolbox. Сохранение промежуточных версий модели и значений рабочей области рекомендуется.
Усиления ПИД-регулятора, установленные скриптом инициализации, предварительно оптимизированы. Предыдущее тематическое исследование, Анализируя Контроллеры, использует эти значения усиления в качестве примеров.
В остальной части этого исследования вы следуете более реалистическому сценарию, где усиления не первоначально известны, и вы используете инструменты системы управления в среде MATLAB, чтобы создать и оптимизировать отфильтрованный ПИД-регулятор.
Выскажите исходное предположение для интегратора (I), получают K i с размерным анализом. K у i есть сила/длина/время размерностей.
Исходное предположение для силы является одной шестой вес платформы и участков.
Исходное предположение для длины является областью значений вертикального движения в ссылочной траектории.
Исходное предположение для 1/время является собственной частотой, π/2π = 0,5 Гц.
Таким образом исходное предположение для усиления интегратора
Ki = 0.5*9.8*(top_mass/6+(upper_leg_mass+lower_leg_mass))/0.3 Ki = 7.1680e+003
Скрипт инициализации устанавливает переменную initCondI рабочей области к значению должен был поместить платформу в симметричное равновесие в начальном состоянии. С новым K i оцениваю, необходимо перекалибровать это начальное условие.
initCondI = ... (upper_leg_mass+lower_leg_mass+(top_mass*1.3/6))*9.81/Ki initCondI = 0.6839
Запустите, выключив ПИД-регулятор и прикладывая постоянную силу на платформу.
Щелкните правой кнопкой по подсистеме контроллера. Выберите Block Choice> Null Controller.
Щелкните правой кнопкой по Null Controller снова. Выберите Link Options> Go To Library Block.
Конфигурируемая библиотека подсистемы mech_stewart_controller открывается.
Под Edit выберите Unlock Library. Откройте Пустую шаблонную подсистему Контроллера.
В подсистеме, между Усилением и Силой (Выход) блоки, вставляют блок Integrator.
Откройте диалоговое окно Интегратора. Для Initial condition введите Ki*initCondI. Нажмите OK.
Закройте Пустой Контроллер. Сохраните и закройте mech_stewart_controller библиотеку.
Назад в mech_stewart_control, обновите схему (Ctrl+D).
В командной строке введите Ki*initCondI.
Это - ваше первое предположение для силы контроллера на одном участке: продукт вашего интегратора ПИДа (I) получает предположение и ваше предположение начального состояния контроллера.
Теперь наблюдайте эффект этой постоянной силы на платформе.
В подсистеме Траектории Ссылки Участка, набор положение Переключателя Траектории к вниз.
Откройте Осциллограф и запустите симуляцию. Сила управления меньше веса платформы. Платформа ускоряется вниз.
Этот раздел требует Control System Toolbox и Simulink Control Design . Сохранение промежуточных версий модели и значений рабочей области рекомендуется.
Критический шаг в системе управления должен изучить ответ объекта, которым управляют к маленьким воздействиям в его движении [5]. Этот шаг требует
Обрезка платформы или нахождение рабочей точки. Это - траектория времени, удовлетворяющая определенным предшествующим условиям, которые вы задаете.
Здесь вы ищете простую, полезную рабочую точку симметричного равновесия, куда платформа не перемещается.
Линеаризация движения платформы о рабочей точке.
Вы сохраняете результаты линеаризации использовать в следующем разделе, Улучшая Новый ПИД-регулятор.
Как описано в Обрезке и Линеаризации Через Обратную Динамику, можно обрезать модели Simscape Multibody во многих отношениях. Control System Toolbox™ и Simulink Control Design™ обеспечивают линейные аналитические инструменты, более богатые и более мощные, чем, какое одно только программное обеспечение Simulink и Simscape Multibody предлагают.
Теперь настройте модель для обрезки. В режиме Trimming механические состояния модели являются 40 ограничениями, которые уменьшают свободные 52 (прямая динамика) утверждает в эти 12 независимых государств.
Убедитесь, что модель наблюдает эти настройки.
Сохраните подсистему контроллера набором Block Choice к Null Controller и производным типом к Filtered Derivative.
Подавите Переключатель Траектории (статическая траектория) в подсистеме Траектории Ссылки Участка.
Сбросьте аналитический режим Simscape Multibody к обрезке.
Откройте подсистему Объекта. Дважды кликните оранжевый блок Machine Environment. Найдите вкладку Parameters.
Для Analysis mode, изменение выпадающее меню к Trimming. Нажмите OK и закройте подсистему.
Наблюдайте обрезку выходные блоки, которые появились в верхнем левом углу основной модели.
![]()
Затем найдите рабочую точку для объекта платформы Стюарта.
Выберите точки линеаризации в своей модели можно следующим образом. Щелкните правой кнопкой, в свою очередь, на каждой из линий Сигнала Simulink, задающих ввод и вывод подсистемы Объекта:
Силы участка (вводятся)
Pos (выход)
В контекстном меню каждой сигнальной линии, под Linearization Points, выбором
И Input Point и Open Loop для входной линии
И Output Point и Open Loop для выходной линии
Выбор свойства разомкнутого цикла для этих сигналов повреждает обратную связь от диспетчера к объекту назад контроллеру. Объект вместо этого берет данный набор внешне наложенных сил контроллера.
Затем из панели меню модели выберите Analysis> Control Design> Linear Analysis. Окно Control and Estimation Tools Manager открывается.
Слева от окна менеджера выберите узел Operating Points. Затем направо, выберите вкладку Compute Operating Points. Нажмите кнопку Sync with Model в нижней части вкладки.
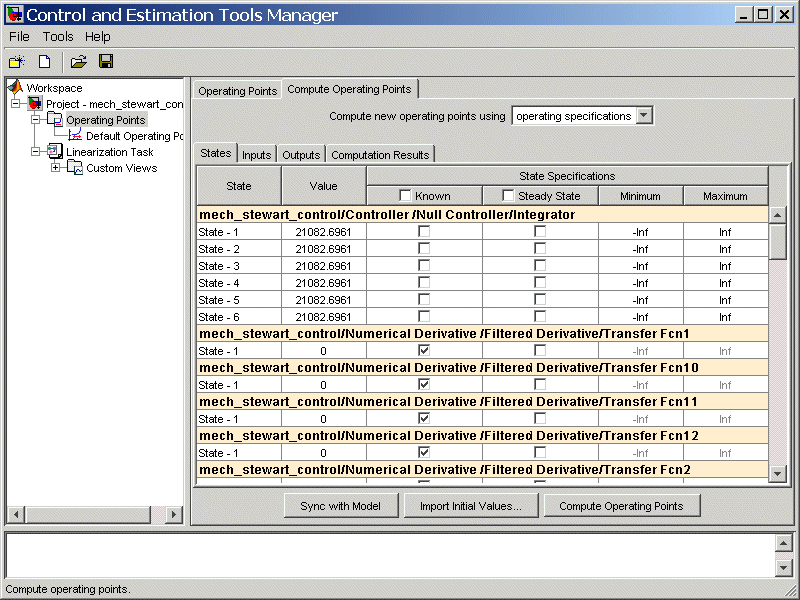
Подвкладкой по умолчанию является States. Флажки Steady State устанавливаются по умолчанию. Этот выбор ищет рабочую точку объекта, где платформа в покое относительно ее начальной настройки.
Исследуйте состояния путем прокручивания вниз в окне States.
Существует шесть состояний, сопоставленных с пустым блоком диспетчера Интегрэтора.
Снимите флажки Steady State для этих состояний. Обрезка не будет содержать сигнал контроллера, как зафиксировано.
Ниже этих шести двенадцать состояний, сопоставленных с Передачей блоки Fcn в Фильтрованной Производной подсистеме.
Освободите их от того, чтобы быть зафиксированным путем снимания их флажков Steady State. Сделайте их значения (0) известными путем устанавливания их флажков Known.
Остальная часть состояний сопоставлена с положениями и скоростями соединений участка платформы Стюарта. Только шесть из этих состояний независимы. Другие ограничиваются. Оставьте их настройки как значения по умолчанию.
Переместитесь в подвкладку Outputs. Под Output Specifications установите флажок Known (самый верхний флажок в том столбце). Это действие задает все выходные параметры, отклонения состояния от желаемой рабочей точки. Существует 40 состояний (ограничения) в режиме Trimming.
Выходные значения заданы в столбце Value. Значения являются всем нулем, указывая, что всем ограничениям на состояния (спецификации рабочей точки) нужно удовлетворить в допуске.
От панели меню окна менеджера выберите Tools> Options. Окно Options открывается. Выберите вкладку Operating Point Search.
В области Optimization Method выберите Nonlinear least squares в меню Optimization Method.
Оставьте другие значения по умолчанию. Нажмите OK. Завершения окна Options.
Назад в Control and Estimation Tools Manager, нажмите кнопку Compute Operating Points в нижней части вкладки Compute Operating Points.
Подвкладка Computation Results указывает на прогресс обрезки. По окончании это должно указать, что спецификациям рабочей точки успешно соответствовали.
В узле Operating Points налево, новый подузел Operating Point появляется, Operating Point, содержа результаты этой обрезки.
Исследуйте и сохраните результаты рабочей точки.
Нажмите Operating Point. Посмотрите на States и вкладки Outputs.
Под Outputs, значения Desired dx (если не отмеченный N/A) нуль. Для механических состояний (ограничения) значения Actual dx (отклонения от требуемой рабочей точки) являются нулем в допуске.
Это не верно для состояний Контроллера, которых вы не потребовали, чтобы исчезнуть. Фильтрованные Производные состояния являются всем нулем.
Сохраните эту рабочую точку путем щелчка правой кнопкой по Operating Point и выбор Export. За исключением имени, оставьте значения по умолчанию.
Для Variable Name введите oppoint_PLANT. Нажмите OK.
У вас теперь есть объект рабочей области (opcond.OperatingPoint класс) названный oppoint_PLANT представление объекта, содержащего все еще в начале симуляции (t=0). Сохраните этот объект для дальнейшего использования.
Исследуйте его состояния путем ввода
oppoint_PLANT % List plant states at t=0
Сбросьте условие начальной буквы контроллера к новой рабочей точке.
initCondI = oppoint_PLANT.States(1).x(1);
Переключатель Now модель назад к режиму Forward Dynamics. Механические состояния являются теперь 52 древовидными состояниями, соответствующими неразрезанным объединенным примитивам.
Откройте подсистему Объекта, затем ее оранжевый блок Machine Environment. Найдите вкладку Parameters.
В выпадающем меню Analysis mode выберите Forward Dynamics. Нажмите OK и закройте подсистему.
Затем линеаризуйте движение объекта о рабочей точке, в которой вы задали ранее. Возвратитесь к менеджеру по Инструментам Управления и Оценки.
Выберите Tools> Options. В диалоговом окне Options выберите вкладку Linearization State Ordering.
Нажмите кнопку Sync with Model в нижней части, затем нажмите OK.
Теперь выберите узел Linearization Task к левому, затем вкладка Operating Points. Выберите Operating Point под названием Operating Point.
В нижней части вкладки убедитесь, что флажок Plot linear analysis result in a устанавливается. Затем выберите тип графика в выпадающем меню. Например, выберите Bode response plot.
Затем нажмите кнопку Linearize Model. Linear System Analyzer открывается большой семьей, Предвещают графики отклика.
Для дальнейшего использования можно выбрать другие типы графика отклика путем щелчка правой кнопкой по одному из графиков и, под Plot Type, выбора различного графика, таких как Bode, Step или Impulse. (Вы не должны возвращаться к Linearization и повторно линеаризовать модель.)
Эта линеаризация объекта запускается с шести входных параметров (силы участка) и 12 выходных параметров (шесть положений участка и шесть скоростей участка). Linear System Analyzer отображает 6 x 12 = 72 графика отклика. Просмотреть один график индивидуально,
Щелкните правой кнопкой по любому из 72 графиков и выберите I/O Selector. Диалоговое окно I/O Selector открывается.
Это диалоговое окно позволяет вам, чтобы выбрать любой ответ одного выхода относительно одного входа. Чтобы видеть что график в Linear System Analyzer, кликните по соответствующей черной точке.
Каждый график показывает, как одни из выходных параметров (положение или скорость) отвечают на приложение маленькой силы в одном из входных каналов. Различные типы графика (импульс, шаг, Предвещают, и т.д.) дают к различным аспектам ответа.
Экспортируйте результаты своей линеаризации.
Выберите File> Export в Linear System Analyzer.
Выберите свою модель и дайте ей уникальное имя (вызовите ее sys) под Export As.
Нажмите Export to Workspace. Модель сохранена как объект LTI. Переменным классом является ss, каноническая форма пространства состояний используется Simulink.
Сохраните этот объект LTI для следующего раздела, где вы используете его, чтобы улучшить ПИД-регулятор.
Можно применить эти результаты к другим контроллерам (см. Синтезирование Устойчивого, Многоканального Контроллера), а также выберите другие рабочие точки.
Этот раздел требует Control System Toolbox и Simulink Control Design . Сохранение промежуточных версий модели и значений рабочей области рекомендуется.
Чтобы возобновить этот раздел, необходимо завершить предыдущий раздел, Обрезав и Линеаризуя Движение Платформы.
В этом разделе вы используете результаты линеаризации создать контроллер, чтобы лучше совпадать с объектом. Эта информация позволяет вам преобразовывать информацию о разомкнутом цикле о контроллере и объекте в поведение с обратной связью двойной системы.
ПИД-регулятор действует как тот же контроллер на каждом из участков платформы. Можно улучшить ответ диспетчера на движение каждого участка путем работы с диагональными компонентами ответа объекта. Эти компоненты представляют ответ движения участка на силу, действующую на тот участок. Эта парадигма системы управления является одной - в, одной (SISO). Симметрией разработка настроек PID с одним из поведения управления участка оптимизирует их для других пяти.
Подход SISO игнорирует связь между участками. Последний раздел этого исследования, Синтезируя Устойчивый, Многоканальный Контроллер, занимается многоканальной связью, чтобы достигнуть более точного проектирования контроллера.
От предыдущего раздела, Обрезая и Линеаризуя Движение Платформы, у вас должны быть они сохраненные в вашей рабочей области:
Линеаризовавшая модель объекта управления как объект LTI (ss класс) названный sys
Условие начальной буквы контроллера initCondI сбросьте к рабочей точке
Полезные промежуточные версии модели и MAT-файлы переменной рабочей области
В этом разделе сохраните производный блок как Filtered Derivative и ПИД-регулятор как biproper.
Многие из механического устройства утверждают в sys ограничиваются. Удалите их с sminreal команда. Это сокращение работает со структурой sys, вместо (как minreal) с числовыми свойствами sys.
G = sminreal(sys); % Structural reduction of linearized sys
G теперь представляет уменьшаемый линеаризовавший объект.
Один способ получить ощущение эффекта управления с обратной связью ПИДа на движении платформы Стюарта состоит в том, чтобы систематически изменять усиления, сокращение частоты и насыщение силы, в то время как фиксирующий ссылочная траектория и начальные условия платформы.
Чем больший K d относительно K p и K i, тем более чувствителен контроллер к мгновенным изменениям в ссылочном сигнале. (То же самое верно для K p относительно K i.) Производный термин подчеркивает быстрое изменение. С другой стороны, если K d мал, контроллер более вял в ответ. K, который i называю, подчеркивает память об ошибках движения мимо. Основной компромисс системы управления
Более быстро реагирующий ПИД-регулятор также менее устойчив против высокочастотного (короткий масштаб времени) воздействия, такие как шум.
Более устойчивый контроллер является менее быстро реагирующим к обратной связи.
Для большого фильтрующего постоянного A biproper передаточная функция c(s) ведет себя в маленьком s почти точно как неподходящий C(s). Но когда вы уменьшаете A, c(s) ведет себя меньше как C(s). Во временном интервале, для меньшего A, контроллер c(s) показывает больше переходного отклонения от чистого производного поведения C(s).
ПИД-регулятор также зависит от предела насыщения силы, установленного в рабочей области force_act_max. То, чтобы заставлять насыщение силы ограничить слишком маленький означает, что контроллер не может привести в движение участки достаточно, чтобы заставить их не отставать от ссылочного сигнала траектории. Движение платформы перемещается к нестабильности с более низким пределом насыщения силы. Слишком низкий предел в конечном счете дает к движению, которое является неприемлемо экстремальным значением или абсолютно нестабильный. В какой-то степени можно компенсировать более низкий предел насыщения силы путем создания контроллера более быстро реагирующим.
Лучший способ оптимизировать ПИД-регулятор состоит в том, чтобы анализировать открытое - и ответ машины с обратной связью с Design Tool SISO.
Откройте SISO Design Tool путем ввода
controlSystemDesigner(G(1,1)); % SISO design tool for first leg-leg pair
Design Tool открывается контроллером единицы (компенсатор), C(s) = 1. Используйте меню Help для получения дополнительной информации о Design Tool, включая то, как интерпретировать символы графика.
Root Locus Editor налево показывает ответ CG/(1+CG) с обратной связью, s - плоские полюса, нули и корневые годографы. Open-Loop Bode Editor направо показывает разомкнутому циклу ответ объекта CG, включая полюса и нули.
Ответ с обратной связью имеет восемь полюсов, четыре на лево-половине и четыре на правильной половине s - плоскость, последняя нестабильность указания. Диаграмма Боде разомкнутого цикла отображает запасы по амплитуде и фазе.
Design Tool SISO с объектом платформы Стюарта в покое и контроллером единицы
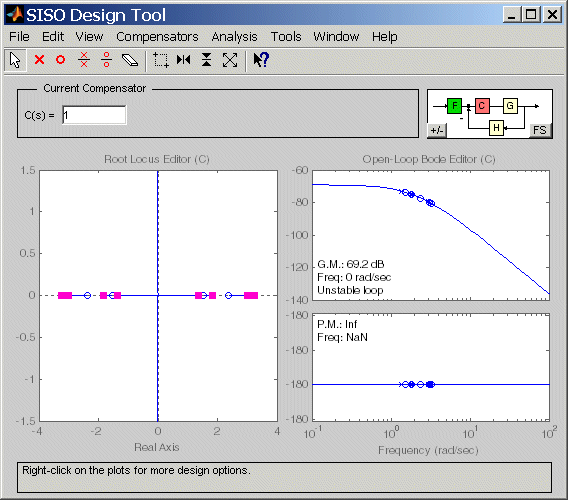
Чтобы спроектировать biproper ПИД-регулятор, добавьте два нуля и два полюса и настройте полное усиление. Наблюдайте эти общие правила для полюсов и нулей:
Коэффициенты числителя, включая полное усиление, должны быть положительными. Самый легкий способ гарантировать это для обоих нулей, чтобы иметь отрицательные действительные части.
Один полюс должен произойти в нуле. Это соответствует интегратору (I) часть.
Другой полюс должен иметь отрицательную действительную часть.
Реализовывать,
Выберите Compensators> Edit> C. Диалоговое окно Edit Compensator C открывается. Добавьте полюса и нули. Нажмите OK. Диалоговые завершения.
В графике корневого годографа можно переместить контроллер и полюса с обратной связью и нули вокруг путем перетаскивания их с мышью. Когда вы перемещаете полюса с обратной связью, вы также изменяете полное усиление контроллера. Обязательно оставьте первоначально устойчивые полюса с обратной связью в левой полуплоскости.
В Предвещать редакторе можно переместиться, разомкнутый цикл (контроллер) подпирает шестами и обнуляет путем перетаскивания их. Можно также изменить запасы по амплитуде и фазе.
Контроллер Design Tool SISO форма является κ (1 +αs) (1 +βs)/s (1 +γ] s). Полным κ усиления управления является K i в этой форме.
Для K i, используйте значение своего первого предположения, найденного ранее в Разработке Нового ПИД-регулятора.
Чтобы оптимизировать ваш контроллер, измените его ответ, чтобы подавить нежелательного и улучшить желательную обратную связь. Цели, типичные в проблемах управления, являются ответом высокого усиления в низких частотах, чтобы достигнуть производительности отслеживания и уменьшающегося ответа в высоких частотах, чтобы ограничить чувствительность диспетчера к изменениям объекта и шуму.
Движения платформы имеют низкую пропускную способность, обычно только некоторые Герц (Гц). Система должна иметь сильную реакцию некоторые Гц (ω = приблизительно 10 рад/с), затем падающий ответ для более высоких частот.
Один полюс контроллера должен всегда оставаться в нуле. Пять системных полюсов имеют положительные (нестабильные) действительные части, результат первого матча, связывающегося с другими пятью. Вы не можете устранить их в анализе SISO.
Улучшите контроллер
Создание ненулевого контроллера орудовать шестами более отрицательный. Это увеличивает A и увеличивает запас по фазе при уменьшении запаса по амплитуде.
Улучшение переходного процесса путем корректировки нулей контроллера.
Понижение запаса по амплитуде путем повышения полного Предвещает ответ. Это увеличивает полное усиление контроллера κ = K i.
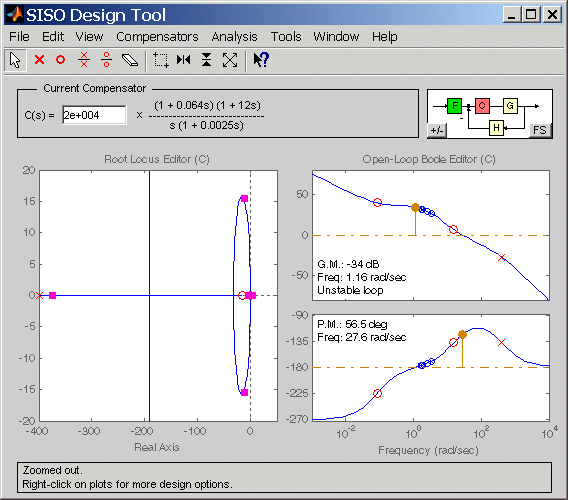
Если у вас есть удовлетворительный контроллер, можно экспортировать новый оптимизированный biproper закон о надзоре в рабочую область и анализировать его там, чтобы переопределить отфильтрованные параметры ПИД-регулятора K i, K p, K d и A.
Экспортируйте модифицированный компенсатор от Design Tool SISO.
Перейдите к File> Export. Выберите Compensator. Переименуйте его cBiproperOpt под Export as.
Затем нажмите Export to Workspace.
cBiproperOpt форма нулей, полюсов и усиления (объект LTI класса zpk). Например,
cBiproperOpt
Zero/pole/gain:
6171074.4994 (s+15.51) (s+0.08378)
----------------------------------
s (s+400)Извлеките biproper параметры ПИД-регулятора путем инвертирования нулей s ±, полюса, и получите K. Стандартная форма нулей, полюсов и усиления
c(s) = K(s - s +)(s - s-)/s(s+A) = [(K p + AK d)*s2 + (Ki + AKp)*s + AKi] /s(s + A)
A = отрицание biproper ненулевого полюса
Усиления:
K i = Ks +s-, K p = - [K (s + + s-) + K i]/A, K d = (K - K p)/A
Сбросьте свои переменные рабочей области соответственно.
[z,p,k] = zpkdata(cBiproperOpt) % Extract ZPK data from cBiproper
A = -p{1,1}(2) % Extract nonzero pole
Ki = k*z{1,1}(1)*z{1,1}(2)/A % Extract Ki gain
Kp = -(k*(z{1,1}(1) + z{1,1}(2)) + Ki)/A % Extract Kp gain
Kd = (k - Kp)/A % Extract Kd gainПроверяйте, что симметричное равновесие устойчиво с вашим новым контроллером.
Убедитесь, что Переключатель Траектории установлен во вниз.
Обновите схему (Ctrl+D) и повторно выполните модель.
Точка для обрезки редко точна. Обычно существует небольшая, но ненулевая ошибка движения, когда платформа ослабляется к равновесию.
Теперь протестируйте движение платформы с движущейся траекторией, и ваше новое повторно настроило biproper закон о надзоре.
Задержите Переключатель Траектории к.
Перезапустите модель. Необходимо видеть разумные ошибки движения и силы участка, кроме, возможно, для начального переходного процесса.
Зафиксируйте Ошибки Движения от регистрируемой структуры сигналов sigsOut.
pid_opt_TS = sigsOut.('Motion Errors'); % Record motion errorsЭта часть исследования требует Control System Toolbox и Robust Control Toolbox.
Чтобы завершить этот раздел, необходимо завершить предыдущий раздел, Улучшив Новый ПИД-регулятор.
Контроллеры, которые вы спроектировали до сих пор в этом и предыдущих исследованиях системы управления, основаны на классических методах ПИДа, где каждый канал подвергается тому же закону о надзоре, и закон о надзоре настраивается один канал за один раз. Этот подход пропускает перекрестную связь, влияние, которое сила на одном участке платформы оказывает на движение других участков.
В этом разделе вы перепроектируете контроллер платформы Стюарта при помощи современных методов, которые принимают во внимание многоканальную связь и реализацию устойчивого контроллера H-бесконечности [6], [7].
От предыдущих разделов у вас должны быть они сохраненные в вашей рабочей области:
Уменьшаемое представление пространства состояний G из объекта
Структура временных рядов pid_opt_TS
Перед запуском,
Из его контекстного меню, под Block choice, переключают подсистему контроллера на H_inf Controller.
Убедитесь, что производная подсистема остается установленной в Filtered Derivative, и Переключатель Траектории в подсистеме Траектории Ссылки Участка установлен в.
Исследуйте подсистему контроллера, которая реализована через пространство состояний.
Подсистема контроллера H-бесконечности платформы Стюарта
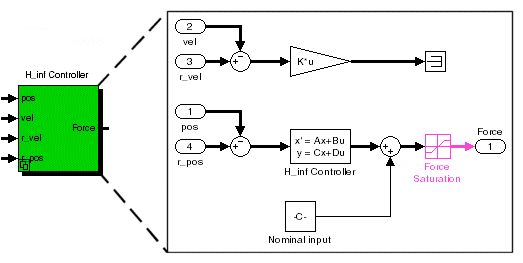
Запустите путем определения желаемого ответа разомкнутого цикла |C*G(1,1)| и постройте его сингулярные значения. Например,
Lsd = zpk([],[-1000 0],612770) % Define desired loop shape Zero/pole/gain: 612770 ---------- s (s+1000) sigma(Lsd) % Plot singular values
Просмотрите ответ с обратной связью, сгенерированный этой формой цикла путем ввода:
step(feedback(Lsd,1)) % Feedback step response
Желаемая форма цикла: Сингулярные значения
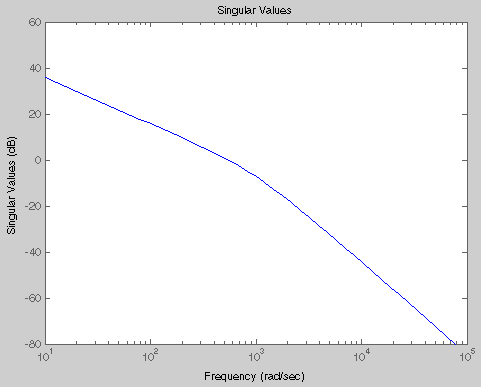
Теперь создайте контроллер, использующий желаемую форму цикла и ответ объекта:
[K_ls,CL,GAM,INFO] = loopsyn(G,Lsd); % Synthesize controller
Проверяйте размер контроллера путем ввода
size(K_ls) % Check size of loopsyn controller
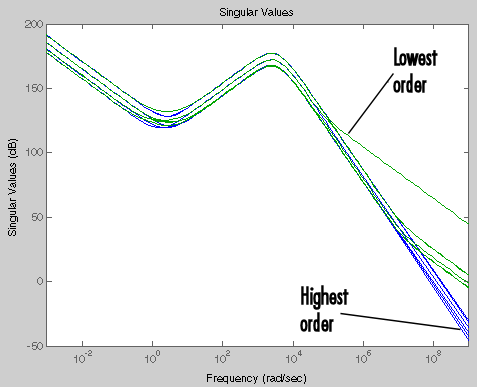
У контроллера в качестве примера есть 48 состояний. Это обычно невозможно реализовать контроллер такой высокого уровня и вычислительной интенсивности. Так попытайтесь уменьшать контроллер до 24-го порядка:
Kr_ls = reduce(K_ls,24); % Reduce controller order
Чтобы оценить, сколько состояний можно проигнорировать (обрезают), строят обоих полные и уменьшаемые сингулярные значения
sigma(K_ls,Kr_ls) % Plot singular values
Полные и уменьшаемые синтезируемые циклом контроллеры: Сингулярные значения
От синтезируемой формы цикла матрицы извлечение, должен был задать модель в пространстве состояний, используемую в Подсистеме контроллера H_inf.
[Ak,Bk,Ck,Dk] = ssdata(Kr_ls); % Extract state space model
Запустите синтезируемые циклом модели контроллеров. Затем зафиксируйте ошибки движения.
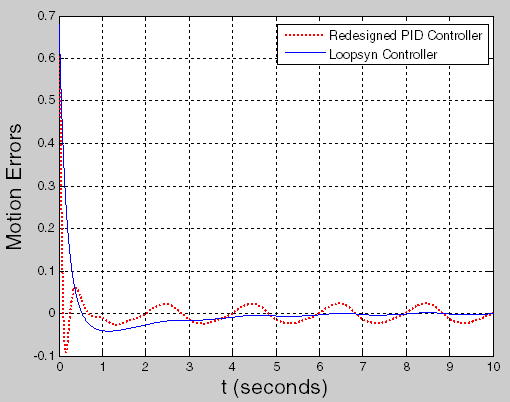
loopsyn_TS = sigsOut.('Motion Errors'); % Record motion errorsНаконец, сравните ошибочные данные о движении от этих двух диспетчеров:
Перепроектированный ПИД
Устойчивый синтезируемый циклом
В командной строке, введите:
figure
plot(pid_opt_TS.Time,pid_opt_TS.Data(1,:),'r', ...
loopsyn_TS.Time,loopsyn_TS.Data(1,:),'b')
ylabel('Motion Errors','FontSize',16)
xlabel('t (seconds)','FontSize',16)
legend('Redesigned PID Controller','Loopsyn Controller')Кроме начального переходного процесса, синтезируемый циклом контроллер выполняет лучше, чем перепроектированный ПИД-регулятор. В этом примере последние разовые устойчивые ошибки движения контроллера являются больше, чем меньший порядок величины и не показывают колебательного “вызова”.
Перепроектированный ПИД и синтезируемые циклом ошибки движения системы управления