Линеаризация механических моделей

Предупреждение

Это содержимое характерно для программного обеспечения Simscape™ Multibody™ First Generation. Функции первого поколения намечают, чтобы быть удержанными от использования и нужно избежать.

О линеаризации и программном обеспечении Simscape Multibody

Simulink® linmod команда создает модели в пространстве состояний линейного независимого от времени (LTI) из моделей Simulink. Это линеаризует каждый блок отдельно. Можно использовать эту команду, чтобы сгенерировать модель в пространстве состояний LTI из модели Simscape Multibody, например, служить входом к командам Control System Toolbox, которые генерируют модели контроллеров. linmod команда позволяет вам задавать точку в пространстве состояний, о котором это линеаризует модель (рабочая точка). Необходимо выбрать точку, где модель находится в равновесии, т.е. где сетевая сила на модели является нулем. Можно использовать trim Simulink команда, чтобы найти подходящую рабочую точку (см. Обрезающие Механические Модели). По умолчанию, linmod использует адаптивный метод возмущения, чтобы линеаризовать модель. Диалоговое окно Среды Машины позволяет вам требовать того linmod используйте фиксированный метод возмущения вместо этого (см. Выбор Analysis Mode). Примеры затем следующее иллюстрируют использование linmod линеаризовать модели Simscape Multibody.

Консультируйтесь с документацией Simulink для больше на линеаризации моделей (Simulink). Можно также ввести help linmod в командной строке MATLAB®.

Ограничения на линеаризацию механических моделей

Существуют ограничения на то, как вы линеаризуете механические модели.

  • Если вы задаете какие-либо объединенные примитивные начальные условия с блоками Joint Initial Condition Actuator, эти начальные значения условия всегда заменяют любые начальные значения вектора состояния, заданные через linmod команда.

    Объединенные примитивы с блоками JICA предпочтительно выбраны для набора независимых государств в линеаризации.

  • Постарайтесь не включать дискретные события или разрывы движения в линеаризовавшей модели. Если вы включаете событие - или инициировавшие разрыв блоки, гарантируете, что машина не вызывает разрывы, когда это перемещается через линеаризовавший режим, вы моделируете.

    Использование блоков Joint Stiction Actuator в линеаризовавшей модели вызывает ошибку.

  • Поскольку замкнутые циклы налагают ограничения на состояния, вы не можете линеаризовать модель Simscape Multibody с обратной связью с linmod2 команда.

Линеаризация в присутствии приведения в действие движения

Линеаризация Simscape Multibody использует только ускорение в качестве независимого входа приведения в действие движения, потому что это эквивалентно силе или крутящему моменту. Подобное ограничение содержит для обрезки модели; смотрите Обрезку в присутствии Приведения в действие Движения. Как следствие единственный сигнал приведения в действие движения, который может быть установлен как вход модели, является ускоряющим сигналом.

Если вы хотите линеаризовать модель Simscape Multibody, содержащую приводы движения, вы должны

  1. Заставьте части скорости и положения/угла приведения в действие движения сигнализировать о зависимом только на ускоряющем сигнале

  2. Сделайте скорость и положение/угол сопоставимыми с ускоряющей частью при помощи блоков Integrator. Сигнал приведения в действие движения является вектором с компонентами, упорядоченными как положение/угол, скорость и ускорение, соответственно.

    Этот метод рекомендуется в Стабилизации Числовых Производных в Сигналах Приведения в действие. Это требуется здесь.

Линеаризация Simscape Multibody использует только ускорение в качестве независимого входа приведения в действие движения, потому что это эквивалентно силе или крутящему моменту. Как следствие только ускоряющий сигнал может использоваться в качестве независимого входа приведения в действие движения.

Подобное ограничение содержит для обрезки модели; смотрите Обрезку в присутствии Приведения в действие Движения.

Приведение в действие движения как вход модели для линеаризации

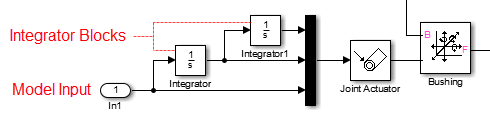
Линеаризация в присутствии Приведения в действие Движения.  Можно поместить входной порт модели в другую часть модели, затем питать тот вход как ускорение в привод движения с линией Сигнала Simulink. Необходимо все еще вывести сигналы приведения в действие движения скорости и положения/угла таким же образом: путем интеграции любого сигнала вы используете в ускорении однажды и дважды, соответственно.

Линеаризация открытой топологии: двойной маятник

Рассмотрите двойной маятник, первоначально зависающий прямо вверх и вниз.

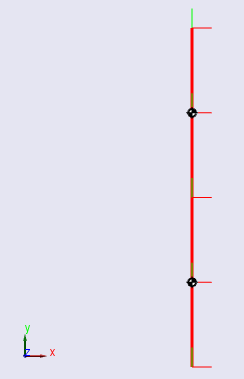
Сетевая сила на маятнике является нулем в этой настройке. Маятник находится таким образом в равновесии.

Откройте mech_dpend_forw модель.

Линеаризация модели

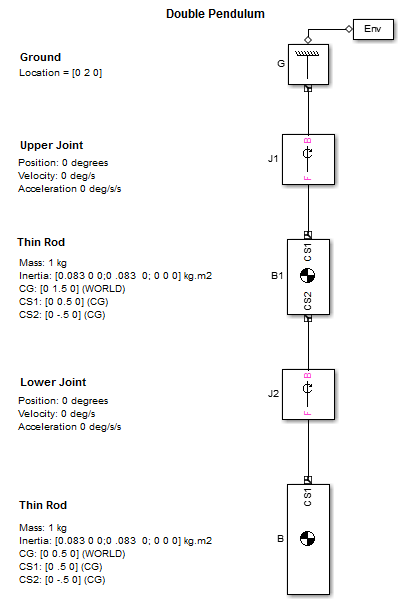
Чтобы линеаризовать эту модель, войти

[A B C D] = linmod('mech_dpend_forw');

в командной строке MATLAB. Эта форма linmod команда линеаризует модель о начальном состоянии модели.

Примечание

Объединенные начальные условия, заданные с блоками IC всегда, заменяют любые начальные значения вектора состояния, переданные linmod команда.

Двойная модель маятника в этом примере не содержит блоков IC. Начальные условия заданы с linmod команда поэтому реализована без модификации.

Получение линеаризовавшей модели в пространстве состояний

Матрицы A, B, C, D, возвращенный linmod команда соответствует стандартному математическому представлению модели в пространстве состояний LTI:

где x является вектором состояния модели, y являются свои выходные параметры, и u является своими входными параметрами. Двойная модель маятника не имеет никаких вводов или выводов. Следовательно, только A не является пустым. Это уменьшает модель в пространстве состояний для двойного маятника к

где

A =
         0         0    1.0000         0
         0         0         0    1.0000  
 -137.3400   39.2400         0         0
   39.2400  -19.6200         0         0

Эта модель задает отношение между производными состояния и состояниями двойного маятника. Вектор состояния модели LTI имеет тот же формат как вектор состояния модели Simscape Multibody. Simscape Multibody mech_stateVectorMgr команда дает формат вектора состояния можно следующим образом:

StateManager = mech_stateVectorMgr('mech_dpend_forw/G');
StateManager.StateNames

ans =
    'mech_dpend_forw/J2:R1:Position'
    'mech_dpend_forw/J1:R1:Position'
    'mech_dpend_forw/J2:R1:Velocity'
    'mech_dpend_forw/J1:R1:Velocity'

Умножающий право A вектором состояния x дает к дифференциальным уравнениям состояния, соответствующим модели LTI двойного маятника,

где

Массив коэффициентов на правой стороне дифференциальных уравнений представляет матрицу частот в квадрате. Собственные значения этой матрицы являются отрицательными частотами в квадрате режимов ответа системы. Эти режимы характеризуют, как двойной маятник отвечает на небольшие возмущения около рабочей точки, которая вот равновесие без силы.

Следующая модель Simulink реализует модель в пространстве состояний, представленную этими уравнениями.

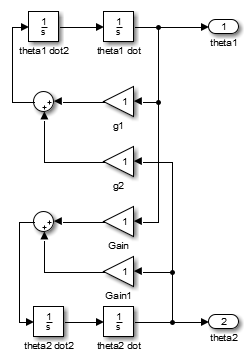
Моделирование ошибки линеаризации

Эта модель в свою очередь позволяет создание модели, расположенной в mech_dpend_lin это вычисляет ошибку приближения LTI.

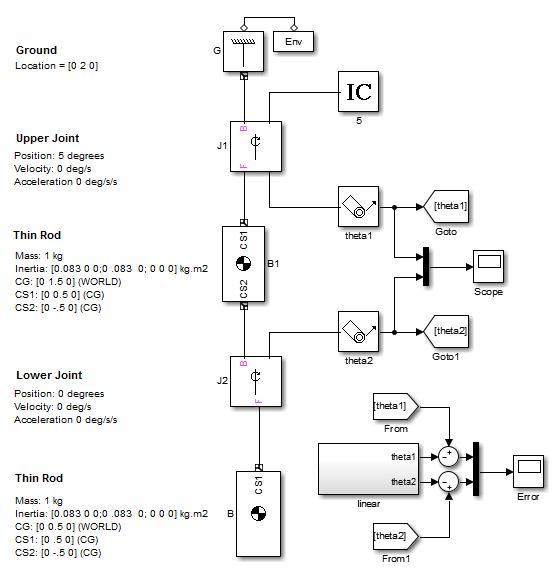
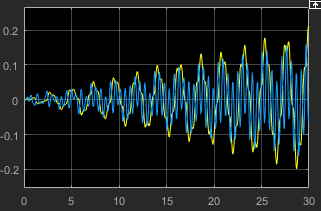
Выполнение модели дважды с верхним соединением отклонило 2 градуса и 5 градусов, соответственно, показывает увеличение по ошибке, когда начальное состояние системы отклоняется от положения равновесия маятника и когда время протекает. Это - ожидаемое поведение линейного приближения пространства состояний.

Ошибка в начальном отклонении на 5 градусов

Линеаризация с обратной связью: машина четырёхзвенника

Функция Control System Toolbox

Этот раздел требует доступа к minreal функция Control System Toolbox.

Линеаризация машины с обратной связью является более комплексной, чем анализ открытой топологии. Каждый замкнутый цикл в машине налагает неявные ограничения, которые представляют некоторые степени свободы (число степеней свободы) зависимый. Линеаризация такой системы должна распознать, что не все число степеней свободы независимо. Прямая реализация linmod команда приводит к избыточным системным состояниям. Можно устранить их с minreal функция, которая находит минимальное пространство состояний, должна была представлять вашу линеаризовавшую модель. Гарантировать тот minreal производит непустое пространство состояний, необходимо линеаризовать машину с обратной связью по крайней мере с одним входом u и одним выходом y.

mech_four_bar_lin иллюстрирует это сокращение независимого числа степеней свободы: из этих четырех шарнирных соединений только один - независимая степень свободы, которая может быть взята в качестве любого из revolutes. Эта модель задает переменные рабочей области для того, чтобы сконфигурировать начальную геометрию длин и углов (выраженный в модели в метрах и радианах, соответственно). Запустите модель в режиме Forward Dynamics.

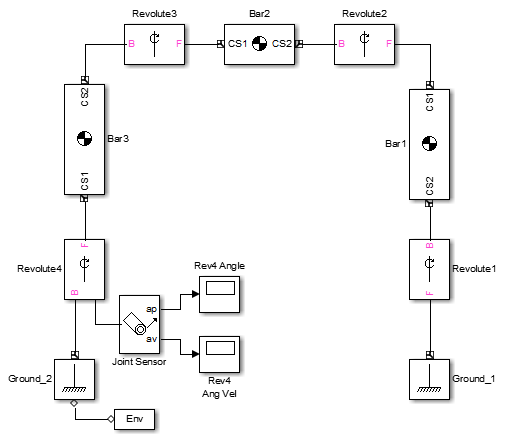
Рассмотрите стратегию линеаризовать модель об (устойчивом) естественном равновесии четырёхзвенника. Вы сначала находите естественную настройку равновесия, которая лучше всего выполняется путем анализа ограничений цикла, высказывания предположения, и затем использования trim команда, чтобы определить равновесие точно. После выбора системного ввода и вывода вы затем линеаризуете систему.

Анализ геометрии четырёхзвенника и ограничения с обратной связью

Можно определить ограничения, и независимое число степеней свободы четырёхзвенника с геометрическими и тригонометрическими тождествами применилось к его четырехсторонней форме. Длинами панелей является l 1, l 2, и l 3, с фиксированной основой, имеющей длину l 4.

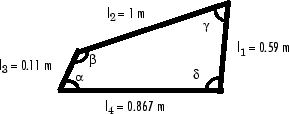
Эти четыре угла поворота шарнира удовлетворяют α + β + γ + δ = 2π. Предположите сокращать четырехугольник по диагонали от α до γ вершин, затем от β до δ вершин. Закон косинусов применился к этим диагоналям и треугольникам так сформированные результаты в двух ограничениях:

l 12 + l 22 - 2l1l2cosγ = l 32 + l 42 - 2l3l4cosα

l 22 + l 32 - 2l2l3cosβ = l 12 + l 42 - 2l1l4cosδ

Эти четыре угла таким образом подвергаются трем ограничениям. Выберите α (угол заводной рукоятки) как независимая степень свободы. Можно определить β, γ, и δ от α путем инвертирования ограничений.

Высказывание предположения равновесия

Сначала угадайте естественное равновесие. Очевидное предположение для естественного равновесия для заводной рукоятки (Панель 3), чтобы указать прямо вниз, α =-90o.

  1. Используйте четырехсторонние ограничения, чтобы найти

    β = 313.2o, γ = 60.3o, и δ = 76.5o

  2. Переопределите углы рабочей области к этим значениям (преобразованный в радианы).

    alpha = -90*pi/180; beta = 313.2*pi/180; gamma = 60.3*pi/180; 
delta = 76.5*pi/180;
beta2 = pi - gamma - delta; delta2 = pi - delta;

  3. Обновите схему и запустите модель снова. Эта настройка не является естественным равновесием, но это близко.

Определение естественного равновесия с trim

Теперь найдите естественное равновесие точно путем обрезки четырёхзвенника способом, похожим на Ограниченную Обрезку Машины Четырёхзвенника, но без внешнего приведения в действие крутящего момента. Revolute1 уже вручную сконфигурирован, чтобы быть соединением сокращения в замкнутом цикле, гарантируя, что степень свободы, представленная Revolute4, не устраняется из пространства состояний, когда цикл сокращается.

  1. Установите аналитический режим на Trimming. Режим Trimming вставляет подсистему и выходной блок, который выводит четырехкомпонентный сигнал, представляющий механические ограничения, следующие из замкнутого цикла.

  2. Используйте mech_stateVectorMgr получить вектор состояния системы:

    StateManager = ...
   mech_stateVectorMgr('mech_four_bar_lin/Ground_2');
StateManager.StateNames
ans =      
    'mech_four_bar_lin/Revolute2:R1:Position'
    'mech_four_bar_lin/Revolute3:R1:Position'
    'mech_four_bar_lin/Revolute4:R1:Position'
    'mech_four_bar_lin/Revolute2:R1:Velocity'
    'mech_four_bar_lin/Revolute3:R1:Velocity'
    'mech_four_bar_lin/Revolute4:R1:Velocity'

    Revolute1 является соединением сокращения и отсутствует в списке. Состояния 1, 2, и 3 являются вращательными 2, 3, и 4 угла, соответственно; в то время как состояния 4, 5, и 6 являются вращательными 2, 3, и 4 скорости вращения, соответственно.

  3. Настройте необходимые векторы обрезки:

    x0 = [0;0;0;0;0;0]; ix = [];
u0 = []; iu = [];  

y0 = [0;0;0;0]; 
iy = [1;2;3;4];
dx0 = [0;0;0;0;0;0]; 
idx = [3;6];

    x0 вектор говорит trim команда, чтобы запустить ее поиск равновесия с четырёхзвенника в ее начальной настройке (предположение равновесия вы ввели в рабочую область ранее), и с нулевыми скоростями вращения. Вектор индекса ix устанавливает состояния, которые, в фактическом равновесии, должны сохранить значения заданными в x0. Здесь нет ни одного.

    u0 и iu векторы задают системные входные параметры, но нет ни одного.

    y0 вектор устанавливает начальные значения ограничения выходные параметры, чтобы обнулить. Вектор индекса iy требует, чтобы ограничение выходные параметры в равновесии было равно их начальным значениям (0). Это гарантирует, что решение удовлетворяет механическим ограничениям.

    dx0 вектор задает производные начального состояния. Начальные производные углов (т.е. скорости вращения) и скоростей вращения (т.е. угловые ускорения) обнуляются. Вектор индекса idx указывает, что скорость и ускорение Revolute4 в естественном равновесии должны исчезнуть. Не необходимо ограничить производные других состояний, потому что система имеет только одну независимую степень свободы.

  4. Теперь обрежьте систему:

    [x,u,y,dx] = ...
   trim('mech_four_bar_lin',x0,u0,y0,ix,iu,iy,dx0,idx);

    u вектор пуст. Компоненты y и dx исчезните в допусках, указав, что в равновесии, соответственно, механическим ограничениям удовлетворяют, и производные состояния исчезают. Последние три компонента x исчезните, указав на нулевые скорости вращения в равновесии. Первые три компонента x представляйте естественные углы равновесия (в радианах), измеренный как отклонения от начальной настройки. Угол Revolute4 является-0.2395 рад =-13.7o от начальной точки.

    От x, можно вычислить все угловые значения. Естественное равновесие является αeq =-90o - 13.7o =-103.7o, βeq = 310.1o + 13.0o = 323.1o, γeq = 60.3o + 2.5o = 62.8o, и δeq = 360o - αeq - βeq - γeq = 74.7o.

Линеаризация модели в естественном равновесии

Можно теперь линеаризовать систему в этой точке для обрезки.

  1. Сбросьте углы в своей рабочей области к естественной точке равновесия:

    alpha = alpha + x(3); beta = beta + x(2); gamma = gamma + x(1);
delta = 2*pi - alpha - beta - gamma; beta2 = pi - gamma - delta;
delta2 = pi - delta;

  2. Возвратите аналитический режим к Forward Dynamics и обновите схему. Запустите модель, чтобы проверять, что механизм действительно не перемещается.

  3. Чтобы получить нетривиальную линеаризовавшую модель, вам нужны по крайней мере один вход и один выход. Соедините Объединенный Привод с Revolute4, чтобы привести в движение его с крутящим моментом. Затем вставьте Simulink Inport и блоки Выходного порта, чтобы ввести крутящий момент и измерить скорость вращения.

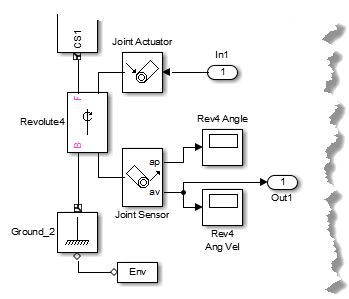
  4. Обнулите входной крутящий момент и начальное состояние к начальной настройке модели, естественному равновесию:

    u = 0; x = [0;0;0;0;0;0];

  5. Линеаризуйте модель и используйте minreal устранить избыточные состояния:

    [A,B,C,D] = linmod('mech_four_bar_lin',x,u); 
[a,b,c,d] = minreal(A,B,C,D);

    оставляя два состояния, α и dα/dt. a компонента (2,1) =-80.1 <0, указывая, что это естественное равновесие устойчиво. Линеаризовавшим движением управляет d2α/dt2 = a (2,1) *α.

Для получения дополнительной информации о пространстве состояний и линеаризации

Смотрите Линеаризацию Открытой Топологии: Двойной Маятник для больше о линеаризовавшем представлении пространства состояний.

Документация Simscape Multibody
Поддержка
Для просмотра документации необходимо авторизоваться на сайте