ncfmargin

Вычислите нормированный взаимно-простой запас устойчивости обратной связи контроллера объекта

Синтаксис

[marg,freq] = ncfmargin(P,C)

[marg,freq] = ncfmargin(P,C,sign)

[marg,freq] = ncfmargin(___,tol)

Описание

[marg,freq] = ncfmargin(P,C) возвращает нормированный взаимно-простой запас устойчивости многомерной обратной связи, состоящей из контроллера C в отрицательной обратной связи с объектом P:

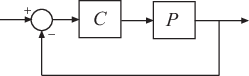
Нормированный взаимно-простой устойчивый запас устойчивости (также названный метрическим запасом устойчивости разрыва) является индикацией относительно робастности к неструктурированным возмущениям. Значения, больше, чем 0,3 обычно, указывают на хорошие поля робастности.

[marg,freq] = ncfmargin(P,C,sign) задает знак связи обратной связи, принятой для граничного вычисления. По умолчанию, sign = -1. Установите sign = +1 для соединения положительной обратной связи.

[marg,freq] = ncfmargin(___,tol) вычисляет нормированную взаимно-простую факторную метрику с заданной относительной точностью.

Примеры

свернуть все

Нормированный взаимно-простой запас устойчивости

Скрипт Open Live Script

Рассмотрите нестабильный объект первого порядка, p, стабилизированный высоким усилением и контроллерами низкого усиления, cL и cH.

p = tf(4,[1 -0.001]); 	
cL = 1;				
cH = 10;

Вычислите запас устойчивости системы с обратной связью с контроллером низкого усиления.

[margL,~] = ncfmargin(p,cL)

margL = 0.7069

Точно так же вычислите запас устойчивости системы с обратной связью с контроллером высокого усиления.

[margH,~] = ncfmargin(p,cH)

margH = 0.0995

Системы с обратной связью с низким усилением и контроллерами высокого усиления нормировали взаимно-простые запасы устойчивости приблизительно 0,71 и 0.1, соответственно. Этот результат показывает, что система с обратной связью с контроллером низкого усиления более устойчива к неструктурированным возмущениям, чем система с контроллером высокого усиления.

Чтобы наблюдать это различие в робастности, создайте неопределенный объект, punc, это имеет дополнительную несмоделированную динамику в высокой частоте по сравнению с номинальным объектом.

punc = p + ultidyn('uncstruc',[1 1],'Bound',1);
sigma(p,punc,'r--')

Вычислите устойчивую устойчивость систем с обратной связью, сформированных неопределенным объектом и каждым контроллером.

[stabmargL,~] = robstab(feedback(punc,cL))

stabmargL = struct with fields:
           LowerBound: 0.9980
           UpperBound: 1
    CriticalFrequency: Inf

[stabmargH,~] = robstab(feedback(punc,cH))

stabmargH = struct with fields:
           LowerBound: 0.0998
           UpperBound: 0.1000
    CriticalFrequency: Inf

Как ожидалось устойчивый анализ устойчивости показывает, что система с обратной связью с контроллером низкого усиления более надежно устойчива в присутствии несмоделированной динамики LTI. На самом деле эта система с обратной связью может терпеть почти 100% заданной неопределенности. В отличие от этого система с обратной связью с контроллером высокого усиления может терпеть только приблизительно 10% заданной неопределенности.

Вычислите метрику разрыва и запас устойчивости

Скрипт Open Live Script

Рассмотрите объект и стабилизировавшийся контроллер.

P1 = tf([1 2],[1 5 10]);
C = tf(4.4,[1 0]);

Вычислите запас устойчивости для этого объекта и контроллера.

b1 = ncfmargin(P1,C)

b1 = 0.1961

Затем вычислите разрыв между P1 и встревоженный объект, P2.

P2 = tf([1 1],[1 3 10]);
[gap,nugap] = gapmetric(P1,P2)

gap = 0.1391

nugap = 0.1390

Поскольку запас устойчивости b1 = b(P1,C) больше разрыва между этими двумя объектами, C также стабилизирует P2. Как обсуждено в Метриках Разрыва и Запасах устойчивости, запасе устойчивости b2 = b(P2,C) удовлетворяет неравенству asin(b(P2,C)) ≥ asin(b1)-asin(gap). Подтвердите этот результат.

b2 = ncfmargin(P2,C);
[asin(b2) asin(b1)-asin(gap)]

ans = 1×2

    0.0997    0.0579

Входные параметры

свернуть все

`P` — Объект
модель динамической системы

Объект, заданный как модель динамической системы. P может быть SISO или MIMO, настолько же долго как P*C имеет то же количество вводов и выводов. P может быть непрерывное время или дискретное время. Если P обобщенная модель в пространстве состояний (genss или uss) затем ncfmargin использует текущее значение или номинальную стоимость всех блоков системы управления в P.

`C` — Контроллер
модель динамической системы

Объект, заданный как модель динамической системы. C может быть SISO или MIMO, настолько же долго как P*C имеет то же количество вводов и выводов. C может быть непрерывное время или дискретное время. Если C обобщенная модель в пространстве состояний (genss или uss) затем ncfmargin использует текущее значение или номинальную стоимость всех блоков системы управления в P.

По умолчанию, ncfmargin принимает соединение отрицательной обратной связи между P и C. Чтобы вычислить поля для системы с обратной связью с положительной обратной связью, используйте [marg,freq] = ncfmargin(P,C,+1).

`sign` — Знак обратной связи
-1 (значение по умолчанию) | `+1`

Знак связи обратной связи, заданной как любой -1 или +1.

Значение по умолчанию, sign = -1, задает отрицательную обратную связь. Установка sign = +1 принимает связь положительной обратной связи для граничного вычисления, как в следующей схеме.

`tol` — Относительная точность
0,001 (значения по умолчанию) | положительная скалярная величина меньше чем 1

Относительная точность для вычисленного поля, заданного как значение положительной скалярной величины меньше чем 1. Значение по умолчанию 0.001, или точность на 0,1%.

Выходные аргументы

свернуть все

`marg` — Нормированный взаимно-простой устойчивый запас устойчивости
скаляр в [0,1]

Нормированный взаимно-простой устойчивый запас устойчивости, возвращенный как скаляр в области значений [0,1]. Это количество, также известное как метрический запас устойчивости разрыва, является индикатором робастности с обратной связью к неструктурированным возмущениям. Для архитектуры управления отрицательной обратной связи Это задано как:

$b (P, C) = {‖ [\begin{matrix} I \\ C \end{matrix}] {(I + P C)}^{- 1} [\begin{matrix} I & P \end{matrix}] ‖}_{\infty}^{- 1} = {‖ [\begin{matrix} I \\ P \end{matrix}] {(I + C P)}^{- 1} [\begin{matrix} I & C \end{matrix}] ‖}_{\infty}^{- 1} .$

Значения, больше, чем 0,3 обычно, указывают на хорошие поля робастности. Если система с обратной связью нестабильна, то marg = 0. Количество b (P, C) ^–1 является усилением сигнала от воздействий на вводе и выводе объекта к вводу и выводу контроллера.

`freq` — Частота, на которой происходит поле
скаляр | `NaN`

Частота, в который граничный marg происходит, возвращенный как скаляр. Если система с обратной связью нестабильна, то freq = NaN.

Больше о

свернуть все

Запас устойчивости и метрики разрыва

b запаса устойчивости (P, C) связан с метрикой разрыва, которая дает численное значение δ (P ₁, P ₂) для расстояния между двумя системами LTI (см. gapmetric).

И для разрыва и для ν - метрики разрыва, следующий устойчивый результат производительности содержит:

arcsin b (P ₂, C ₂) ≥ arcsin b (P ₁, C ₁) – arcsin δ (P ₁, P ₂) – arcsin δ (C ₁, C ₂),

Чтобы интерпретировать этот результат, предположите, что номинальный объект P ₁ стабилизируется контроллером C ₁ с запасом устойчивости b (P ₁, C ₁). Затем если P ₁ встревожен к P ₂, и C ₁ встревожен к C ₂, запас устойчивости ухудшается не больше, чем вышеупомянутой формулой.

ν - разрыв всегда меньше чем или равен разрыву, таким образом, его прогнозы с помощью вышеупомянутого результата робастности более трудны.

Советы

В то время как ncfmargin принимает цикл отрицательной обратной связи, ncfsyn команда проектирует контроллер для цикла положительной обратной связи. Поэтому вычислить поле с помощью контроллера, спроектированного с ncfsyn, используйте [marg,freq] = ncfmargin(P,C,+1).

Алгоритмы

Расчет нормированного взаимно-простого запаса устойчивости как описано в Главе 16 [1].

Ссылки

[1] Чжоу, K., Дойл, J.C., основы устойчивого управления. Лондон, Великобритания: Пирсон, 1997.

Документация

ncfmargin

Синтаксис

Описание

Примеры

Нормированный взаимно-простой запас устойчивости

Вычислите метрику разрыва и запас устойчивости

Входные параметры

`P` — Объект
модель динамической системы

`C` — Контроллер
модель динамической системы

`sign` — Знак обратной связи
-1 (значение по умолчанию) | `+1`

`tol` — Относительная точность
0,001 (значения по умолчанию) | положительная скалярная величина меньше чем 1

Выходные аргументы

`marg` — Нормированный взаимно-простой устойчивый запас устойчивости
скаляр в [0,1]

`freq` — Частота, на которой происходит поле
скаляр | `NaN`

Больше о

Запас устойчивости и метрики разрыва

Советы

Алгоритмы

Ссылки

Смотрите также

Представлено до R2006a

Документация Robust Control Toolbox

Поддержка

Документация

ncfmargin

Синтаксис

Описание

Примеры

Нормированный взаимно-простой запас устойчивости

Вычислите метрику разрыва и запас устойчивости

Входные параметры

P — Объект модель динамической системы

C — Контроллер модель динамической системы

sign — Знак обратной связи-1 (значение по умолчанию) | +1

tol — Относительная точность 0,001 (значения по умолчанию) | положительная скалярная величина меньше чем 1

Выходные аргументы

marg — Нормированный взаимно-простой устойчивый запас устойчивости скаляр в [0,1]

freq — Частота, на которой происходит поле скаляр | NaN

Больше о

Запас устойчивости и метрики разрыва

Советы

Алгоритмы

Ссылки

Смотрите также

Представлено до R2006a

Документация Robust Control Toolbox

Поддержка

`P` — Объект
модель динамической системы

`C` — Контроллер
модель динамической системы

`sign` — Знак обратной связи
-1 (значение по умолчанию) | `+1`

`tol` — Относительная точность
0,001 (значения по умолчанию) | положительная скалярная величина меньше чем 1

`marg` — Нормированный взаимно-простой устойчивый запас устойчивости
скаляр в [0,1]

`freq` — Частота, на которой происходит поле
скаляр | `NaN`