Пример 1

Количественное выражение упрощено автоматически:

3 * x * y * (1/18) * sin(4) * 4

Упорядоченное расположение условий продукта является не обязательно тем же самым как на входе:

x * y * 3 * z * a * b * c

Внутренне, этим продуктом является символьный вызов _mult:

op(%, 0), type(%)

Обратите внимание на то, что экран выход не обязательно отражает внутренний порядок условий в продукте:

op(%2)

В частности, числовой фактор внутренне хранится как последний операнд. На экране числовой фактор отображен перед остающимися условиями:

3 * x * y * 4

op(%)

Пример 2

Функциональный эквивалент _mult из оператора * удобный инструмент для вычисления конечных продуктов. В следующем условия сгенерированы через оператор последовательности $:

_mult(i $ i = 1..20)

Например, легко умножить все элементы в наборе:

S := {a, b, 1, 2, 27}: _mult(op(S))

Следующая команда “архивирует” два списка путем умножения соответствующих элементов:

L1 := [1, 2, 3]: L2 := [a, b, c]: zip(L1, L2, _mult)

delete S, L1, L2:

Пример 3

Полиномы типа DOM_POLY умножаются на *, если у них есть тот же indeterminates и тот же содействующий звонок:

poly(x^2 + 1, [x]) * poly(x^2 + x - 1, [x])

Если indeterminates или содействующие звонки не соответствуют, _mult возвращает ошибку:

poly(x, [x]) * poly(x, [x, y])

Error: Invalid argument. [_mult]

poly(x, [x]) * poly(x, [x], Dom::Integer)

Error: Invalid argument. [_mult]

Используя *, можно умножить полиномы на скалярные факторы:

2 * y * poly(x, [x])

Используйте multcoeffs вместо этого:

multcoeffs(poly(x^2 - 2, [x]), 2*y)

Пример 4

Для конечных множеств XY, продукт X * Y набор:

{a, b, c} * {1, 2}

Обратите внимание на то, что комплексные числа типа DOM_INT, DOM_RAT, DOM_COMPLEX, DOM_FLOAT, и идентификаторы неявно преобразованы в наборы с одним элементом:

2 * {a, b, c}

a * {b, c}, PI * {3, 4}

Пример 5

Умножение на константное выражение выполняется с обеих сторон уравнения:

(a = b) * c

Для неравенств только выполняется этот шаг, если константа, как известно, ненулевая:

assume(d <> 0):
(a <> b) * c, (a <> b) * d;
delete d:

Умножение сравнения с константой только задано для вещественных чисел. Даже для них, результат зависит от знака константы, начиная с умножения с отрицательной константой изменения направление сравнения:

(a < b) * 2, (a < b) * (-3)

(a < b) * I

Error: Inequalities must not be multiplied by complex numbers. [_less::_mult]

(a < b) * c, (a <= b) * c

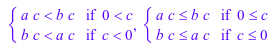
Умножение двух равенств выполняется путем умножения левых сторон и правых сторон отдельно:

(a = b) * (c = d)

Неравенства не могут быть умножены друг с другом или со сравнениями; умножение с равенствами, однако, задано, если по крайней мере один операнд уравнения, как известно, является ненулевым:

assume(d <> 0):
(a <> b) * (c = d);
delete d:

В других случаях не расширен продукт:

delete c, d:
(a <> b) * (c = d)

Умножение сравнений с равенствами и сравнений выполняется похожее на случаи выше:

assume(c > 0):
(a < b) * (c = d);
delete c:

(a <= b) * (c <= d)

Пример 6

Различные области библиотеки, такие как матричная перегрузка областей _mult. Умножение не является коммутативным:

x := Dom::Matrix(Dom::Integer)([[1, 2], [3, 4]]):
y := Dom::Matrix(Dom::Rational)([[10, 11], [12, 13]]):
x * y, y * x

Если условия в x * y имеют другой тип, первый срок x попытки преобразовать y к типу данных x. Если успешный, продукт имеет тот же тип как x. В предыдущем примере, x и y имейте различные типы (оба - матрицы, но области компонента отличаются). Следовательно x * y и y * x имейте различные типы, который наследован от первого срока:

domtype(x * y), domtype(y * x)

Если x не успешно выполняется, чтобы преобразовать y, затем y попытки преобразовать x. В следующем вызове, 27/2 компонента не может быть преобразован в целое число. Следовательно, в x * y, термин y преобразует x и приводит к результату, который совпадает с доменным типом y:

y := Dom::Matrix(Dom::Rational)([[10, 11], [12, 27/2]]):
x * y, y * x

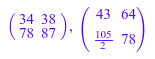
domtype(x * y), domtype(y * x)

delete x, y:

Пример 7

Этот пример демонстрирует, как реализовать slot"_mult" для области. Следующий доменный myString должен представлять символьные строки. Через перегрузку _mult, целочисленные множители таких строк должны произвести конкатенацию соответствующего количества копий строки.

"new" метод использует expr2text чтобы преобразовать любой MuPAD^® возражают против строки. Эта строка является внутренним представлением элементов myString. "print" метод превращает эту строку в экран выход:

myString := newDomain("myString"):
myString::new := proc(x)
begin
  if args(0) = 0 then x := "": end_if;
  case domtype(x)
    of myString do return(x);
    of DOM_STRING do return(new(dom, x));
    otherwise return(new(dom, expr2text(x)));
  end_case
end_proc:
myString::print := x -> extop(x, 1):

Без "_mult" метод, системная функция _mult элементы указателей этой области как любой символьный объект:

y := myString(y):
z := myString(z):
4 * x * y * z * 3/2

Теперь мы реализуем "_mult" метод. Это использует split выбрать все целочисленные условия в его списке аргументов и умножает их. Результатом является целочисленный n. Если существует точно еще один оставленный термин (это должно быть строкой типа myString), это - скопированный n \times. Конкатенация копий возвращена:

myString::_mult:= proc()
local Arguments, intfactors, others, dummy, n;
begin
  print(Unquoted, "Info: myString::_mult called with the arguments:",
           args());
  Arguments := [args()];
  // split the argument list into integers and other factors:
  [intfactors, others, dummy] := 
      split(Arguments, testtype, DOM_INT);
  // multiply all integer factors:
  n := _mult(op(intfactors));
  if nops(others) <> 1 then
     return(FAIL)
  end_if;
  myString::new(_concat(extop(others[1], 1) $ n))
end_proc:

Теперь целочисленные множители myString объекты могут быть созданы через * оператор:

2 * myString("string") * 3

Info: myString::_mult called with the arguments:, 2, string, 3

Только продукты целых чисел и myString объекты позволены:

3/2 * myString("a ") * myString("string")

                                                  3
Info: myString::_mult called with the arguments:, -, a , string
                                                  2

delete myString, y, z:

Возвращаемые значения

Арифметическое выражение, полином, набор, уравнение, неравенство или сравнение.

Перегруженный

xY