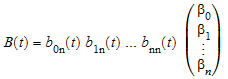bernsteinMatrixМатрица Бернстайна
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
bernsteinMatrix(n, t)
bernsteinMatrix(n, t), где t вектор длины m, возвращает m- (n+1) Матрица Бернстайна M, таким образом, что M(i,k+1) = binomial(n,k)*t[i]^k*(1-t[i])^(n-k). Здесь, индекс i запуски от 1 до m, и индекс k запуски от 0 к n. Смотрите пример 2 и пример 3.
Матрица Бернстайна также называется матрицей Безье.
Используйте матрицы Бернстайна, чтобы создать Кривые Безье:
bezierCurve = bernsteinMatrix(n, t)*P
P задайте контрольные точки Кривой Безье. Например, чтобы создать 3-D Кривую Безье второго порядка, задайте контрольные точки как:P = [p0x, p0y, p0z; p1x, p1y, p1z; p2x, p2y, p2z]
Постройте четвертый порядок 2-D Кривая Безье, заданная контрольными точками p0 = [0, 1], p1 = [4, 3], p2 = [6, 2], p3 = [3, 0], p4 = [2, 4]. Создайте матрицу с каждой строкой, представляющей контрольную точку:
P := matrix([[0, 1], [4, 3], [6, 2], [3, 0], [2, 4]]):
Создайте четвертый порядок матрица Бернстайна B:
B := bernsteinMatrix(4, t)
![]()
Создайте Кривую Безье:
bezierCurve := simplify(B*P)
![]()
Постройте точки кривой и контрольные точки:
plot(plot::PointList2d(P),
plot::Curve2d(bezierCurve, t = 0..a, a = 0..1))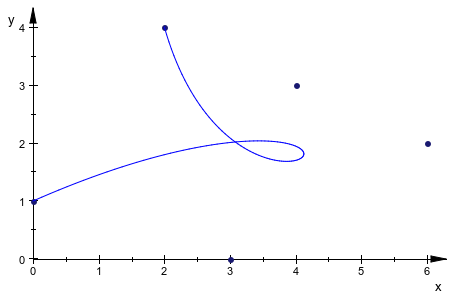
Создайте третий порядок 3-D Кривая Безье, заданная 3х3 матричным P из контрольных точек. Каждая контрольная точка соответствует строке матричного P.
P := matrix([[0, 0, 0], [2, 2, 2], [2, -1, 1], [6, 1, 3]]):
Создайте матрицу Бернстайна:
B := bernsteinMatrix(3, t)
![]()
Создайте Кривую Безье:
bezierCurve := simplify(B*P)
![]()
Постройте контрольные точки и Кривую Безье:
plot(plot::PointList3d(P),
plot::Curve3d(bezierCurve, t = 0..a, a = 0..1))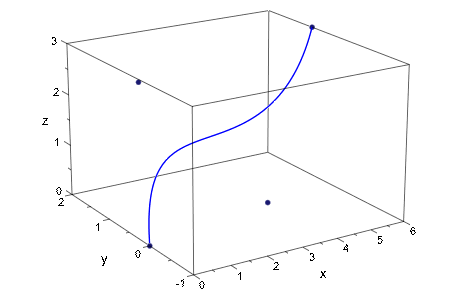
|
Неотрицательное целое число. |
|
Арифметическое выражение, список выражений или вектор выражений. В MuPAD®, |
nops(t)⨉(n+1) матрица доменного типа Dom::Matrix().
Полином Бернстайна степени n определяется следующим образом:
![]()
Здесь,
![]()
базисные полиномы Бернстайна, и
![]()
Коэффициенты
![]()
Полином Бернстайна дан умножением матриц матрицы Бернстайна и вектором коэффициентов: