`bernstein`

Полиномы Бернстайна

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

bernstein(f, n, t)
bernstein(g, <var>, n, t)

Описание

bernstein(n, f, t) с одномерным функциональным f возвращает nth-порядок полином Бернстайна sum(binomial(n,k)*t^k*(1-t)^(n-k)*f(k/n),k = 0..n) оцененный в точке t. Этот полином является приближением f на интервале [0,1]. Смотрите пример 1.

bernstein(g, <var>, n, t) с символьным выражением g возвращает nth-порядок полиномиальное приближение Бернстайна g, оцененный в точке t. Этот синтаксис расценивает g как одномерная функция переменной var. Можно не использовать определение переменной var если выражение g является одномерным. Если это многомерно, необходимо задать var. Смотрите пример 2 и пример 3.

Представление Бернстайна полинома численно устойчиво при замене численными значениями между 0 и 1 для t. Тем не менее, если вы упрощаете полином Бернстайна, результат может быть нестабильным при заменении численными значениями t. Смотрите пример 4.

Примеры

Пример 1

Задайте функцию, представляющую линейный пандус как функция MuPAD^®:

f := t -> triangularPulse(1/4, 3/4, infinity, t):

Аппроксимированный f согласно пятому порядку полиномы Бернстайна в переменной t:

b5 := bernstein(f, 5, t)

Пример 2

Аппроксимируйте синусоидальную функцию sin(2*PI*t) 10-м и 100-й степенью полиномы Бернстайна:

b10 := bernstein(sin(2*PI*t), 10, t):
b100 := bernstein(sin(2*PI*t), 100, t):

Постройте sin(2*pi*t) и его приближения:

p1 := plot::Function2d(sin(2*PI*t), t = 0..1,
                      LegendText = "sine function",
                      Color = RGB::Red):
p2 := plot::Function2d(b10, t = 0..1,
                      LegendText = "10th degree polynomial",
                      Color = RGB::Green):
p3 := plot::Function2d(b100, t = 0..1,
                      LegendText = "100th degree polynomial",
                      Color = RGB::Blue):
plot(p1, p2, p3, LegendVisible = TRUE)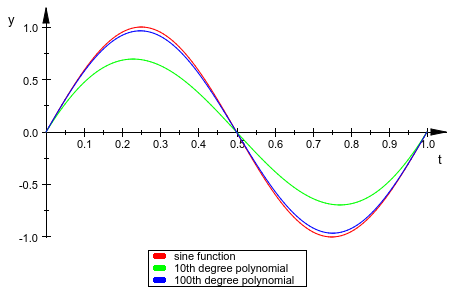

Пример 3

Аппроксимируйте показательную функцию полиномом Бернстайна второго порядка в переменной t:

bernstein(exp(x), 2, t)

Аппроксимируйте многомерную показательную функцию y*exp(x*y). Необходимо задать переменную, потому что это выражение содержит больше чем одну переменную. bernstein рассматривает выражение как одномерную функцию той переменной. Например, чтобы обработать это выражение как одномерную функцию x, Введите:

bernstein(y*exp(x*y), x, 2, t)

Обрабатывать это выражение как одномерную функцию y, Введите:

bernstein(y*exp(x*y), y, 2, t)

Пример 4

Когда вы упрощаете старший символьный полином Бернстайна, результат часто не может оцениваться численно устойчивым способом.

Аппроксимируйте эту функцию меандра 100-й степенью полином Бернстайна, и затем упростите результат:

f := rectangularPulse(1/4,3/4,t):
f1 := bernstein(f, 100, t):
f2 := simplify(f1):

Сравните график исходной функции меандра f, его численно устойчивое представление Бернстайна f1, и его упрощенная версия f2. Упрощенная версия показывает область числовой нестабильности.

plot(f, f1, f2, t = 0..1)

Параметры

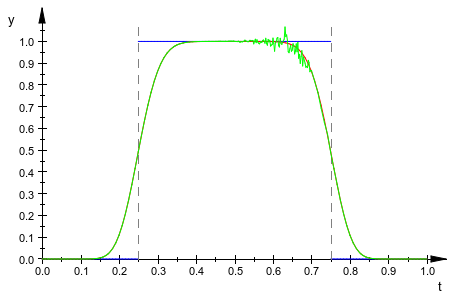
`n`	Неотрицательное целое число.
`f`	Функция, принимающая один входной параметр и возвращающая арифметическое выражение.
`g`	Арифметическое выражение.
`t`	Арифметическое выражение.
`var`	Неопределенный, заданный как идентификатор или индексированный идентификатор.