daetools::findDecoupledBlocksИщите разъединенные блоки в системах уравнений
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
[eqsBlocks,varsBlocks] := daetools::findDecoupledBlocks(eqs,vars)
[eqsBlocks,varsBlocks] := daetools::findDecoupledBlocks(eqs,vars) идентифицирует подмножества (блоки) уравнений, которые могут использоваться, чтобы задать подмножества переменных. Количество переменных vars должен совпасть с количеством уравнений eqs.
iблок th является системой уравнений, определяющей переменные в vars[varsBlocks[i]]. Переменные в vars[varsBlocks[1],...,varsBlocks[i-1]] определяются рекурсивно предыдущими блоками уравнений. После того, как вы решаете первый блок уравнений для первого блока переменных, второго блока уравнений, данных eqs[eqsBlocks[2]], задает разъединенное подмножество уравнений, содержащих только подмножество переменных, данных вторым блоком переменных vars[varsBlock[2]], плюс переменные из первого блока (эти переменные известны в это время). Таким образом, если нетривиальная блочная декомпозиция возможна, можно разделить процесс решения для большой системы уравнений, включающей много переменных в несколько шагов, где каждый шаг включает меньшую подсистему.
Количеством блоков является nops(eqsBlocks). Это совпадает с nops(varsBlocks). Если nops(eqsBlocks) = nops(varsBlocks) = 1, затем нетривиальная блочная декомпозиция уравнений не возможна.
Реализованный алгоритм требует этого для каждой переменной в vars в eqs должно быть по крайней мере одно соответствующее уравнение включение этой переменной. То же уравнение не может также быть соответствующим к другой переменной. Если система не удовлетворяет этому условию, то daetools::findDecoupledBlocks выдает ошибку. В частности, daetools::findDecoupledBlocks требует того nops(eqs) = nops(vars).
Вычислите блок нижнее треугольное разложение символьной системы дифференциальных алгебраических уравнений (ДАУ).
Создайте следующую систему четырех дифференциальных алгебраических уравнений. Здесь, выражения x1(t), x2(t), x3(t), и x4(t) представляйте переменные состояния системы. Система также содержит символьные параметры c1C2 , c3, c4, и выражения f(t,x,y) и g(t,x,y).
eqs := [c1*diff(x1(t),t) + c2*diff(x3(t),t) = c3*f(t,x1(t),x3(t)),
c2*diff(x1(t),t) + c1*diff(x3(t),t) = c4*g(t,x3(t),x4(t)),
x1(t) = g(t,x1(t),x3(t)),
x2(t) = f(t,x3(t),x4(t))]:
vars:= [x1(t), x2(t), x3(t), x4(t)]:Используйте daetools::findDecoupledBlocks найти блочную структуру системы.
[eqsBlocks, varsBlocks] := daetools::findDecoupledBlocks(eqs, vars)
![]()
Первый блок содержит два уравнения в двух переменных.
eqs[eqsBlocks[1]]
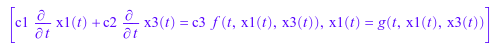
vars[varsBlocks[1]]
![]()
После того, как вы решаете этот блок для переменных состояния x1(t), x3(t), можно решить следующий блок уравнений. Этот блок состоит из одного уравнения.
eqs[eqsBlocks[2]]
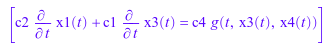
Этот блок включает одну переменную.
vars[varsBlocks[2]]
![]()
После того, как вы решаете уравнение от блока 2 для переменной состояния x4(t), оставшийся блок уравнений eqs[eqsBlocks[3]] задает остающуюся переменную vars[varsBlocks[3]].
eqs[eqsBlocks[3]]; vars[varsBlocks[3]]
![]()
![]()
Найдите сочетания, которые преобразуют систему в блок нижняя треугольная форма.
eqsPerm := [op(eqsBlocks[i]) $ i = 1..nops(eqsBlocks)]; varsPerm := [op(varsBlocks[i]) $ i = 1..nops(varsBlocks)]
![]()
![]()
Преобразуйте систему в блок нижняя треугольная система уравнений.
eqs := eqs[eqsPerm]; vars := vars[varsPerm]
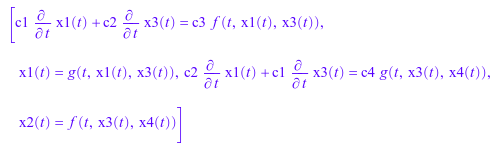
![]()
Найдите матрицу падения получившейся системы. Матрица падения показывает, что система переставленных уравнений имеет три диагональных блока размера 2- 2, 1- 1, и 1- 1.
daetools::incidenceMatrix(eqs, vars)

|
Список или вектор уравнений или выражений в переменных состояния |
|
Список или вектор идентификаторов или выражений, таких как |
Вложенный список целых чисел, представляющих сочетания, требуемые преобразовывать исходную систему eqs,vars с блоком нижняя треугольная форма.