detОпределитель матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
det(A, options)
det(A) возвращает определитель матричного A.
Если входной матрицей является array из доменного типа DOM_ARRAY, затем numeric::det(A, Symbolic) называется, чтобы вычислить результат.
Определитель hfarrays доменного типа DOM_HFARRAY внутренне вычисляется через numeric::det(A).
Если аргумент не оценивает к матрице одного из упомянутых выше типов, символьный вызов det(A) возвращен.
MinorExpansion опция полезна для маленьких матриц (обычно, матриц размерности до 10) содержащий много символьных записей. По умолчанию, det попытки распознать матрицы, которые могут извлечь выгоду из использования MinorExpansion, и использование эта опция при вычислении их определителей. Тем не менее, det не всегда распознает эти матрицы. Кроме того, идентификация, что матрица мала достаточно и содержит много символьных записей, занимает время. Чтобы улучшать производительность, используйте MinorExpansion опция явным образом.
По умолчанию, det вызовы normal прежде, чем возвратить результаты. Этот дополнительный внутренний вызов гарантирует, что конечный результат нормирован. Этот вызов может быть в вычислительном отношении дорогим. Это также влияет на результат, возвращенный det только если матрица содержит переменные или точные выражения, такие как sqrt(5) или sin(PI/7).
Чтобы избежать этого дополнительного вызова, задайте Normal = FALSE. В этом случае, det также может возвратить нормированные результаты, но не гарантирует такой нормализации. Смотрите Пример 3 и Пример 4.
Мы вычисляем определитель матрицы, данной различными типами данных:
A := array(1..2, 1..2, [[1, 2], [3, PI]]); det(A)
![]()
![]()
B := hfarray(1..2, 1..2, [[1, 2], [3, PI]]); det(B)
![]()
![]()
C := matrix(2, 2, [[1, 2], [3, PI]]); det(C)
![]()
![]()
delete A, B, C:
Если вход не оценивает к матрице, то на символьные звонки отвечают:
delete A, B: det(A + 2*B)
![]()
Если вы используете Normal опция, det вызывает normal функция для конечных результатов. Этот вызов гарантирует тот det возвращает результаты в нормированной форме:
det(matrix([[x, x^2], [x/(x + 2), 1/x]]))
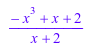
Если вы задаете Normal = FALSEdet не вызывает normal для конечного результата:
det(matrix([[x, x^2], [x/(x + 2), 1/x]]), Normal = FALSE)
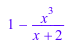
Используя Normal может значительно уменьшить производительность det. Например, вычисление определителя этой матрицы занимает много времени:
n := 5:
det5 := det(matrix([[(x[i*j]^(i + j) + x[i+j]^j)/(i + j) $
j = 1..n] $
i = 1..n])):Для лучшей производительности задайте Normal = FALSE:
n := 5:
det5 := det(matrix([[(x[i*j]^(i + j) + x[i+j]^j)/(i + j) $
j = 1..n] $
i = 1..n]),
Normal = FALSE):
|
Квадратная матрица: любой двумерный |
|
Вычислите определитель рекурсивным незначительным расширением вдоль первого столбца. |
|
Опция, заданная как Возвратите нормированные результаты. Значение |
Арифметическое выражение.
A