Нормируйте выражение
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
normal(f,options) normal(object)
normal(f) возвращает нормальную форму рационального выражения f. MuPAD® расценивает выражение, как нормировано, когда это - часть, где и числитель и знаменатель являются полиномами, наибольший общий делитель которых равняется 1.
normal(object) заменяет операнды object с их нормированной формой.
normal и simplifyFraction эквивалентны.
Если аргумент f содержит иррациональные подвыражения, такие как sin(x), x^(-1/3) и т.д. затем они заменяются вспомогательными переменными перед нормализацией. После нормализации эти переменные заменяются нормализацией исходных подвыражений. Алгебраические зависимости подвыражений не учтены. Операнды нерациональных подвыражений нормированы рекурсивно.
Если аргумент f содержит числа с плавающей запятой, затем они заменяются рациональными аппроксимирующими функциями (см. numeric::rationalize). В конце, float применяется к результату.
С Expand опция, нормальная форма уникальна для рациональных выражений: это - частное расширенных полиномов, наибольший общий делитель которых равняется 1. Если f и g рациональные выражения, следующие операторы эквивалентны:
f и g математически эквивалентны.
normal(f, Expand) = normal(g, Expand)
normal(f - g, Expand) = 0
Нормальная форма сгенерирована без Expand опция (который эквивалентен Expand = FALSE) частное продуктов степеней расширенных полиномов, где все факторы числителя и знаменателя являются взаимно-простыми. MuPAD расценивает разложенные на множители выражения, такие как x (x + 1), и эквивалентные расширенные выражения, такие как x 2 + x, как нормировано. Поэтому, если вы не используете Expand, нет никакой уникальной нормальной формы рационального выражения.
Если f и g рациональные выражения, эти операторы эквивалентны:
f и g математически эквивалентны.
normal(f - g) = 0
Для специальных объектов, normal автоматически сопоставлен с его операндами. В частности, если object полином доменного типа DOM_POLY, затем его коэффициенты нормированы. Далее, если object набор, список, таблица или массив, соответственно, затем normal применяется ко всем записям. Далее, левые и правые стороны уравнений (вводят "_equal"), неравенства (вводят "_unequal"), и отношения (вводят "_less" или "_leequal") нормированы. Далее, операнды областей значений (вводят "_range") нормированы автоматически.
Вычислите нормальную форму некоторых рациональных выражений:
normal(x^2 - (x + 1)*(x - 1))
![]()
normal((x^2 - 1)/(x + 1))
![]()
normal(1/(x + 1) + 1/(y - 1))
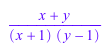
Следующее выражение должно рассматриваться как рациональное выражение в “indeterminates” y и sin(x):
normal(1/sin(x)^2 + y/sin(x))
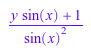
Нормируйте записи этого списка:
[(x^2 - 1)/(x + 1), x^2 - (x + 1)*(x - 1)]
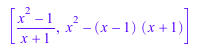
normal(%)
![]()
Теперь нормируйте коэффициенты полиномов:
poly((x^2-1)/(x+1)*Y^2 + (x^2-(x+1)*(x-1))*Y - 1, [Y])
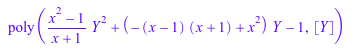
normal(%)
![]()
Если вы используете Expand опция, normal возвращает часть с расширенным числителем и знаменателем:
normal(x/(x^6 - 1) + x^2/(x^4 - 1), Expand)
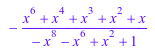
Без Expand, часть возвращена normal может содержать учтенные выражения:
normal(x/(x^6 - 1) + x^2/(x^4 - 1))
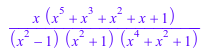
Если вы используете List опция, normal возвращает список, состоящий из числителя и знаменатель входа:
normal((x^2-1)/(x^2+2*x+1), List)
![]()
Обратите внимание на то, что normal(f, List) не то же самое как [numer(f), denom(f)]:
[numer, denom]((x^2-1)/(x^2+2*x+1))
![]()
Чтобы пропустить вычисление общих делителей числителя и знаменателя выражения, используйте NoGcd опция:
y := (x^4 - 1)/(x + 1) + 1: normal(y); normal(y, NoGcd)
![]()
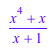
Чтобы задать общие делители, которые вы хотите уравновесить, используйте ToCancel опция:
y := (x^4 - 1)/(x^2 - 1):
normal(y, ToCancel = {x - 1})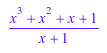
По умолчанию, normal вызывает rationalize функция в попытке рационализировать входное выражение. Вы можете ускорить расчеты при помощи Rationalize = None в сочетании с Expand опция. Эта комбинация опций позволяет вам пропустить занимающиеся расследованиями алгебраические зависимости и, поэтому, экономит некоторое время:
n := exp(u): a := (n^2 + n)/(n + 1) + 1: normal(a, Expand, Rationalize = None)
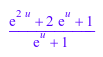
Без Rationalize = None, MuPAD анализирует алгебраические зависимости и возвращает этот результат:
normal(a, Expand)
![]()
Отключите рекурсивные вызовы normal для подвыражений при помощи Recursive = FALSE:
y := sqrt((x^2 + 2*x + 1)/(x + 1)): normal(y, Recursive = FALSE)
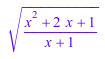
Решите это уравнение и подведите итог пятых степеней решений:
solutions := solve(x^3 + x^2 + 1, x, MaxDegree = 3): f := _plus((solutions[i]^7) $i = 1..3)
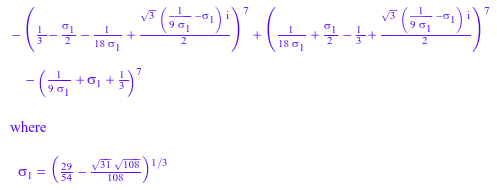
Нормализация результата возвращается:
normal(f)
![]()
Ограничить количество внутренне повторных вызовов normal из-за анализа алгебраических зависимостей, используйте Iterations опция. Количество по умолчанию итераций равняется 5. Используйте Iterations опция, чтобы увеличиться или сократить число итераций. Например, нормируйте результат, использующий всего одну итерацию:
normal(f, Iterations = 1)
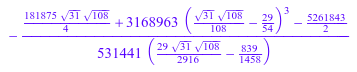
После двух итераций испытывает недостаток результат:
normal(f, Iterations = 2)
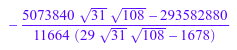
После трех итераций вы получаете самый простой результат:
normal(f, Iterations = 3)
![]()
| |
|
Полином типа |
|
Возвратите числитель и знаменатель нормированного выражения в расширенной форме. См. “Детали” для получения дополнительной информации. По умолчанию, |
|
Возвратите список, состоящий из числителя и знаменатель |
|
Пропустите вычислительные общие делители числителя и знаменатель |
|
Опция, заданная как Уравновесьте только заданные общие делители |
|
Опция, заданная как Выполните только основную рационализацию иррационального входного выражения. Пропустите занимающиеся расследованиями алгебраические зависимости. Эта опция работает только в сочетании с |
|
Рекурсивно нормируйте подвыражения иррационального выражения. По умолчанию, |
|
Опция, заданная как Задайте количество повторных вызовов |
Объект того же типа как входной объект или список двух арифметических выражений, если List опция используется.
object