`linalg`::`kroneckerProduct`

Кронекеров продукт матриц

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

linalg::kroneckerProduct(A, <B, …>)

Описание

linalg::kroneckerProduct(A, B) вычисляет Кронекеров продукт двух матриц A и B.

Кронекеров продукт (прямое матричное произведение) m ×n матричный A и p ×q матричный B (m p) × (n q) матрица, данная в клеточном виде как

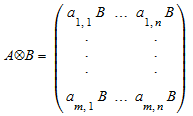Покомпонентно: с I = p (i - 1) + k, J = q (j - 1) + l.

Если A и B матрицы той же матричной области с тем же звонком компонента, результатом является матрица того же типа как A и B. Если области или звонки компонента A и B отличайтесь, linalg::kroneckerProduct попытки преобразовать B в доменный тип A A::dom::coerce. Если это перестало работать, преобразование A к доменному типу B предпринят. Если никакое преобразование не возможно, ошибка повышена.

Примечание

Обратите внимание на то, что Кронекеров продукт только реализован для матриц по областям Dom::Matrix, Dom::SquareMatrix или Dom::MatrixGroup. В частности, это включает матрицы, созданные matrix.

Вызов больше чем с двумя аргументами производит linalg::kroneckerProduct(A, B, C) = linalg::kroneckerProduct(linalg::kroneckerProduct(A, B), C) и т.д.

Вызов только с одним аргументом возможен. Это возвращает входную матрицу.

Примеры

Пример 1

Мы считаем две матрицы A и B с символьными компонентами:

A:= matrix([[a11, a12], [a21, a22]]);
B:= matrix([[b11, b12, b13], [b21, b22, b23]]);

Кронекеров продукт A и B вычисляется путем умножения матричного B с каждым из компонентов матричного A. Получившаяся блочная матрица возвращена как матрица большей размерности:

linalg::kroneckerProduct(A, B);

delete A, B:

Пример 2

n ×n матричный H с компонентами в {-1, 1} называется матрицей Адамара если H умноженный с транспонировать равняется временам n n ×n единичная матрица. Матричный H заданный ниже матрица Адамара:

H:= matrix([[1, 1], [1, -1]]);
H * linalg::transpose(H) = 2 * matrix::identity(2);

Матрицы Адамара играют роль в области кодов с коррекцией ошибок. Основное свойство этого типа матриц состоит в том, что Кронекеровым продуктом двух матриц Адамара является снова матрица Адамара. Мы проверяем этот оператор для матричного H:

H2:= linalg::kroneckerProduct(H, H);

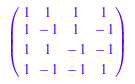
Действительно, матричный H2 снова матрица Адамара:

H2 * linalg::transpose(H2) = 4 * matrix::identity(4);

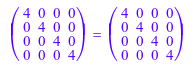
delete H, H2:

Параметры

AB…

Матрицы областей Dom::Matrix, Dom::SquareMatrix или Dom::MatrixGroup

Возвращаемые значения

Матрица того же типа как A или B.

Документация