Пример 1

Мы создаем 2×2 матрица путем передачи списка двух строк к matrix, где каждая строка является списком двух элементов:

A := matrix([[1, 5], [2, 3]])

Таким же образом мы генерируем следующие 2 ×3 матрицы:

B := matrix([[-1, 5/2, 3], [1/3, 0, 2/5]])

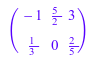
Мы можем сделать матричную арифметику с помощью стандартных арифметических операторов MuPAD. Например, матричным произведением A  B, четвертая степень A и скалярное умножение A дают:

A * B, A^4, 1/3 * A

Начиная с размерностей матриц отличаются A и B, сумма A и B не задана, и MuPAD возвращает сообщение об ошибке:

A + B

Error: Dimensions do not match. [(Dom::Matrix(Dom::ExpressionField()))::_plus]

Вычислить инверсию A, введите:

1/A

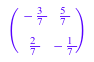
Если матрица не является обратимой, результатом этой операции является FAIL:

C := matrix([[2, 0], [0, 0]])

C^(-1)

delete A, B, C:

Пример 2

В дополнение к стандартной матричной арифметике библиотека linalg предлагает многочисленные функции, обрабатывающие матрицы. Например, функциональный linalg::rank определяет ранг матрицы:

A := matrix([[1, 5], [2, 3]])

linalg::rank(A)

Функциональный linalg::eigenvectors вычисляет собственные значения и собственные вектора A:

linalg::eigenvectors(A)

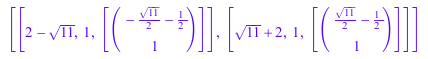
Чтобы определить размерность матрицы, используйте функциональный linalg::matdim:

linalg::matdim(A)

Результатом является список двух положительных целых чисел, количество строки и столбца матрицы.

Используйте info(linalg) получить список доступных функций или ввести ?linalg для получения дополнительной информации об этой библиотеке.

delete A:

Пример 3

К матричным записям можно получить доступ с оператором индекса [ ]:

A := matrix([[1, 2, 3, 4], [2, 0, 4, 1], [-1, 0, 5, 2]])

A[2, 1] * A[1, 2] - A[3, 1] * A[1, 3]

Можно переопределить матричную запись путем присвоения значения ему:

A[1, 2] := a^2: A

Оператор индекса может также использоваться, чтобы извлечь подматрицы. Следующий вызов создает копию субматрицы A, включающего второе и третью строку и первые три столбца A:

A[2..3, 1..3]

Оператор индекса не позволяет заменять субматрицу данной матрицы другой матрицей. Используйте linalg::substitute достигнуть этого.

delete A:

Пример 4

Некоторые системные функции могут быть применены к матрицам. Например, если вы имеете матрицу с символьными записями и хотите иметь все записи в расширенной форме, просто применить функциональный expand:

delete a, b: 
A := matrix([
  [(a - b)^2, a^2 + b^2], 
  [a^2 + b^2, (a - b)*(a + b)]
])

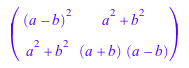
expand(A)

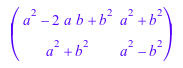
Можно дифференцировать все матричные компоненты относительно некоторых неопределенных:

diff(A, a)

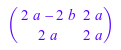
Следующая команда оценивает все матричные компоненты в данной точке:

subs(A, a = 1, b = -1)

Обратите внимание на то, что функциональный subs не оценивает результат замены. Например, мы задаем следующую матрицу:

A := matrix([[sin(x), x], [x, cos(x)]])

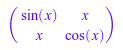
Затем мы заменяем x = 0 в каждом матричном компоненте:

B := subs(A, x = 0)

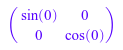
Вы видите, что матричные компоненты не оценены полностью. Например, если вы вводите sin(0) непосредственно, это оценивает, чтобы обнулить.

Функциональный eval может использоваться, чтобы оценить результат функционального subs. Однако eval не работает с матрицами непосредственно, и необходимо использовать функциональный map применять функциональный eval к каждому матричному компоненту:

map(B, eval)

Функциональный zip может быть применен к матрицам. Следующий вызов комбинирует две матрицы A и B путем деления каждого компонента A соответствующим компонентом B:

A := matrix([[4, 2], [9, 3]]): 
B := matrix([[2, 1], [3, -1]]):
A, B, zip(A, B, `/`)

delete A, B:

Пример 5

Вектором является любой m ×1 матрица (вектор-столбец) или 1×n матрица (вектор-строка). Создать вектор с matrix, передайте размерность вектора и список векторных компонентов в качестве аргумента к matrix:

row_vector := matrix(1, 3, [1, 2, 3]); 
column_vector := matrix(3, 1, [1, 2, 3])

Если единственный аргумент matrix невложенный список или одномерный массив, результатом является вектор-столбец:

matrix([1, 2, 3])

Для вектора-строки r, вызовы r[1, i] и r[i] оба возвращают i-th векторный компонент r. Точно так же для вектор-столбца c, вызовы c[i, 1] и c[i] оба возвращают i-th векторный компонент c.

Мы извлекаем второй компонент векторов, заданных выше:

row_vector[2] = row_vector[1, 2],
column_vector[2] = column_vector[2, 1]

Используйте функциональный linalg::vecdim определить количество компонентов вектора:

linalg::vecdim(row_vector), linalg::vecdim(column_vector)

Количество компонентов вектора может также быть определено непосредственно вызовом nops(vector).

Размерность вектора может быть определена аналогичная описанному выше в случае матриц:

linalg::matdim(row_vector),
linalg::matdim(column_vector)

Смотрите linalg пакет для функций, работающих с векторами и страницей справки norm для вычислительных векторных норм.

delete row_vector, column_vector:

Пример 6

Вектором является любой m ×1 матрица (вектор-столбец) или 1×n матрица (вектор-строка). Создать вектор с matrix, можно также передать размерность вектора и таблицу векторных компонентов в качестве аргумента к matrix:

delete v1, v2, t1, t2:
t1 := table():
t1[1,1] := 1:
t1[1,2] := 2:
t1[1,3] := 3:
v1 := matrix(1, 3, t1);

t2 := table():
t2[1,1] := 1:
t2[2,1] := 2:
t2[3,1] := 3:
v2 := matrix(3, 1, t2);

Все функции применились к векторам в предыдущем примере (см. выше), банка может также использоваться на этих векторах.

delete t1, t2, v1, v2:

Пример 7

В следующих примерах мы иллюстрируем различные вызовы matrix аналогичный описанному выше. Мы запускаем путем передачи вложенного списка matrix, где каждый внутренний список соответствует строке матрицы:

matrix([[1, 2], [2]])

Количество строк созданной матрицы является количеством внутренних списков, а именно, m = 2. Количество столбцов определяется максимальным количеством записей внутреннего списка. В примере выше, первый список является самым длинным, и следовательно n = 2. Второй список имеет только один элемент и, поэтому, вторая запись во второй строке возвращенной матрицы была обнулена.

В следующем вызове мы используем тот же вложенный список, но кроме того передаем два параметра размерности, чтобы создать 4×4 матрица:

matrix(4, 4, [[1, 2], [2]])

В этом случае размерность матрицы дана параметрами размерности. Как прежде, недостающие записи во внутреннем списке соответствуют нулю, и кроме того недостающие строки обработаны как нулевые строки.

Если размерность, m ×n матрицы утверждается явным образом, записи, может также быть задана простым списком с m  n элементы. Матрица заполнена этими элементами строка строкой:

matrix(2, 3, [1, 2, 3, 4, 5, 6])

matrix(3, 2, [1, 2, 3, 4, 5, 6])

Пример 8

Один - или двумерный массив арифметических выражений, таких как:

a := array(1..3, 2..4, 
  [[1, 1/3, 0], [-2, 3/5, 1/2], [-3/2, 0, -1]] 
)

может быть преобразован в матрицу можно следующим образом:

A := matrix(a)

Подача массивов, например, как эффективный структурированный тип данных для программирования. Однако массивы не имеют никакого алгебраического значения, и никакие математические операции не заданы для них. Если вы преобразуете массив в матрицу, можно использовать полную функциональность, заданную в матрицах, аналогичных описанному выше. Например, давайте вычислим матрицу 2 A - A ² и норма Фробениуса A:

2*A - A^2, norm(A, Frobenius)

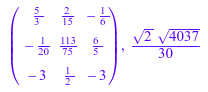
Обратите внимание на то, что массив может содержать неинициализированные записи:

b := array(1..4): b[1] := 2: b[4] := 0: b

matrix не может обработать массивы, которые имеют неинициализированные записи, и отвечает сообщением об ошибке:

matrix(b)

Error: Unable to define a matrix over 'Dom::ExpressionField()'. [(Dom::Matrix(Dom::ExpressionField()))::new]

Мы инициализируем остающиеся записи массива b и преобразуйте его в матрицу, или более точно, в вектор-столбец:

b[2] := 0: b[3] := -1: matrix(b)

delete a, A, b:

Пример 9

Мы показываем, как создать матрицу, компоненты которой заданы функцией строки и индекса столбца. Запись в i-th строка и j-th столбец Гильбертовой матрицы (см. также linalg::hilbert). Таким образом следующая команда создает 2×2 Гильбертова матрица:

matrix(2, 2, (i, j) -> 1/(i + j - 1))

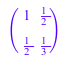
Следующие два вызова приводят к различным результатам. В первом вызове, x рассматривается как неизвестная функция, в то время как это - константа во втором вызове:

delete x:
matrix(2, 2, x), matrix(2, 2, (i, j) -> x)

Пример 10

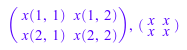
Диагональные матрицы могут быть созданы путем передачи опции Diagonal и список диагональных элементов:

matrix(3, 4, [1, 2, 3], Diagonal)

Можно сгенерировать 3×3 единичная матрица можно следующим образом:

matrix::identity(3)

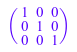
Вот альтернативные способы создать эту матрицу:

matrix(3, 3, [1 $ 3], Diagonal)

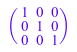
Эквивалентно, можно использовать функцию одного аргумента:

matrix(3, 3, i -> 1, Diagonal)

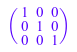
Начиная с целочисленного 1 также представляет постоянную функцию, следующий более короткий вызов создает ту же матрицу:

matrix(3, 3, 1, Diagonal)

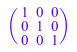
Чтобы продемонстрировать использование таблиц для создания (разреженных) матриц, мы можем также создать единичную матрицу выше линиями:

t := table(): t[1, 1] := 1: t[2, 2] := 1: t[3, 3] := 1:
matrix(3, 3, t)

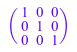
delete t:

Пример 11

Полосные матрицы Теплица могут быть созданы с опцией Banded. Следующая команда создает трехдиагональную матрицу с постоянными полосами:

matrix(4, 4, [-1, 2, -1], Banded)

Пример 12

Матрицы могут также быть созданы при помощи table:

t := table():
t[1, 2] := 12:
t[3, 1] := 31:
t[3, 2] := 32:
t

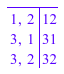
Недостающие записи таблицы соответствуют пустым матричным записям:

A := matrix(4, 6, t)

При помощи таблиц можно легко создать большие (разреженные) матрицы, не будучи обеспеченным, чтобы задать все нулевые записи матрицы. Обратите внимание на то, что это - большое преимущество перед использованием массивов, где каждый компонент должен быть инициализирован прежде.

delete t, A:

Пример 13

Метод "doprint" из Dom::Matrix() печать только ненулевые компоненты разреженной матрицы:

A := matrix(4, 6):
A[1, 2]:= 12: A[3, 1]:= 31: A[3, 2]:= 32:
print(A::dom::doprint(A)):

delete A:

Возвращаемые значения

Матрица доменного типа Dom::Matrix().