meijerGФункция Майера Г
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
meijerG([[a1, …, an], [an + 1, …, ap]],[[b1, …, bm], [bm + 1, …, bq]],z) meijerG([a1, …, an],[an + 1, …, ap],[b1, …, bm],[bm + 1, …, bq],z) meijerG(m,n,[a1, …, ap],[b1, …, bq],z)
meijerG( [[ a1, …, an], [ an + 1, …, ap]], [[ b1, …, bm], [ bm + 1, …, bq]] , z) представляет функцию Майера Г.
Следующие вызовы эквивалентны:
meijerG( [ a1, …, an], [ an + 1, …, ap], [ b1, …, bm], [ bm + 1, …, bq] , z), и
meijerG(m, n, [ a1, …, an, an + 1, …, ap], [ b1, …, bm, bm + 1, …, bq] , z).
meijerG( [[ a1, …, an], [ an + 1, …, ap]], [[ b1, …, bm], [ bm + 1, …, bq]] , z) представляет функцию Майера Г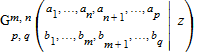
. Функция задана как
,
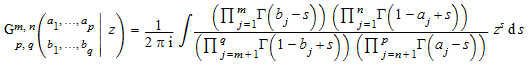где 0 ≤ m ≤ q и 0 ≤ n ≤ p. Параметры a i, b j и аргумент z могут быть комплексными числами. Интеграл представляет обратное Преобразование Лапласа или, более конкретно, тип Меллин-Барнса интеграла. Дополнительную информацию см. в разделе Algorithms.
Если m = 0, m = q, n = 0, n = p, p = 0, или q = 0, можно передать пустые списки параметров meijerG: [a 1, …, a n] = [], [a n + 1, …, a p] = [], [b 1, …, b m] = [], или [b m + 1, …, b q] = [].
Никакая пара параметров a i - b j, i = 1, …, n. j = 1, …, m, должен отличаться положительным целым числом. Таким образом никакой полюс
не совпадает ни с каким полюсом
. В противном случае, meijerG возвращает ошибку.
Функции Майера Г различными параметрами могут представлять ту же функцию:
Функция Майера Г симметрична относительно параметров. Изменение порядка в каждом из следующих списков параметров не изменяет получившуюся функцию Майера Г: [a 1, …, a n], [a n + 1, …, a p], [b 1, …, b m], [b m + 1, …, b q].
Если z не является отрицательным вещественным числом, функция удовлетворяет следующей идентичности
:.
Если 0 <n <p и r = a 1 - a p является целым числом, функция удовлетворяет следующей идентичности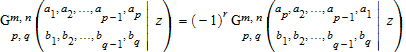
:.
Если 0 <m <q и r = b 1 - b q является целым числом, функция удовлетворяет следующей идентичности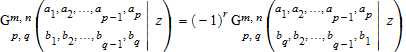
:.
Согласно этим правилам, meijerG вызов функции может возвратить meijerG модифицированными входными параметрами.
Если по крайней мере один из аргументов является числом с плавающей запятой, и все другие аргументы могут быть преобразованы в числа с плавающей запятой, функция возвращает значение с плавающей точкой.
Конкретный выбор параметров может уменьшать функцию Майера Г до более простых специальных или элементарных функций. Большинство специальных функций может быть выведено из функции Майера Г. Во многих случаях можно переписать результаты, включающие meijerG в терминах более элементарных функций с помощью simplify или Simplify. Смотрите пример 3.
Вызов meijerG([[], []], [[], []], x) возвращается 0.
Когда названо аргументами с плавающей точкой, эта функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Для точных или символьных аргументов, meijerG функция возвращает meijerG:
meijerG([[1],[]], [[],[2]],x)
meijerG([[1], [1/2]], [[], [1/2]], PI + I)
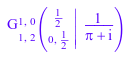
Для аргументов с плавающей точкой, meijerG возвращает значения с плавающей точкой:
meijerG([[1], []], [[1], [1/2]], 3.0), meijerG([[PI], [2]], [[], [3]], 4.0), meijerG([[I+1,2], []], [[1/(I+1), 1/2],[]], 0.5*I)
Функции diff и float обработайте выражения, включающие функцию Майера Г:
diff(meijerG([[a], [b]], [[c], [d]], x), x)
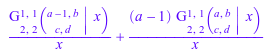
Дифференцируя функцию Майера Г относительно одного из ее параметров a 1, …, b q обычно не приводит к функциям Майера Г. Такие производные не реализованы:
diff(meijerG([a], [b], [c], [d], z), a)
Можно выполнить выражения, включающие meierG численно использующий float:
meijerG([[1], []], [[2], [sqrt(PI)]], 3) ~= float(meijerG([[1], []], [[2], [sqrt(PI)]], 3))
delete z:
Конкретный выбор параметров может уменьшать функцию Майера Г до более простых специальных или элементарных функций. Используйте simplify или Simplify получить такое представление:
simplify(meijerG([[], []], [[0], []], z))
simplify(meijerG([[1], []], [[1/2], [0]], z))
simplify(meijerG([[], []], [[1/2, -1/2], []], z))
Можно проверить эти отношения численно:
z:= float(PI+I): meijerG([[], []], [[0], []], z) = exp(-z);
meijerG([[1], []], [[1/2], [0]],z) = float(sqrt(PI)*erf(sqrt(z)))
meijerG([[], []], [[1/2, -1/2], []], z) = 2*besselK(1, 2*sqrt(z))
|
'Первый список параметров': арифметические выражения |
|
'Второй список параметров': арифметические выражения |
|
'Аргумент': арифметическое выражение |
|
Целые числа, удовлетворяющие 0 ≤ m ≤ q, 0 ≤ n ≤ p или символьные выражения. |
Арифметическое выражение.
z
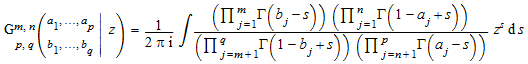
связал комплексный криволинейный интеграл с одним из следующих типов путей к интегрированию:
Контур идет от - i ∞ i ∞ так, чтобы все полюса
, j = 1, …, m, лгали праву пути и всем полюсам
, k = 1, …, n, лгали левым пути. Интеграл сходится если
, |arg (z) | <c π. Если |arg (z) | = c π, c ≥ 0, интеграл сходится абсолютно когда p = q и ℜ (ψ) <-1, где
. Когда p ≠ q, интеграл сходится, если вы выбираете контур так, чтобы контур указал близкий i ∞ и - i, ∞ имеют действительную часть удовлетворение σ
.
Контур является началом цикла и окончанием в infinity и окружением всех полюсов
, j = 1, …, m, перемещаясь в обратном направлении, но ни один из полюсов
, k = 1, …, n. Интеграл сходится если q ≥ 1 и или p <q или p = q и |z | <1.
Контур является началом цикла и окончанием в - ∞ и окружение всех полюсов
, k = 1, …, n, перемещающийся в положительное направление, но ни один из полюсов
, j = 1, …, m. Интеграл сходится если p ≥ 1 и любой p> q или p = q и |z |> 1.
Для данного набора параметров контур, выбранный в определении функции Майера Г, является тем, для которого сходится интеграл. Избегать беспорядка, если интеграл сходится для нескольких контуров, всего вывода контуров к той же функции.
Функция Майера Г удовлетворяет дифференциальному уравнению порядка max (p, q) относительно переменной z:
.
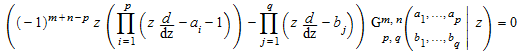Если p <q, это дифференциальное уравнение имеет регулярную сингулярность в z = 0 и неправильную сингулярность в z = ∞. Если p = q, точки, z = 0 и z = ∞ является регулярной сингулярностью, и существует дополнительная регулярная сингулярность в z = (-1) m + n - p.
Функция Майера Г представляет аналитическое продолжение Гипергеометрической функции (для получения дополнительной информации смотрите Люка в ссылках). Для конкретного выбора параметров можно выразить функцию Майера Г через гипергеометрическую функцию. Например, если никакие два из условий h b, h = 1, …, m, не отличаются целым числом или нулем, все полюса просты, и
,
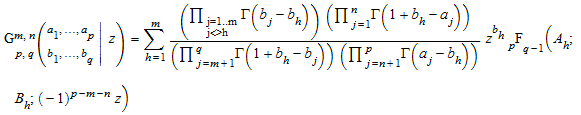где p <q или p = q и |z | <1. Символы A h, B h обозначает
и
.
И.Л. Люк, “Специальные функции и их приближения”, издание 1, Academic Press, Нью-Йорк, 1969.
А.П. Прудников, Ю. А. Брычков и О.И. Маричев, “Интегралы и ряд”, издание 3: более специальные функции, Гордон и нарушение, 1990.
М. Абрамовиц и И.А. Стегун, “Руководство Математических функций”, Дуврские Публикации, Нью-Йорк, 9-я печать, 1970.