Упростите выражение
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
simplify(f, <target>,options) simplify(L, <target>,options)
simplify(f) попытки упростить выражение f путем применения правил перезаписи термина.
simplify(f, target) ограничивает упрощение, чтобы назвать правила перезаписи применимыми к одной или нескольким целевым функциям.
cos, sinexp, ln, и sqrt цели были удалены. Используйте simplify вызовы функции без этих целей. В качестве альтернативы используйте radsimp вместо simplify с sqrt цель.
simplify функция выполняет последовательные упрощения. Это применяет определенный набор переписывающих термин правил к исходному выражению, переписывает выражение согласно этим правилам, берет результат и применяет следующий набор переписывающих термин правил. simplify функция принимает, что выход каждого правила “более прост”, чем вход без дальнейших проверок. Обычно этот метод быстрее, но менее надежен и управляем, чем алгоритм, используемый Simplify.
Если вы не задаете цель, simplify попытки упростить целое выражение. Этот первый шаг включает перезапись продуктов тригонометрических и экспоненциальных условий. После этого функция пытается упростить операнды выражения. Если выражение содержит специальные функции, вызовы MuPAD®, методы упрощения, доступные для этих функций.
Вызов simplify(L, target ) применяет упрощения в операндах объекта L.
Если вы задаете logic цель, simplify функция упрощает Булевы выражения. С logic цель, simplify не использует свойства и предположения, заданные для условий Булевых выражений.
Если вы задаете condition цель, simplify функция упрощает Булевы выражения. С condition цель, simplify свойства использования и предположения заданы для условий Булевых выражений.
simplify реагирует на свойства идентификаторов.
Используйте simplify функция, чтобы упростить следующие алгебраические выражения:
simplify(exp(x)-exp(x/2)^2)
![]()
f := ln(x) + ln(3) - ln(3*x) + (exp(x) - 1)/(exp(x/2) + 1): simplify(f)
![]()
Чтобы упростить Булевы выражения, используйте logic цель:
simplify((a and b) or (a and (not b)), logic)
![]()
В качестве альтернативы, чтобы упростить Булевы выражения, используйте condition цель. С condition цель, simplify использует свойства и предположения, заданные для условий Булевых выражений. С logic цель, simplify игнорирует те свойства и предположения:
simplify(x > x, condition), simplify(x > x, logic)
![]()
Опция IgnoreAnalyticConstraints позволяет вам получать более простые результаты с помощью набора чисто алгебраических упрощений:
simplify(ln(x^2 + 2*x + 1) - ln(x + 1))
![]()
simplify(ln(x^2 + 2*x + 1) - ln(x + 1), IgnoreAnalyticConstraints)
![]()
Если вы будете использовать эту опцию, simplifier не гарантирует равенства начального выражения и результата для всех символьных параметров.
Чтобы изменить количество шагов упрощения, используйте Steps опция:
f := ((exp(-x*I)*I)/2 - (exp(x*I)*I)/2)/(exp(-x*I)/2 + exp(x*I)/2): simplify(f); simplify(f, Steps = 10); simplify(f, Steps = 50)

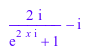
![]()
Ваши пользовательские функции могут иметь атрибуты упрощения. Например, предположите, что вы знаете, что f является аддитивной функцией, но вы не знаете больше о f. Поэтому вы не можете вычислить значение функции ни в какой точке кроме нуля, но можно использовать аддитивность:
f := funcenv( x -> if iszero(x) then 0 else procname(x) end):
f::simplify := proc(F)
local argument;
begin
argument := op(F,1);
if type(argument) = "_plus" then
map(argument, f)
else
F
end
end:f(x + 3*y) - f(3*y) = simplify(f(x + 3*y) - f(3*y))
![]()
Можно совершенствовать атрибут упрощения f далее. Например, можно указать, что это должно повернуть f(3*y) в 3*f(y). Противоположное правило (переписывающий f (x) + f (y) как f (x + y)) не контекстно-свободно. Поэтому вы не можете реализовать противоположное правило в атрибуте упрощения.
| |
|
Контейнерный объект: массив, hfarray, список, матрица, полином, набор или таблица. |
|
Один из идентификаторов |
|
При использовании этой опции simplifier применяет следующие правила к выражениям:
Используя |
|
Предел время допускал внутренний процесс упрощения. Значение обозначает максимальное время в секундах. По умолчанию время упрощения неограниченно. |
|
Отключите алгебраическое упрощение после конкретного количества шагов упрощения. Значение должно быть положительным целым числом. количеством по умолчанию шагов упрощения является |
Объект того же типа как входной объект f или L, соответственно.
fL