Упростите выражение
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Simplify(f) Simplify(f,Steps = numberOfSteps) Simplify(f,options)
Simplify(f) применяет переписывающие термин правила к f и возвращает самое простое выражение, которое это может найти.
Методы поиска самого простого представления выражения отличаются для Simplify и simplify. simplify функция выполняет линейный поиск, пытающийся улучшить результат, возвращенный предыдущим шагом упрощения. Simplify функционируйте использует результаты, возвращенные всеми предыдущими шагами упрощения (поиск по первому наилучшему совпадению). simplify функция быстрее. Simplify функция является медленнее, но более эффективной и более конфигурируемой.
Термин “самый простой” определяется следующим образом. Один объект более прост, чем другой, если он имеет меньшую оценку. Если два объекта имеют ту же оценку, Simplify выбирает более простой объект с помощью внутренней эвристики. Оценка является функцией, которая присваивает неотрицательный вещественный номер каждому объекту MuPAD®. Заменять оценку по умолчанию, используемую Simplify, используйте Valuation опция. Simplify использует оценку в поиске по первому наилучшему совпадению что касается определения лучшего результата в последнем шаге. Однако можно задать отдельный метод для итогового шага упрощения при помощи Criterion опция.
Процесс упрощения состоит из шагов. На каждом шаге, Simplify выполняет один из следующих видов задач для a := f или некоторые (ранее полученный) объект a эквивалентный f. На каждом шаге, Simplify может произвести новые объекты, эквивалентные f (результаты) или новые задачи сделать или оба:
'InitialStep' : Найдите все правила для a. Simplify функция выполняет поиск всех правил для каждого нового объекта a. Этот поиск не приводит ни к какому новому результату.
Перезапись шага: Примените одно правило к a. Этот шаг может или привести к сбою или произвести эквивалентный объект как результат.
Шаг подвыражения: Выполните один шаг в упрощении операнда a. Замените операнд на возвращенный результат (если существуют какие-либо результаты). Этот шаг может произвести новый эквивалентный объект.
Каждая открытая задача имеет приоритет, который определяет, что сделать затем. Упрощение завершает работу в любом из следующих случаев:
Нет никаких более открытых задач.
Simplify достигнутый ограничение по времени задано Seconds.
Simplify выполняемый максимальное количество шагов упрощения задано Steps.
Simplify возвращенный объект задан Goal.
Simplify всегда возвращает “самый простой” эквивалентный объект, найденный на всех шагах упрощения, если вы не задаете другой OutputType.
Правила формируют конкретный доменный Rule. Они состоят из шаблона (левая сторона), выражение (правая сторона) и опции.
MuPAD организует правила для Simplify в основах правила. Можно изменить основу правила по умолчанию при помощи RuleBase опция. Также можно задать собственный механизм выбора правила при помощи SelectRules опция.
Как правило, Simplify применяет выбранные правила к данному объекту a в целом. Следующий случай является исключением из этого правила. Если шаблон правила и объекта a оба сумма или продукт, затем Simplify применяет правило к каждой подсумме или промежуточному результату a это имеет то же количество операндов как шаблон.
При помощи ApplyRule опция, можно задать собственную функцию, которая применяет конкретное правило к конкретному объекту. В противном случае, Simplify использует метод по умолчанию.
Приложение правила к объекту a сбои, если шаблон не соответствует (см. match) объект a. Производительность Simplify строго зависит от количества успешных соответствий. Поэтому, если вы задаете свою собственную основу правила, она должна избавиться от несоответствия с правилами перед выбором правила.
Шаг упрощения для операнда работает как шаг упрощения над упрощением f. Исключения следующие. Выполняя шаг упрощения для операнда, MuPAD не применяет определенные правила (см. детали о SelectRules).
MuPAD определяет приоритеты открытых задач можно следующим образом. Приоритет выполнения начального шага для выражения зависит от оценки выражения. Приоритет выполнения шага упрощения на операнде зависит от отношения между полной оценкой выражения и оценкой операнда и приоритетом задачи самого высокого ранга в списке ожидающих выполнения задач операнда. Наконец, приоритет применения правила к выражению равняется приоритету правила, умноженного на оценку выражения.
Стратегия определяет приоритет правила. Смотрите Strategy опция для деталей.
Simplify никогда не использует симметрию математической эквивалентности выражений. Поэтому можно использовать Simplify как общая система перезаписи.
Simplify карты к спискам, наборам и таблицам.
Для доменных элементов dупрощение может быть перегружен двумя способами. Во-первых, Simplify использует паз d::dom::Simplify. Если тот паз не существует, Simplify использование d::dom::simplify. Если паз, что Simplify использование не является списком, Simplify вызывает паз и принимает результат как простой (даже если оценка не соглашается). В этом случае, Simplify не применяет никакие другие правила к d. Однако Simplify использует оценку, чтобы решить, должна ли она заменить доменный элемент, который происходит как операнд в другом объекте с его “упрощенной” версией. Если паз является списком, его записи должны быть правилами и Simplify применяет их согласно их приоритету.
Самый легкий способ использовать Simplify должен принять все значения по умолчанию, и затем включить выражение, которое вы хотите упростить:
Simplify(sin(x)^2 + cos(x)^2)
![]()
По умолчанию, Simplify возвращает только одно выражение, которое функция рассматривает как самое простое. Чтобы возвратить список всех эквивалентных выражений, используйте All опция:
Simplify(sin(x)^2 + cos(x)^2, All)
![]()
Выход предыдущего примера короток потому что, как только simplifier находит 1, это сразу останавливается. После этого simplifier не ищет другие эквивалентные выражения. Кроме того, simplifier отбрасывает эквивалентные выражения, которые значительно более сложны, чем лучшее выражение, найденное ранее. Можно выключить оба механизма:
Simplify(sin(x)^2 + cos(x)^2, All, Discard = FALSE,
IsSimple = FALSE)
По умолчанию, Simplify использует оценку, которая способствует выражениям с меньшим количеством различных иррациональных подвыражений. Например, Simplify принимает что выражение, содержащее только sin(x) или cos(x) более просто, чем выражение, содержащее обоих:
Simplify(cos(x)*sin(x))
![]()
Если вы берете length как мера по сложности для выражений, Simplify возвращает другой результат:
Simplify(cos(x)*sin(x), Valuation = length)
![]()
Количество по умолчанию шагов равняется 100. Чтобы изменить максимальное количество возможных шагов упрощения, используйте Steps опция. Например, уменьшение (приводящий к ускорению) и увеличение (приводящий к, вероятно, лучшему упрощению) количество шагов упрощения:
f := ln(x) + ln(3) - ln(3*x) + (exp(x) - 1)/(exp(x/2) + 1): Simplify(f, Steps = 8), Simplify(f, Steps = 120)
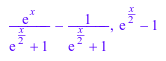
delete f:
Для многих выражений количество по умолчанию шагов упрощения не позволяет simplifier находить хорошее упрощение:
Simplify(e^(a* x *(a + 1) + b2* y *(y + b2* x* y)))
![]()
Увеличение этого предела часто помогает:
Simplify(e^(a* x *(a + 1) + b2* y *(y + b2* x* y)), Steps=125)
![]()
По умолчанию функции упрощения не комбинируют логарифмы:
Simplify(ln(x^3 - 1) - ln(x - 1))
![]()
Используя IgnoreAnalyticConstraints опция, часто можно получать более короткие результаты:
Simplify(ln(x^3 - 1) - ln(x - 1), IgnoreAnalyticConstraints)
![]()
Можно написать то же выражение в различных системах координат. Например, используйте Декартовы и полярные координаты:
assume(x/r = cos(Symbol::theta)): assumeAlso(y/r = sin(Symbol::theta)): assumeAlso(r = sqrt(x^2+y^2)): x/sqrt(x^2+y^2) + I*y/sqrt(x^2+y^2) = exp(I*Symbol::theta); Simplify(%)
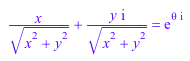
![]()
Следующее выражение эквивалентно exp(x):
a := -1/(sin(1/2*I*x)^2 + 4*sin(1/4*I*x)^4 -
4*sin(1/4*I*x)^2 + 1)*(sin(1/2*I*x)^2 -
4*I*sin(1/2*I*x)*sin(1/4*I*x)^2 + 2*I*sin(1/2*I*x) -
4*sin(1/4*I*x)^4 + 4*sin(1/4*I*x)^2 - 1)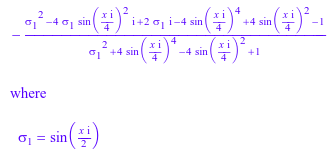
Simplify распознает эквивалентность a и exp(x) в 100 шагах. Чтобы показать, как функция доказывает эквивалентность на каждом шаге, используйте OutputType опция. Обратите внимание на то, что доказательство, возвращенное Simplify не доказательство в строгом математическом смысле. Simplify использует правила от основы правила по умолчанию:
Simplify(a, OutputType = "Proof")
Input was -(sin((x*I)/2)^2 - 4*sin((x*I)/2)*sin((x*I)/4)^2*I + 2*sin((x*I)/2)*I - \ 4*sin((x*I)/4)^4 + 4*sin((x*I)/4)^2 - 1)/(sin((x*I)/2)^2 + 4*sin((x*I)/4)^\ 4 - 4*sin((x*I)/4)^2 + 1) Applying the rule Simplify::combineSinCos gives cos(x*I) - sin(x*I)*I Applying the rule Simplify::expand gives cosh(x) + sinh(x) Applying the rule X -> rewrite(X, exp) gives exp(x) END OF PROOF
Также можно использовать Simplify для экспериментов с формальными грамматиками, данными только несколькими правилами. В этом случае лучший подход не должен использовать основы правила, но использовать SelectRules метод, который возвращает список всех правил. Следующий пример представляет общий ассоциативный оператор ?. Пример вычисляет количество всех возможных размещений круглых скобок. Во-первых, задайте operator, и затем присоедините его к функции, которая управляет ее выходом (см. funcenv). Укажите, что единственное применимое правило является ассоциативным законом. В вызове Simplify, определите номер шагов к очень большому значению, чтобы выполнить полный поиск. Обратите внимание на то, что большинство грамматик производит бесконечно много слов и проводит бесконечное время, чтобы закончить полный поиск:
_f := funcenv(() -> procname(args())):
operator("?", _f, Binary, 1000):
R := Rule((X ? Y) ? Z, X ? (Y ? Z)):
selectProc := () -> [R]:
S := Simplify(u ? v ? x ? y ? z, Steps = 10^10,
SelectRules = selectProc, All):PRETTYPRINT := FALSE: print(Plain, S): PRETTYPRINT := TRUE:
[u ? (v ? (x ? (y ? z))), u ? (v ? ((x ? y) ? z)), u ? ((v ? (x ? y)) ? z)\ , u ? (((v ? x) ? y) ? z), u ? ((v ? x) ? (y ? z)), (u ? (v ? x)) ? (y ? z\ ), ((u ? v) ? x) ? (y ? z), (u ? v) ? (x ? (y ? z)), (u ? v) ? ((x ? y) ? \ z), (u ? (v ? (x ? y))) ? z, (u ? ((v ? x) ? y)) ? z, ((u ? (v ? x)) ? y) \ ? z, (((u ? v) ? x) ? y) ? z, ((u ? v) ? (x ? y)) ? z]
Существует 14 возможных способов поместить круглые скобки:
nops(S);
delete fout, _f, R, S, selectProc:
operator("?", Delete):![]()
Если вы хотите задать больший ряд правил, лучший подход должен использовать вашу собственную основу правила. Классическим примером является дифференцирование. Несмотря на то, что эвристический поиск должен быть медленнее, чем простой рекурсивный алгоритм, этот пример подходит для демонстрации некоторых факторов КПД. Запустите путем определения функциональной среды mydiff это ничего не делает:
mydiff := funcenv(mydiff): mydiff::type := "mydiff"
![]()
Цель этого определения состоит в том, чтобы показать, что виды MuPAD управляют в основах правила типами выражений, к которым MuPAD применяет те правила. Поэтому mydiff получает его собственный тип. Теперь задайте основу правила Myrules с обычными правилами дифференцирования. Не используйте дополнительные правила:
Myrules := newDomain("Myrules"):
Myrules::mydiff :=
[Rule(mydiff(f, x), 0, {(f, x) -> not has(f, x)}),
Rule(mydiff(x, x), 1),
Rule(mydiff(x^n, x), n*x^(n - 1)),
Rule(mydiff(f*g, x), f*mydiff(g, x) + g*mydiff(f, x)),
Rule(mydiff(f + g, x), mydiff(f, x) + mydiff(g, x))
]:Эта основа правила работает на выражение x 2:
Simplify(mydiff(x^2, x), RuleBase = Myrules)
![]()
Однако основа правила не работает на следующее выражение:
Simplify(mydiff(x + 3, x), RuleBase = Myrules)
![]()
Попытайтесь улучшить ту основу правила. Как первый шаг, увеличьте число шагов упрощения. Увеличение числа шагов не помогает в этом случае:
Simplify(mydiff(x + 3, x), RuleBase = Myrules, Steps = 200)
![]()
Как второй шаг, более тщательно изучите по эквивалентным выражениям, возвращенным Simplify. Иногда, Simplify находит ожидаемый результат, но не возвращает его, потому что оценка ожидаемого результата выше, чем оценка некоторого другого эквивалентного выражения. Для выражения x + 3, Simplify функция не находит ожидаемый результат:
l := Simplify(mydiff(x + 3, x), RuleBase = Myrules, All)

Обратите внимание на то, что производная 1 появляется в результате. Используйте OutputType опция, чтобы проверять, как Simplify управляет третьим сроком l[3] и как это доказывает эквивалентность ввода и вывода на каждом шаге:
Simplify(mydiff(x + 3, x), RuleBase = Myrules,
Goal = l[3],
OutputType = "Proof")Input was mydiff(x + 3, x) Applying the rule mydiff(f*g, x) -> f*mydiff(g, x) + g*mydiff(f, x) gives (x + 3)*mydiff(1, x) + mydiff(x + 3, x) END OF PROOF
Теперь вы видите, что для каждого выражения f, необходимо задать правило для diffentiating продуктов потому что f = 1 f. Измените то правило:
(Myrules::mydiff)[4] := Rule(mydiff(f*g, x),
f*mydiff(g, x) + g*mydiff(f, x),
{(f, g) -> f <> 1 and g <> 1}):Обновленная основа правила работает:
Simplify(mydiff(x + 3, x), RuleBase=Myrules, Remember=FALSE)
![]()
Используйте несколько опций, чтобы оптимизировать вызов Simplify. Как первый шаг, измерьтесь, сколько шагов типичный пример делает прежде, чем возвратить ожидаемый выходной параметр:
Simplify(mydiff(5*x^4 + x^3 + x^2 + x + 1, x),
RuleBase = Myrules,
Steps = 2000,
Goal = 20*x^3 + 3*x^2 + 2*x + 1,
OutputType = "NumberOfSteps")![]()
Избегайте приложения равенства f = f + 0. Выключите помнить механизм. Когда помнить механизм работает, Simplify игнорирует изменения в основе правила:
Myrules::mydiff[5] := Rule(mydiff(f + g, x),
mydiff(f, x) + mydiff(g, x),
{(f, g) -> f <> 0 and g <> 0}):
Simplify(mydiff(5*x^4 + x^3 + x^2 + x + 1, x),
RuleBase = Myrules,
Steps = 2000,
Goal = 20*x^3 + 3*x^2 + 2*x + 1,
OutputType = "NumberOfSteps",
Remember = FALSE)![]()
Затем попытайтесь изменить критерии оценки. Например, используйте length:
Simplify(mydiff(5*x^4 + x^3 + x^2 + x + 1, x),
RuleBase = Myrules,
Steps = 2000,
Goal = 20*x^3 + 3*x^2 + 2*x + 1,
OutputType = "NumberOfSteps",
Valuation = length)![]()
Оптимизировать вызов Simplify, также можно задать собственную стратегию упрощения. Например, первое правило, кажется, обеспечивает очень полезное упрощение каждый раз, когда оно применяется. Поэтому присвойте высокий приоритет этому правилу путем предположения, что в среднем это правило упрощает свой вход до 0.03 из исходной сложности:
Myrules::mydiff[1] := subsop(Myrules::mydiff[1],
4 = table("MyStrategy" = 0.03)):
Simplify(mydiff(5*x^4 + x^3 + x^2 + x + 1, x),
RuleBase = Myrules,
Steps = 3000,
Goal = 20*x^3 + 3*x^2 + 2*x + 1,
OutputType = "NumberOfSteps",
Strategy = "MyStrategy")![]()
При использовании оценки length, вы получаете следующий результат:
Simplify(mydiff(5*x^4 + x^3 + x^2 + x + 1, x),
RuleBase = Myrules,
Steps = 3000,
Goal = 20*x^3 + 3*x^2 + 2*x + 1,
OutputType = "NumberOfSteps",
Strategy = "MyStrategy",
Valuation = length)![]()
Когда вы используете находящееся в matcher упрощение, большинство правил не соответствует к большинству объектов. Попытка совпадать со всеми правилами ко всем объектам производит много шагов перезаписи сбоя. Рекомендуемый подход должен отбросить эти провальные правила во время начального шага. Отбрасывание провальных правил сокращает число шагов. Это также увеличивает время выполнения на шаг небольшим количеством. Определение процедуры вместо списка правил может помочь вам отбросить провальные правила во время начального шага. Можно задать правила при помощи шаблона или процедуру в качестве их первого аргумента:
Myrules::mydiff :=
proc(df)
begin
[if not has(op(df, 1), op(df, 2)) then
Rule(X -> 0)
else
case type(op(df, 1))
of "_plus" do
Rule(X -> map(op(X, 1), mydiff, op(X, 2)));
break
of "_mult" do
Rule(mydiff(f*g, x), f*mydiff(g, x) + g*mydiff(f, x));
break
of "_power" do
Rule(X -> op(X, [1,2])*op(X, [1,1])^(op(X, [1,2]) - 1));
break
of DOM_IDENT do
assert(op(df, 1) = op(df, 2));
Rule(X -> 1);
break
otherwise
null()
end_case
end_if]
end_proc:
Simplify(mydiff(5*x^4 + x^3 + x^2 + x + 1, x),
RuleBase = Myrules,
Steps = 200,
Goal = 20*x^3 + 3*x^2 + 2*x + 1,
OutputType = "NumberOfSteps")![]()
delete Myrules, mydiff:
|
Любой объект |
|
Когда вы используете |
|
Опция, заданная как Задайте функциональный |
|
Опция, заданная как Задайте функциональный |
|
Опция, заданная как Задайте функциональный |
|
Опция, заданная как Если |
|
При использовании этой опции simplifier применяет следующие правила к выражениям:
При использовании этой опции, |
|
Опция, заданная как Задайте функциональный |
|
Опция, заданная как Ограничьте усилие, которое инвестируют в один шаг упрощения. Здесь |
|
Опция, заданная как Задайте тип возвращаемого значения. Значение Даже если вы указываете, что выход вводит как Если вы устанавливаете эту опцию на Технически, доказательствами являются объекты того же типа как выход |
|
Опция, заданная как
|
|
Опция, заданная как Основа правила |
|
Опция, заданная как Когда вы используете |
|
Опция, заданная как Когда вы используете Можно задать любую основу правила и использовать любой вид правила. Единственным ограничением является тот |
|
Опция, заданная как Когда вы используете |
|
Опция, заданная как Когда вы используете |
|
Опция, заданная как Когда вы используете По умолчанию, Если конкретное правило не распознает стратегию Если вы используете Если |
|
Опция, заданная как Когда вы используете Хорошая оценка является компромиссом между концепциями максимального типа и контекстно-свободным. Для контекстно-свободной оценки и оператор выражения и оценки операндов определяют оценку выражения. Для оценки максимального типа обычно оценка выражения равняется максимуму оценок его операндов. Типичным контекстно-свободным примером является MuPAD предлагает контекстно-свободной оценке |
Simplify возвращает объект, математически эквивалентный входу. С опцией OutputType = "All", Simplify функция возвращает список всех эквивалентных объектов, найденных во время упрощения. С опцией OutputType = "NumberOfSteps", функция возвращает положительное целое число. С опцией OutputType = "Proof", функция возвращает строку, содержащую доказательство эквивалентности входа и результата.
f