numeric::product
Числовое приближение продуктов
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Синтаксис
numeric::product(f,i = a .. b) numeric::product(f,i in RootOf(p, <x>)) numeric::product(f,i = RootOf(p, <x>)) numeric::product(f,i in {x1, x2, …}) numeric::product(f,i = {x1, x2, …})
Описание
numeric::product(f, i = a..b) вычисляет числовое приближение
.
numeric::product (f, i = RootOf(p,x)) вычисляет числовое приближение продукта f по корням полиномиального p.
numeric::product(f, i in { x1, x2, …}) вычисляет числовое приближение
.
Вызов numeric::product(...) эквивалентно вызову float атрибут product через float ( hold( product )(...)), float ( freeze( product )(...)) или product::float(...).
Если существуют другие символьные параметры в f, кроме переменной i, символьного вызова numeric::product возвращен. Числовые выражения такой как
,
и т.д. приняты и преобразованы в числа с плавающей запятой.
Примечание
Для конечных продуктов, numeric::product только возвращает _mult ( float(f) $ i=a..b). См. пример 3.
Вызов numeric::product(f, i = { x1, x2, …}) вычисляет числовые приближения x[1]x2 и т.д. замены эти значения в f (i) и умножают результаты.
Вызовы numeric::product(f, i in { x1, x2, …}) и numeric::product(f, i = { x1, x2, …}) эквивалентны.
Вызов numeric::product (f, i in RootOf(p, x)) вычисляет числовые приближения всех корней p, заменяет этими значениями в f (i) и умножает результаты. См. Пример 2.
Вызовы numeric::product(f, i in RootOf(p, x)) и numeric::product(f, i = RootOf(p, x)) эквивалентны.
Взаимодействия среды
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность и влияет на максимальное количество шагов, используемых в расчете.
Примеры
Пример 1
Мы демонстрируем некоторые эквивалентные призывы к числовым продуктам:
numeric::product(1+1/k^2, k = 1..infinity), float(hold(product)(1+1/k^2, k = 1..infinity)), float(freeze(product)(1+1/k^2, k = 1..infinity)), product::float(1+1/k^2, k = 1..infinity);
product сбои, чтобы найти закрытую форму для следующего продукта:
product(1 - 1/4^k, k = 1..infinity);
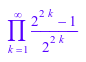
float неявно использование numeric::product вычислить числовое приближение:
float(%);
Точное значение следующего бесконечного произведения
:
numeric::product(exp((-1)^(k+1)*k^(-1/2)), k = 1..infinity) = float(exp((1-sqrt(2))*zeta(1/2)))
Пример 2
Мы вычисляем приближение продукта по корням полинома:
numeric::product(sin(r), r = RootOf(x^2 - PI^2/4, x))
Если многочленное выражение содержит дополнительный indeterminates, символьный вызов numeric::product возвращен:
numeric::product(r+PI, r = RootOf(x^8 + c*x - PI^2/4, x))
Пример 3
numeric::product может также быть использован для расчета конечные продукты:
numeric::product(1-1/k^2, k = 2..10^n) $ n in { 2, 3, 4 }
Однако начиная с numeric::product использование _mult внутренне так или иначе более эффективно вызвать _mult непосредственно:
_mult(float(1-1/k^2) $ k = 2..10^n) $ n in { 2, 3, 4 }
Пример 4
Следующий продукт возвращен символически, потому что он содержит дополнительный неопределенный k:
numeric::product(1-1/n^k, n = 2..infinity)
Параметры
|
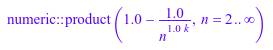
Арифметическое выражение в зависимости от |
|
Список продукции: идентификатор или индексированный indentifier |
|
целые числа или |
|
Одномерное многочленное выражение в |
|
Неопределенный |
|
Возвращаемые значения
число с плавающей запятой или символьное выражение типа numeric::product.
Алгоритмы
Бесконечные произведения вычисляются путем подведения итогов ряда
через numeric::sum.
numeric::product использование numeric::polyroots вычислить числовые приближения к корням полиномы.