numlib::contfracОбласть непрерывных дробей
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
numlib::contfrac(x, <n>)
numlib::contfrac(x) создает приближение непрерывной дроби для вещественного числа x.
Если x целое число или рациональное число и n не задан, непрерывная дробь возвращена, который представляет x точно. См. Пример 1.
Иррациональные численные значения x такой как 1 + sqrt(2) или PI/3 сначала преобразованы в числа с плавающей запятой. Первый n учтены значительные десятичные числа чисел с плавающей запятой. Если n не задан, n = DIGITS используется. Значение непрерывной дроби (данный numlib::contfrac ::rational) удовлетворяет
![]() .
.
Целые числа или рациональные числа также преобразованы в числа с плавающей точкой, если точность n задан.
Объекты типа numlib::contfrac может быть обработан обычными арифметическими операциями. Они чувствительны к переменной окружения DIGITS если числа с плавающей запятой или иррациональные численные значения включены.
Используйте contfrac вычислить приближения непрерывной дроби выражений, включающих символьные параметры.
Для рациональных чисел возвращены точные представления:
numlib::contfrac(123/1234)
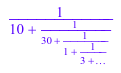
Рациональное представление (второй операнд непрерывной дроби) совпадает с рациональным оригиналом:
numlib::contfrac::rational(%), expr(%), op(%, 2)
![]()
Ограниченные приближения непрерывной дроби могут быть вычислены путем передачи точности в качестве второго аргумента:
numlib::contfrac(123/1234, 2), numlib::contfrac(123/1234, 3), numlib::contfrac(123/1234, 5)
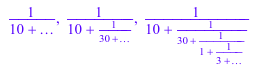
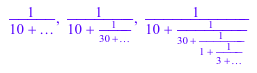
Коэффициенты извлечены методом nthcoeff:
cf := numlib::contfrac(12/123)
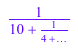
nthcoeff(cf, 1), nthcoeff(cf, 2), nthcoeff(cf, 3), nthcoeff(cf, 4)
![]()
Внутренний список коэффициентов может также быть запрошен через op:
op(cf, 1)
![]()
delete cf:
numlib::contfrac может также вычислить приближения непрерывной дроби иррациональных чисел:
numlib::contfrac(PI, 2), numlib::contfrac(PI, 4), numlib::contfrac(PI, 5)
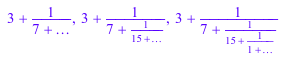
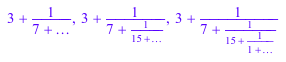
Конечное приближение непрерывной дроби может рассматриваться как интервал чисел (символ, … представляет номер между 0 и 1):
numlib::contfrac::rationalInterval(numlib::contfrac(PI, 2));
![]()
float(%)
![]()
Все основные арифметические операции доступны для непрерывных дробей:
x := numlib::contfrac(PI, 3): y := numlib::contfrac(1/12): DIGITS:= 3: 3/x + sqrt(2)*y^(1/3)
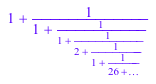
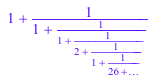
delete x, y, DIGITS:
Мы ищем простую непрерывную дробь в интервале:
numlib::contfrac::convert(1/2 - 1/10^8, 1/2 + 1/10^8)
![]()
![]()
numlib::contfrac::convert(PI, PI + 1/10^10)
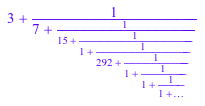
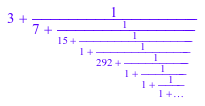
|
Действительное числовое выражение |
|
Количество значительных цифр: положительный целочисленный больший |