contfracОбласть непрерывных дробей
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
contfrac(r, <n>) contfrac(f,x, <m>) contfrac(f,x = x0, <m>)
contfrac(r) создает приближение непрерывной дроби вещественного числа r.
contfrac(f, x = x0) создает приближение непрерывной дроби выражения f как функция x вокруг x = x0.
Расширение непрерывной дроби contfrac(r n ) из вещественного или числового выражения r расширение формы
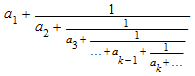
где a1 целочисленный floor(r) и a2, a3... положительные целые числа.
Непрерывная дробь вычисляется numlib::contfrac(r < n >); расширение возвращено contfrac имеет доменный тип numlib::contfrac.
См. документацию numlib::contfrac для получения дальнейшей информации.
Расширение непрерывной дроби contfrac(f, x = x0) из символьного выражения f в неопределенном x расширение формы
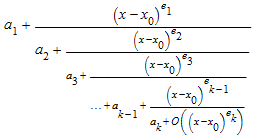
где
a 1, …, a k является арифметическими выражениями, не содержащими степени x - x 0. Коэффициенты a 2, …, a k являются ненулевыми.
e 1 является рациональным числом и e 2, …, e, k является положительными рациональными числами. Если a 1 ≠ 0, то e 1 положителен также.
Если![]() или
или x0 = complexInfinity, условия (x - x 0) e i должны быть заменены![]() .
.
Для символьных выражений f, contfrac(f, x = x0) возвращает расширение доменного типа contfrac.
Можно также вызвать contfrac(f) не задавая идентификатор x. В этом случае, contfrac извлекает indeterminates в f автоматически через indets. FAIL возвращен, если больше чем один неопределенный найден.
Если m не задан, значение по умолчанию m = ORDER используется.
contfrac использует функциональный Series::Puiseux::contfrac вычислить непрерывную дробь в символьном случае. Если f рациональная функция относительно переменной x расширения, и 'усечение order' m не задан, затем contfrac возвращает точное расширение непрерывной дроби f. См. пример 3.
Когда названо иррациональным численным значением r, функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность. Для символьных выражений f, функция чувствительна к переменной окружения ORDER который определяет количество условий в усеченных последовательных расширениях.
Мы вычисляем некоторые расширения непрерывной дроби вещественных чисел:
contfrac(27/31), contfrac(PI, 5)
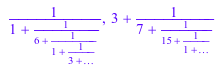
Они могут также быть вычислены прямыми вызовами numlib::contfrac:
numlib::contfrac(27/31), numlib::contfrac(PI, 5)
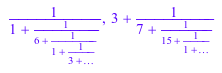
Мы вычисляем символьные непрерывные дроби функций:
contfrac(exp(x), x = 0), contfrac(exp(-3*x^2), x = 0)
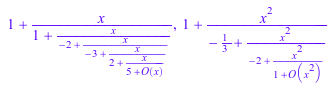
Если никакая переменная расширения не задана, символьное выражение, которое будет расширено, должно быть одномерным:
contfrac(exp(x*y))
Error: First argument must be a univariate expression. [contfrac::function]
Символьные параметры приняты, если переменная расширения задана:
contfrac(exp(x*y), x)
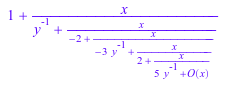
В следующем вызове мы указываем, что расширение указывает x = 1 и запросите определенное 'количество условий' третьим аргументом:
contfrac(exp(x*y), x = 1, 3);
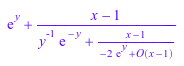
Для рациональных функций возвращены точные представления, когда никакое определенное 'количество условий' не требуют. Метод "rational" возвращает рациональное выражение, эквивалентное непрерывной дроби:
cf := contfrac((x - y)/(x^3 + y^3), x, 2): cf, contfrac::rational(cf);
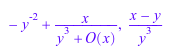
cf := contfrac((x - y)/(x^3 + y^3), x): cf, contfrac::rational(cf);
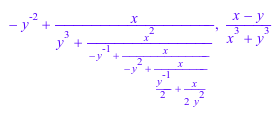
К коэффициентам и условиям расширения непрерывной дроби могут получить доступ функции nthcoeff и nthterm:
cf := contfrac(sin(1/x), x = infinity, 4)
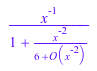
nthcoeff(cf, 1), nthcoeff(cf, 2), nthcoeff(cf, 3), nthcoeff(cf, 4);
![]()
nthterm(cf, 1), nthterm(cf, 2), nthterm(cf, 3)
![]()
delete cf:
Мы можем вычислить последовательное расширение непрерывной дроби через series:
cf := contfrac(sin(x)/(x - PI) - 1, x = PI)
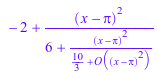
Если никакие дальнейшие аргументы не даны в series, переменной расширения по умолчанию является op(cf, 3); точкой расширения по умолчанию является op(cf, 4):
op(cf, 3), op(cf, 4)
![]()
series(cf)
![]()
Оба серийная переменная, а также точка расширения могут быть переданы явным образом series.
series(cf, x = PI)
![]()
Однако значения должны совпасть со значениями, использовался для расчета непрерывной дроби: В следующем вызове, точка расширения по умолчанию x = 0 используется series. Это сталкивается с точкой расширения x = PI из непрерывной дроби:
series(cf, x)
Error: Expansion point 'PI' of the continued fraction does not coincide with the requested expansion point '0' of the series. [contfrac::series]
delete cf:
|
Вещественное число или числовое выражение, которое может быть преобразовано в действительное число с плавающей запятой |
|
Количество значительных десятичных цифр: положительное целое число. Значением по умолчанию является |
|
Арифметическое выражение, интерпретированное как функция x |
|
Идентификатор |
|
Точка расширения: арифметическое выражение |
|
'Количество условий': положительное целое число. Значением по умолчанию является |
Вызовите contfrac(r n ) с численным значением r возвращает объект типа numlib::contfrac. Вызов contfrac(f, x = x0 m ) с символьным выражением f возвращает объект типа contfrac. FAIL возвращен если никакое последовательное расширение f вокруг x0 мог быть вычислен.