ode::seriesСерийные решения обыкновенного дифференциального уравнения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
ode::series(Ly, y(x),x | x = x0, <order>) ode::series({Ly, <inits>}, y(x),x | x = x0, <order>)
ode::series(Ly, y(x), x = x0) вычисляет первые сроки последовательных расширений решений Ly относительно переменной x вокруг точки x0.
ode::series попытки вычислить или Ряд Тейлора, Ряд Лорана или серию Пюизе решений дифференциального уравнения Ly вокруг точки x=x0.
Предположим тот Ly нелинейное дифференциальное уравнение. Если x0 обычная точка Ly затем Ряд Тейлора вычисляется в противном случае выражение типа "series" возвращен. Если начальные условия даны в точке x0 затем ответ выражается в терминах функционального y(x) и его производные оценили в точке x0. Смотрите пример 1.
Предположим тот Ly линейное дифференциальное уравнение. Если x0 обычная точка Ly затем Ряд Тейлора вычисляется, если Ly является, кроме того, гомогенным и x0 регулярная точка затем, ряд Пюизе вычисляется (содержащий возможные логарифмические условия), в противном случае выражение типа "series" возвращен. Если начальные условия даны в точке x0 затем ответ или выражается в терминах функционального y(x) и его производные оценили в точке x0 или это может быть выражено в терминах произвольных постоянных.
Рассмотрите следующее нелинейное дифференциальное уравнение:
Ly := x^2*diff(y(x),x)+y(x)-x
![]()
Мы вычисляем серийные решения в точке 0, которая является особой точкой:
ode::series(Ly, y(x), x=0)
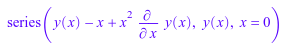
Затем мы вычисляем серийные решения в регулярной точке 1:
ode::series(Ly, y(x), x=1)
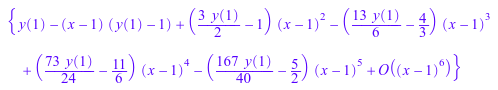
И мы можем также поместить некоторые начальные условия в точку 1:
ode::series({y(1)=1, Ly}, y(x), x=1)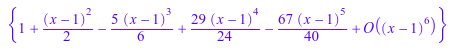
Рассмотрите следующее линейное дифференциальное уравнение:
Ly := (2*x+x^3)*diff(y(x),x$2)-diff(y(x),x)-6*x*y(x)
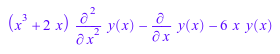
Мы вычисляем серийные решения в регулярной точке 1:
ode::series(Ly, y(x), x=1)
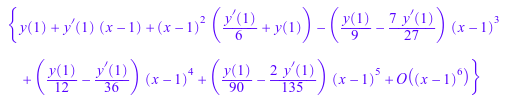
Серийные решения в регулярной особой точке 0:
ode::series(Ly, y(x), x=0)
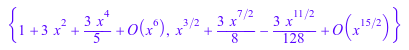
Также серийные решения в регулярной особой точке infinity:
ode::series(Ly, y(x), x=infinity)
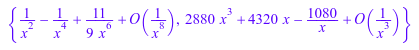
Рассмотрите следующее линейное дифференциальное уравнение:
Ly := x^2*diff(y(x),x$2)-x*diff(y(x),x)+(1-x)*y(x)
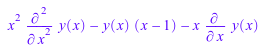
Мы вычисляем серийные решения в регулярной особой точке 0:
ode::series(Ly, y(x), x)
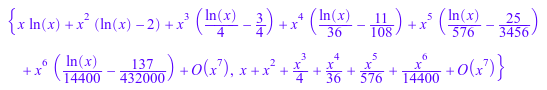
И в той же точке мы ищем решения, удовлетворяющие начальному условию y (0) = 1 и y (0) = 0:
ode::series({y(0)=1, Ly}, y(x), x)![]()
ode::series({y(0)=0, Ly}, y(x), x)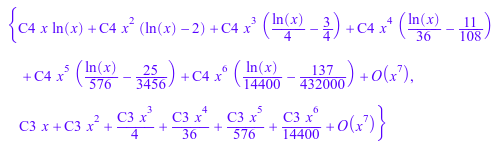
|
Обыкновенное дифференциальное уравнение. |
|
Зависимая функция |
|
Независимая переменная |
|
Точка расширения: арифметическое выражение. Если не заданный, точка 0 расширения по умолчанию используется. |
|
Начальные или граничные условия: последовательность уравнений. |
|
Количество условий, которые будут вычислены: неотрицательное целое число. Распоряжение по умолчанию дано переменной окружения |
Любой list, возможно, пустой, объектов типа Series::Puiseux или выражение типа "series".