ProjectorsСпроектируйте решение для ОДУ графических точек
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
| Обязательный | Список арифметических выражений |
| Объекты | Значения по умолчанию проекторов |
|---|---|
plot::Ode2d, plot::Ode3d |
Projectors задает “генераторы, отображают данные на графике”, что решение для проекта указывает (t, Y (t)) ОДУ к графическим точкам [x, y] в 2D или [x, y, z] в 3D, соответственно.
Внутренне, plot::Ode2d и plot::Ode3d сгенерируйте последовательность числовых точек решения (t 0, Y (t 0)), (t 1, Y (t 1)) и т.д. ОДУ. Каждый из этих, которые указывает решение, сопоставлен с графической точкой через “проекторы”, заданные Projectors.
Каждый проектор G i в Projectors = [[G1], [G2], …] список
[G i] =[(t, Y) -> [x(t,Y), y(t,Y), <z(t, Y)>], <Style = style>, <Color = color>] .
Процедуры (t, Y) -> [x(t, Y), y(t, Y), <z(t, Y)>] сопоставьте точки решения (t i, Y i) ОДУ к точкам [x (t i, Y i), y (t i, Y i)] в 2D (для plot::Ode2d) или [x (t i, Y i), y (t i, Y i), z (t i, Y i)] в 3D (для plot::Ode3d). Эти точки чертятся в изображении, интерполированном линейной интерполяцией или интерполяцией кубическим сплайном согласно атрибуту Style= style в наборе цветов атрибутом Color = color.
Параметр стиля может быть одним из флагов Points (только точки отображены), Lines (только интерполяция линейных сегментов отображена), Splines (только интерполирующая кубическая сплайновая кривая отображена), [Lines, Points] (интерполяция линейных сегментов вместе с точками интерполяции отображена), или [Splines, Points] (интерполирующая кубическая сплайновая кривая вместе с точками интерполяции отображена).
Стилем по умолчанию является Style= [Splines, Points].
Каждый из проекторов G 1, G 2 и т.д. (обозначенный G в следующем) является отображением
в 2D или
в 3D. Это должно принять числовой аргумент t и векторный Y (список или одномерный массив) и должно возвратить список числовых координатных значений [x, y] (в plot::Ode2d) или [x, y, z] (в plot::Ode3d), соответственно. Задавая соответствующие проекторы, любая информация о кривой решения ОДУ может быть отображена графически.
Вот некоторые примеры:
G := (t, Y) -> [t, Y[1]] создает 2D график первого компонента вектора решения вдоль y - ось, построенная против переменной t времени вдоль x - ось
G := (t, Y) -> [Y[1], Y[2]] создает 2D график фазы, строя первый компонент решения вдоль x - оси и второго компонента вдоль y - ось. Результатом является кривая решения в фазовом пространстве (параметризованный временем t).
G := (t, Y) -> [Y[1], Y[2], Y[3]] создает 3D график фазы первых трех компонентов кривой решения.
Если никакие проекторы не заданы в вызове plot::Ode2d, проекторы по умолчанию Generators = [[G1], [G2], …] используются, где
[G_i] = [(t, Y) -> [t, Y[i]], Style = [Splines, Points]].
Это строит i-th компонент вектора решения вдоль y - оси против “времени” t, построенный вдоль x - ось.
В plot::Ode3d, проекторы по умолчанию
[G_i] = [(t, Y) -> [t, Y[2*i - 1], Y[2*i]], Style = [Splines,Points]].
Это строит два из компонентов вектора решения вдоль y - и z - оси против “времени” t, построенный вдоль x - ось.
Мы рассматриваем 2-е ОДУ порядка
. Как динамическая система для
, ОДУ, которое будет решено,
.
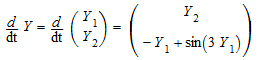Первый проектор G 1 график решение красного цвета как фаза в кривой (x, y) - плоскость.
Второй проектор G 2 графика kinectic энергия
зеленого цвета вдоль z - ось.
Третий проектор G 3 графика потенциальная энергия
синего цвета вдоль z - ось.
Четвертый проектор G 4 графика полная энергия черного цвета цвета вдоль z - ось:
f := (t, Y) -> [Y[2], - Y[1] + sin(3*Y[1])]:
Y0 := [0, 1]:
G1 := (t, Y) -> [Y[1], Y[2], 0]:
G2 := (t, Y) -> [Y[1], Y[2], Y[2]^2/2]:
G3 := (t, Y) -> [Y[1], Y[2], Y[1]^2/2 + cos(3*Y[1])/3]:
G4 := (t, Y) -> [Y[1], Y[2], Y[1]^2/2 + cos(3*Y[1])/3 + Y[2]^2/2]:
plot(plot::Ode3d(
f, [i/10 $ i = 0..100], Y0,
[G1, Style = Splines, Color = RGB::Red],
[G2, Style = Lines, Color = RGB::Green],
[G3, Color = RGB::Blue],
[G4, Style = [Lines, Points], Color = RGB::Black]))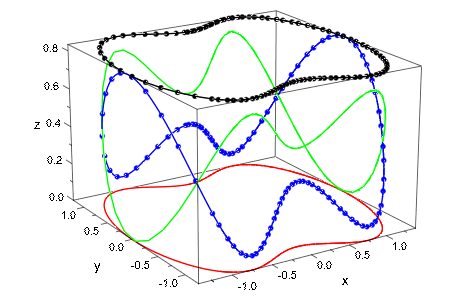
delete f, Y0, G1, G2, G3, G4: