`plot`::`Ode3d`

3D графики решений для ОДУ

Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.

Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.

Синтаксис

plot::Ode3d(f, [t₀, t₁, …], Y₀, <[G₁, <Style = style₁>, <Color = c₁>], [G₂, <Style = style₂>, <Color = c₂>], …>, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <a = a_min .. a_max>, options)
plot::Ode3d(f, [Automatic, t_start, t_end, t_step], Y₀, <[G₁, <Style = style₁>, <Color = c₁>], [G₂, <Style = style₂>, <Color = c₂>], …>, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <a = a_min .. a_max>, options)
plot::Ode3d([t₀, t₁, …], f, Y₀, <[G₁, <Style = style₁>, <Color = c₁>], [G₂, <Style = style₂>, <Color = c₂>], …>, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <a = a_min .. a_max>, options)
plot::Ode3d([Automatic, t_start, t_end, t_step], f, Y₀, <[G₁, <Style = style₁>, <Color = c₁>], [G₂, <Style = style₂>, <Color = c₂>], …>, <method>, <RelativeError = rtol>, <AbsoluteError = atol>, <Stepsize = h>, <a = a_min .. a_max>, options)

Описание

_{plot::Ode3d(f, [t0, t1,...], Y0)} представляет 3D проекции решений задачи с начальными значениями, данной f_t0 и _Y0.

_{plot::Ode3d(f, [t0, t1,...], Y0, [G])} вычисляет mesh числовых точек выборки Y (t ₀), Y (t ₁), … представление решения Y (t) дифференциального уравнения первого порядка (динамическая система)

Процедура

карты эти точки решения (t _i, Y (t _i)) в ℝ ×ℂⁿ к сетке 3D точек графика [x _i, y _i, z _i]. Эти точки могут быть соединены прямыми линиями или интерполирующими сплайнами.

Внутренне, последовательность числовых точек выборки

Y_1 := numeric::odesolve(f, t_0..t_1, Y_0, Options),

Y_2 := numeric::odesolve(f, t_1..t_2, Y_1, Options), и так далее

вычисляется, где Options некоторая комбинация method, RelativeError = rtol, AbsoluteError = atol, и Stepsize = h. Смотрите numeric::odesolve для получения дополнительной информации о векторной полевой процедуре f, начальное условие _Y0, и опции.

Служебная функция numeric::ode2vectorfield может использоваться, чтобы произвести входные параметры _{f, t0, Y0} от набора дифференциальных выражений, представляющих ОДУ.

Каждый из “генераторов данных о графике” _G1, _G2 и т.д. создает графическую кривую решения из числовых точек выборки _Y0, _Y1 и т.д. Каждый генератор G, Скажем, внутренне называется в форме _{G(t0, Y0), G(t1, Y1), …} произвести последовательность графика указывает в 3D.

Решатель numeric::odesolve возвращается решение указывает _Y0, _Y1, и так далее, как списки или одномерные массивы (фактический тип определяется начальным значением _Y0). Следовательно, каждый генератор G должен принять два аргумента (t, Y)T действительный параметр, Y “вектор” (или список или 1-мерный массив).

Каждый генератор должен возвратить список с 3 элементами, представляющими (x, y, z), координаты графической точки, сопоставленной с решением, указывают (t, Y) из ОДУ. Все генераторы должны произвести графические данные той же размерности, то есть, для plot::Ode3d, 3D данные как списки с 3 элементами. Например, G := (t, Y) -> [Y_1, Y_2, Y_3] создает 3D график фазы первых трех компонентов кривой решения.

Если никакие генераторы не даны, plot::Ode3d графиками по умолчанию каждая группа из двух компонентов как функции времени с тем же стилем.

Обратите внимание на то, что произвольные значения, сопоставленные с кривой решения, могут быть отображены графически соответствующим генератором G.

Несколько генераторов _{G1, G2}, и так далее, может быть задан, чтобы сгенерировать несколько кривых, сопоставленных с той же числовой mesh _{Y0, Y1, …}.

Графические данные, произведенные каждым из генераторов _{G1, G2,...} состоит из последовательности точек mesh в 3D.

С Style = Points, графические данные отображены как дискретный набор точек.
С Style = Lines, точки графических данных отображены как кривая, состоящая из сегментов прямой линии между точками выборки. Сами точки не отображены.
С Style = Splines, точки графических данных отображены как сглаженная сплайновая кривая, соединяющая точки выборки. Сами точки не отображены.
С Style = [Splines, Points] и Style = [Lines, Points], эффекты используемых стилей объединены, то есть, и точки оценки и прямые линии, или сплайны, соответственно, отображены.

Атрибуты графика приняты plot::Ode3d включайте Submesh = n, где n является некоторым положительным целым числом. Этот атрибут только оказывает влияние на кривые, которые возвращены для графических генераторов с Style = Splines и Style = [Splines, Points], соответственно. Это служит для сглаживания графической сплайновой кривой с помощью достаточно высокого количества точек графика.

n количество точек графика между двумя последовательными числовыми точками, соответствующими mesh времени. Значением по умолчанию является n = 4, то есть, сплайны построены как пять сегментов прямой линии, соединяющих числовые точки выборки.

Атрибуты

Атрибут	Цель	Значение по умолчанию
`AbsoluteError`	максимальная абсолютная ошибка дискретизации
`AffectViewingBox`	влияние объектов на `ViewingBox` из сцены	`TRUE`
`Colors`	список цветов, чтобы использовать	[`RGB::Blue`, `RGB::Red`, `RGB::Green`, `RGB::MuPADGold`, `RGB::Orange`, `RGB::Cyan`, `RGB::Magenta`, `RGB::LimeGreen`, `RGB::CadmiumYellowLight`, `RGB::AlizarinCrimson`, `RGB::Aqua`, `RGB::Lavender`, `RGB::SeaGreen`, `RGB::AureolineYellow`, `RGB::Banana`, `RGB::Beige`, `RGB::YellowGreen`, `RGB::Wheat`, `RGB::IndianRed`, `RGB::Black`]
`Frames`	количество систем координат в анимации	50
`Function`	выражение function или процедура
`InitialConditions`	начальные условия ОДУ
`Legend`	делает запись легенды
`LegendText`	короткий объяснительный текст для легенды
`LegendEntry`	добавить этот объект в легенду?	`FALSE`
`LineWidth`	ширина линий	0.35
`LineStyle`	тело, подчеркнутые штриховой линией или пунктирные линии?	`Solid`
`LinesVisible`	видимость линий	`TRUE`
`Name`	имя объекта графика (для браузера и легенды)
`ODEMethod`	числовая схема, используемая в том, что решила ОДУ	`DOPRI78`
`ParameterEnd`	закончите значение параметра анимации
`ParameterName`	имя параметра анимации
`ParameterBegin`	начальное значение параметра анимации
`ParameterRange`	область значений параметра анимации
`PointSize`	размер точек	1.5
`PointStyle`	стиль презентации точек	`FilledCircles`
`PointsVisible`	видимость точек mesh	`TRUE`
`Projectors`	спроектируйте решение для ОДУ графических точек
`RelativeError`	максимальная относительная ошибка дискретизации
`Stepsize`	установите постоянный размер шага
`Submesh`	плотность подmesh (дополнительные точки выборки)	4
`TimeEnd`	время окончания анимации	10.0
`TimeMesh`	числовая mesh времени
`TimeBegin`	время начала анимации	0.0
`TimeRange`	оперативный промежуток анимации	0.0.. 10.0
`Title`	объектный заголовок
`TitleFont`	шрифт объектных заголовков	[`" sans-serif "`, 11]
`TitlePosition`	положение объектных заголовков
`TitleAlignment`	выравнивание по горизонтали заголовков w.r.t. их координаты	`Center`
`TitlePositionX`	положение объектных заголовков, x компонент
`TitlePositionY`	положение объектных заголовков, y компонент
`TitlePositionZ`	положение объектных заголовков, z компонент
`USubmesh`	плотность дополнительных точек выборки для параметра “u”	4
`Visible`	видимость	`TRUE`
`VisibleAfter`	объект, видимый после этой временной стоимости
`VisibleBefore`	объект, видимый до этой временной стоимости
`VisibleFromTo`	объект, видимый в это время, располагается
`VisibleAfterEnd`	объект, видимый после его законченного времени анимации?	`TRUE`
`VisibleBeforeBegin`	объект, видимый перед его временем анимации, запускается?	`TRUE`

Примеры

Пример 1

Рассмотрите нелинейный генератор. Как динамическая система для, решите следующую задачу с начальными значениями, Y (0) = Y ₀:

f := (t, Y) -> [Y[2], sin(t) - Y[1]^3]: 
Y0 := [0, 0.5]:

Следующий генератор производит фазу в графике (x, y) плоскость, встроенная в 3D график:

G1 := (t, Y) -> [Y[1], Y[2], 0]:

Далее, используйте координату z 3D графика отобразить значение “энергетической” функции по кривой фазы:

G2 := (t, Y) -> [Y[1], Y[2], (Y[1]^2 + Y[2]^2)/2]:

Фаза изгибается (x, y), плоскость объединена с графиком энергетической функции:

p := plot::Ode3d(f, [i/5 $ i = 0..100], Y0,
                 [G1, Style = Splines, Color = RGB::Red],
                 [G2, Style = Points, Color = RGB::Black],
                 [G2, Style = Lines, Color = RGB::Blue]):

Установите явный размер точек, используемых в представлении энергии:

p::PointSize := 2*unit::mm:

Средство отображения называется:

plot(p, AxesTitles = ["y", "y'", "E"],
     CameraDirection = [10, -15, 5]):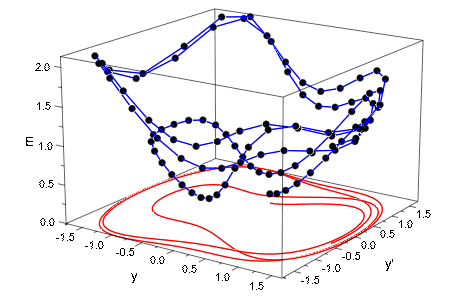

Пример 2

ОДУ Лоренца является системой

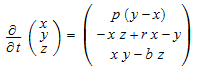
фиксированными параметрами p, r, b. Как динамическая система для Y = [x, y, z], решает ОДУ со следующим векторным полем:

f := proc(t, Y)
     local x, y, z;
     begin
        [x, y, z] := Y:
        [p*(y - x), -x*z + r*x - y, x*y - b*z]
     end_proc:

Считайте следующие параметры и следующее начальное условие Y0:

p := 10: r := 28: b := 1: 
Y0 := [1, 1, 1]:

Следующий генератор Gxyz производит 3D график фазы решения. Генератор Gyz проектирует кривую решения к (y, z) плоскость с x = 20; генератор Gxz проектирует кривую решения к (x, z) плоскость с y = - 15; генератор Gxy проектирует кривую решения к (x, y) плоскость с z = 0:

Gxyz := (t, Y) -> Y:
Gyz := (t, Y) -> [ 20,  Y[2], Y[3]]:
Gxz := (t, Y) -> [Y[1], -15,  Y[3]]:
Gxy := (t, Y) -> [Y[1], Y[2],   0 ]:

С этими генераторами создайте 3D объект графика, состоящий из кривой фазы и ее проекций.

object := plot::Ode3d(f, [i/10 $ i=1..100], Y0,
           [Gxyz, Style = Splines, Color = RGB::Red],
           [Gyz, Style = Splines, Color = RGB::Grey50],
           [Gxz, Style = Splines, Color = RGB::Grey50],
           [Gxy, Style = Splines, Color = RGB::Grey50],
           Submesh = 7):

Наконец, график представляется. Этот вызов является несколько трудоемким, потому что он вызывает числовой решатель numeric::odesolve произвести графические данные:

plot(object, CameraDirection = [-220, 110, 150])

Параметры

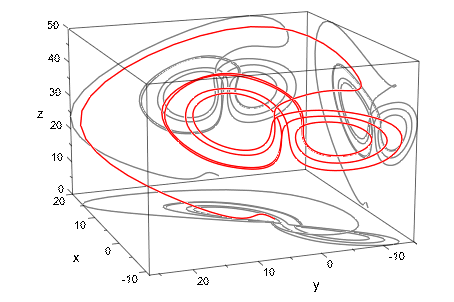
`f`	Векторное поле ОДУ: процедура. Смотрите `numeric::odesolve` для деталей. `f` эквивалентно атрибуту `Function`.
`_{t0, t1, …}`	Mesh времени: действительные численные значения. Если данные отображены с `Style = Splines`, эти значения должны быть в порядке возрастания. `_t0_t1`, … эквивалентен атрибуту `TimeMesh`.
`_tstart`, `_tend`, `_tstep`	Mesh времени: действительные численные значения. `_tend` должно быть больше, чем `_tstart` и `_tstep` должно быть положительным и должен быть меньшим, чем t _e nd - t _s tart. `_tstart`, `_tend`, `_tstep` эквивалентны атрибуту `TimeMesh`.
`_Y0`	Начальное условие ОДУ: список или 1-мерный массив. Смотрите `numeric::odesolve`. `_Y0` эквивалентно атрибуту `InitialConditions`.
`_{G1, G2, …}`	“генераторы отображают данные на графике”: процедуры, сопоставляющие решение, указывают `(t, Y(t))` к списку `[x, y]` или `[x, y, z]` представление графика указывает в 2D или 3D, соответственно. `_G1`, `_G2`, … эквивалентен атрибуту `Projectors`.
`method`	Используйте определенную числовую схему (см. `numeric::odesolve`)
`a`	Параметр анимации, заданный как `a` `_{= amin..amax}`, где `_amin` начальное значение параметров и `_amax` итоговое значение параметров.

Опции

`Style`	Опция, заданная как `Style = style` Устанавливает стиль, в котором отображены данные о графике. Следующие стили доступны: `PointsСтроки`, `Splines`, `[Lines, Points]`, и `[Splines, Points]`. Стилем по умолчанию является `[Splines, Points]`.
`Color`	Опция, заданная как `Color = c` Выбирает цвет RGB `c` в котором отображены данные о графике. Цветом по умолчанию i th генератор является i th запись атрибута `Colors`.
`RelErr`	Опция, заданная как `RelErr = rtol` Устанавливает числовой допуск дискретизации (см. `numeric::odesolve`)
`AbsErr`	Опция, заданная как `AbsErr = atol` Устанавливает числовой допуск дискретизации (см. `numeric::odesolve`)
`Stepsize`	Опция, заданная как `Stepsize = h` Устанавливает постоянный stepsize (см. `numeric::odesolve`)

Смотрите также

Функции MuPAD

numeric::ode2vectorfield | numeric::odesolve | numeric::odesolve2

MuPAD графические примитивы

plot::Curve2d | plot::Curve3d | plot::Ode2d | plot::PointList2d | plot::PointList3d | plot::Polygon2d | plot::Polygon3d | plot::Streamlines2d

Документация