ODEMethod, StepsizeЧисловая схема, используемая в том, что решила ОДУ
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
ODEMethodНеродной размер | Дополнительный | Выражение MuPAD® |
| Объекты | Значения по умолчанию |
|---|---|
plot::Ode2d, plot::Ode3d |
|
plot::Streamlines2d |
|
ODEMethod = method определяет числовую схему того, чтобы решить ОДУ. Параметр method имя, такое как EULER1, RK4, RKF78 и т.д.
Stepsize = h устанавливает постоянный размер шага h, который используется для расчета числовое решение.
Внутренне, plot::Ode2d, plot::Ode3d, и plot::Streamlines2d вызовите стандартный numeric::odesolve для того, чтобы решить данный ОДУ численно. Метод, установленный атрибутом ODEMethod = method и/или размер шага установлен Stepsize = h передаются numeric::odesolve. Смотрите соответствующую страницу справки для полного списка всех доступных методов и для получения дальнейшей информации на размере шага.
Установка ODEMethod = ABM4 исключение к вышеупомянутому: Это только доступно с plot::Streamlines2d и заставляет график использовать быстрый интегратор корректора предиктора Адамса-Бэшфорта-Маултона четвертого порядка с фиксированным размером шага. Это игнорирует настройки RelativeError и AbsoluteError.
Мы решаем задачу с начальными значениями
численно согласно классическому 4-му порядку схема Runge-Kutta RK4 использование постоянного размера шага 0.1:
f := (t, Y) -> [-Y[1]]:
Y0 := [1]:
timemesh:= [0, 1, 2, 3, 4, 5]:
plot(plot::Ode2d(f, timemesh, Y0, ODEMethod = RK4,
Stepsize = 0.1))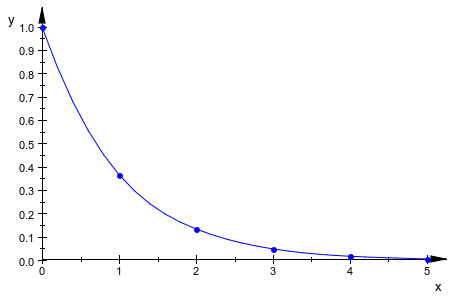
delete f, Y0, timemesh:
С настройками по умолчанию, plot::Streamlines2d не может построить векторное поле
(который не является непрерывным Липшицом) удовлетворяющим способом:
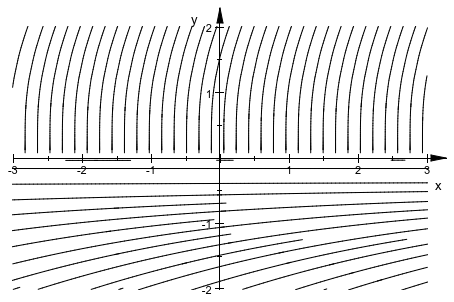
plot(plot::Streamlines2d([1, surd(3,y)^2],
x=-3..3, y=-2..2))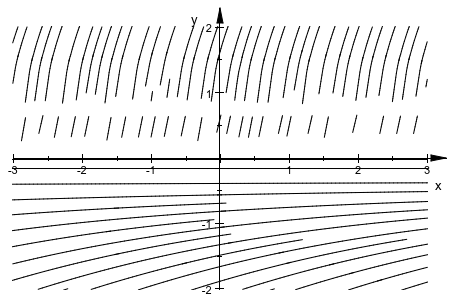
При помощи различного числового интегратора проблемы могут быть преодолены (за счет более длительного расчета):
plot(plot::Streamlines2d([1, surd(3,y)^2],
x=-3..3, y=-2..2,
ODEMethod=RKF43,
RelativeError=1e-3))