recОбласть уравнений повторения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
rec(eq, y(n), <cond>)
rec(eq, y(n)) создает объект типа rec представление уравнения повторения для последовательности y(n).
Уравнение eq должен включить только переключает y(n + i) с целочисленными значениями i; по крайней мере одно такое выражение должно присутствовать в eq. Арифметический expressioneq эквивалентно уравнению eq = 0.
Начальные или граничные условия cond должен быть задан как системы уравнений формы {y(n0) = y0, y(n1) = y1, ...} с арифметическими выражениями n0, n1, ... это не должно содержать идентификатор n, и арифметические выражения y0, y1, ... это не должно содержать идентификатор y.
Основная цель rec область должна обеспечить среду для перегрузки функционального solve. Для повторения r из типа rec, вызов solve(r) возвращает набор, представляющий аффинное подпространство пробела полного решения. Его единственная запись является выражением в n это может содержать свободные параметры, такие как C1C2 , и т.д. SeeExample 1, Пример 4 и Пример 5.
В настоящее время только линейные повторения с коэффициентами, которые являются рациональными функциями n может быть решен. solve повторения указателей с постоянными коэффициентами, это находит гипергеометрические решения повторений первого порядка и полиномиальные решения повторений высшего порядка с непостоянными коэффициентами.
solve не всегда может найти пробел полного решения. См. Пример 5. Если solve не может найти решение, затем solve на звонок отвечают символически. Для параметрических повторений, выхода solve может быть условно заданный набор типа piecewise. См. пример 6.
Первая команда определяет гомогенное уравнение повторения первого порядка
для последовательности y (n). Это решено вызовом solve функция:
rec(y(n + 1) = 2*y(n)*(n + 1)/n, y(n))
solve(%)
Таким образом общим решением уравнения повторения является y (n) = C 1 n 2n, где C 1 является произвольной постоянной.
В следующем примере гомогенное повторение первого порядка y (n + 1) = 3 (n + 1) y (n) с начальным условием y (0) = 1 решен для неизвестной последовательности y (n):
solve(rec(y(n + 1) = 3*(n + 1)*y(n), y(n), {y(0) = 1}))
Таким образом решением является
для всех целых чисел n ≥ 0 (gamma является гамма функцией).
В следующем примере неоднородное повторение второго порядка y (n + 2) - 2 y (n + 1) + y (n) = 2 решен для неизвестной последовательности y (n). Начальные условия y (0) = - 1 и y (1) = m некоторым параметром m учтены solve:
solve(rec(y(n + 2) - 2*y(n + 1) + y(n) = 2, y(n),
{y(0) = -1, y(1) = m}))
Мы вычисляем общее решение гомогенного повторения второго порядка y (n + 2) + 3 y (n + 1) + 2 y (n) = 0:
solve(rec(y(n + 2) + 3*y(n + 1) + 2*y(n), y(n)))
Здесь, C6 и C7 произвольные постоянные.
Для следующего гомогенного третьего повторения порядка с непостоянными коэффициентами система только находит полиномиальные решения:
solve(rec(n*y(n + 3) = (n + 3)*y(n), y(n)))
Следующее гомогенное повторение второго порядка с постоянными коэффициентами включает параметр a. Набор решения зависит от значения этого параметра и solve возвращает piecewise объект:
solve(rec(a*y(n + 2) = y(n), y(n)))
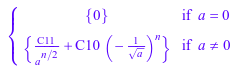
Следующее гомогенное повторение второго порядка с непостоянными коэффициентами включает параметр a. Несмотря на то, что это имеет полиномиальное решение для a = 2, система не распознает это:
solve(rec(n*y(n + 2) = (n + a)*y(n), y(n)))
|
Уравнение или арифметическое выражение |
|
Неизвестная функция: идентификатор |
|
Индекс: идентификатор |
|
Набор начальных или граничных условий |
Объект типа rec.
Для гомогенных повторений с постоянными коэффициентами, solve вычисляет корни характеристического полинома. Если некоторым из них нельзя дать в явной форме, т.е. только посредством RootOf, затем solve не возвращает решение. В противном случае пробел полного решения возвращен.
Для первого порядка гомогенные повторения с непостоянными коэффициентами, solve возвращает пробел полного решения, если коэффициенты повторения могут быть включены в в большинстве квадратичных полиномов. В противном случае, solve не возвращает решение.
Для гомогенных повторений порядка по крайней мере два с непостоянными коэффициентами, solve находит полный пробел всех полиномиальных решений.
В настоящее время неоднородные повторения могут только быть решены, если у них есть полиномиальное решение. Предыдущие комментарии применяются.
Для параметрических повторений система не может найти решения, которые допустимы только для специальных значений параметров. См. Пример 7.