odeОбласть обыкновенных дифференциальных уравнений
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
ode(eq,y(x)) ode({eq, <inits>},y(x)) ode({eq1, eq2, , …, <inits>},{y1(x), y2(x), …})
ode(eq, y(x)) представляет обыкновенное дифференциальное уравнение (ODE) для функционального y(x).
ode({eq1, eq2, ...}, {y1(x), y2(x), ...}) представляет систему ОДУ для функций y1(x), y2(x) и т.д.
В уравнениях eq, eq1 и т.д. неизвестные функции должны быть представлены y(x), y1(x) и т.д. Производные могут быть представлены любой diff функционируйте или дифференциальным оператором D. Обратите внимание на то, что маркерный ' обеспечивает удобный ярлык: y'(x) = D(y)(x) означает то же самое как diff(y(x), x).
Неизвестные функции должны быть одномерными в независимой переменной x. Многомерные выражения, такие как y(x, t) не приняты.
ode функция не принимает piecewise входной параметр.
Начальные и граничные условия заданы последовательностями уравнений, включающих неизвестные функции или их производные на левой стороне. Соответствующие значения должны быть заданы на правой стороне уравнений. В частности, дифференциальный оператор D (или маркерный ') должен использоваться, чтобы задать значения производных в какой-то момент. Например,
![]()
допустимая последовательность граничных условий для inits.
Граничные условия первого и второго вида позволены. Смешанные условия не приняты.
Начальная буква/граничные точки и соответствующая начальная буква/граничные значения могут быть символьными выражениями.
Для скалярного начального значения или краевых задач, используйте ode({eq, inits}, y(x)) задавать условия.
Для систем ОДУ должно быть столько же уравнений сколько неизвестные функции.
Основная цель ode область должна обеспечить среду для перегрузки функционального solve.
В случае одного одного уравнения (возможно вместе с начальными или граничными условиями), solve возвращает набор явных решений или неявного решения. Каждый элемент набора представляет ветвь решения.
В случае системы уравнений, solve возвращает набор списков уравнений для неизвестных функций. Каждый список представляет ветвь решения.
Символьный solve на звонок отвечают, если никакое решение не найдено.
В следующем мы показываем, как создать и решить скалярный ОДУ. Во-первых, мы задаем ОДУ![]() . Мы используем лексему кавычки
. Мы используем лексему кавычки ' представлять производные:
eq := ode(x^2*y'(x) + 3*x*y(x) = sin(x)/x, y(x))
![]()
Мы получаем элемент доменного ode который мы можем теперь решить:
solve(eq)
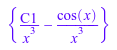
delete eq:
Задача с начальными значениями задана как набор, состоящий из ОДУ и начальных условий:
ivp := ode({f''(t) + 4*f(t) = sin(2*t),
f(0) = a, f'(0) = b}, f(t))![]()
solve(ivp)
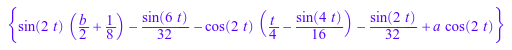
delete ivp:
С некоторыми ограничениями также возможно решить системы ОДУ. Во-первых, задайте систему:
sys := {x'(t) - x(t) + y(t) = 0, y'(t) - x(t) - y(t) = 0}![]()
Вызов solve дает к общему решению произвольными параметрами:
solution := solve(ode(sys, {x(t), y(t)}))![]()
Чтобы проверить результат, замените им назад в систему sys. Однако для замены, необходимо переписать систему в обозначение с помощью diff функция:
eval(subs(rewrite(sys, diff), op(solution)))
![]()
delete sys, solution:
Если вы имеете систему дифференциальных уравнений в матричной форме, извлекаете компоненты матрицы к набору дифференциальных уравнений:
Y:= matrix([x(t), y(t)]):
A:= matrix([[1, 2], [-1, 6]]):
s := ode({op(diff(Y, t) - A*Y)}, {x(t), y(t)})![]()
Теперь используйте solve функция, чтобы решить систему:
solve(s)
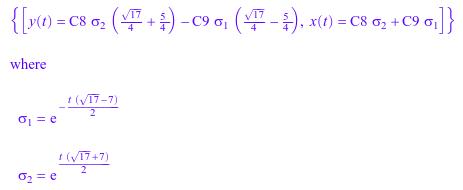
В этом примере мы указываем на различные форматы возврата odeрешите средство. Во-первых, мы решаем ОДУ с начальным условием. Решение включает символьный интеграл:
solve(ode({y'(x) + x*y(x) = cos(x), y(0) = 3}, y(x)))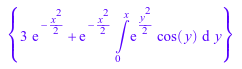
Для следующего уравнения мы получаем неявное решение:
solve(ode((x*y'(x) - y(x))^4*exp(x*y'(x) - y(x))
- ln(x*y'(x) - y(x)), y(x)))![]()
Это - алгебраическое уравнение для y. Его решение задает y как функция x и произвольный параметр C сопровождаемый номером, автоматически сгенерированным MuPAD® (постоянный из интегрирования). Однако алгебраическое уравнение не имеет решения в закрытой форме.
delete sys, solution:
Это может произойти, что MuPAD не может решить данное уравнение. В таком случае, символьном solve команда возвращена:
solve(ode(x*diff(y(x),x)-y(x)*(x*ln(x^3/y(x))+2), y(x)))
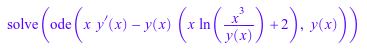
Решатель ОДУ MuPAD содержит алгебраические алгоритмы для вычисления Liouvillian и non-Liouvillian решений линейных обыкновенных дифференциальных уравнений. Эти алгоритмы основаны на дифференциале теория Галуа и на дополнительных методах для нахождения решений линейных обыкновенных дифференциальных уравнений, данных в терминах специальных функций. Для примера известного Ковэкика
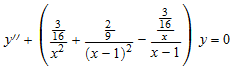 ,
,
решение может быть найдено как:
solve(ode(y''(x) + (3/(16*x^2) + 2/(9*(x - 1)^2)
- 3/(16*x*(x - 1)))*y(x), y(x)))![]()
MuPAD может найти Liouvillian и non-Liouvillian решения для уравнений высшего порядка также. Однако в случае решений Liouvillian, нет никакой гарантии, что все они найдены.
MuPAD также находит non-Liouvillian решения в терминах функции Бесселя, Эйри и функций Уиттекера:
eq := y'(x) + y(x)^2 + b + a*x
![]()
solve(ode(eq, y(x)))

Мы проверяем это решение:
simplify(eval(subs(rewrite(eq, diff), y(x) = op(%))))
![]()
Также возможно вычислить серийные решения обыкновенного дифференциального уравнения (cf. ode::series для получения дальнейшей информации):
series(ode(y''(x) + 4*y(x) = sin(w*x), y(x)), x = 0, 8)
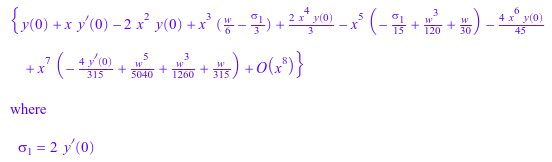
|
Уравнения или арифметические выражения в неизвестных функциях и их производных относительно |
|
Неизвестные функции: идентификаторы |
|
Независимая переменная: идентификатор |
|
Начальные или граничные условия: последовательность уравнений |
Объект типа ode.
[1] Э. Камк. “Differentialgleichungen: Lösungmethoden und Lösungen”. Б.Г. Теубнер, Штутгарт, 1997.
[2] Г.М. Мерфи. “Обыкновенные дифференциальные уравнения и их решения”. Ван Нострэнд, Принстон, 1960.
[3] Д. Цвиллингер. “Руководство дифференциальных уравнений”. Сан-Диего: Academic Press, 1992.
[4] В. Фэклер. Algebraische Algorithmen zur Lösung von linearen Differentialgleichungen. Штутгарт, Лейпциг: Teubner, Отчеты Reihe MuPAD, 1999.
[5] М. ван дер Пут и М.Ф. Зингер. “Теория Галуа линейных дифференциальных уравнений”. Grundlehren der Mathematischen Wissenschaften, 328, Springer-Verlag, Берлин, 2003.
[6] Ф. Алмер и М.Ф. Зингер. Liouvillian и алгебраические решения вторых и третьих линейных дифференциальных уравнений порядка. “Дж. Симб. Аккомпанируйте”, 16:37-74, 1993.