Пример 1

Первое правило представляет упрощение sin(X)^2 + cos(X)^2 = 1. Первый аргумент правила является выражением sin(X)^2 + cos(X)^2. Каждое выражение, которое имеет ту же структуру, найдено match, и второй аргумент правила 1 возвращен как результат. Нет никаких условий для валидности этой эквивалентности. Идентификаторы, используемые в определении правила, защищаются от записи, потому что у них есть имена, начинающиеся с #:

r := Rule(sin(`#X`)^2 + cos(`#X`)^2, 1):
Rule::apply(r, sin(2*x - 1)^2 + cos(2*x - 1)^2)

Следующее выражение не имеет правильной формы, приложения сбоев правила:

Rule::apply(r, sin(2*x - 1)^2 + cos(2*x + 1)^2)

Пример 2

Следующее правило представляет теорему сложения sin(X + Y) = sin(X)*cos(Y) + sin(Y)*cos(X). Первый аргумент правила является выражением sin(X + Y). Каждое выражение, которое является вызовом sin с суммой в качестве аргумента, идентифицирован match, и сумма sin(X)*cos(Y) + sin(Y)*cos(X) возвращен, где X и Y заменяются соответствующими частями данного выражения. Нет никаких условий для валидности этой эквивалентности. Вторая часть правила предотвращена от оценки с hold. Идентификаторы, используемые в определении правила, защищаются от записи, потому что у них есть имена, начинающиеся с #:

r := Rule(sin(`#X` + `#Y`),
          hold(sin(`#X`)*cos(`#Y`) + sin(`#Y`)*cos(`#X`))):
Rule::apply(r, sin(tan(x) + tan(y)))

matcher идентифицирует различие двух выражений a и b как сумма a + -b, поэтому также следующий пример работает:

Rule::apply(r, sin(tan(x) - tan(y)))

Пример 3

Мы задаем два правила на основе тригонометрического identies sin (x) ² = 1 - cos (x) ² и:

myrules := [Rule(sin(`#X`)^`#n`, (1 - cos(`#X`)^2)^(`#n`/2),
                         {`#n` -> is(`#n`, Type::Even)}),
            Rule(tan(`#X`)^`#n`, (1/cos(`#X`)^2 - 1)^(`#n`/2),
                            {`#n` -> is(`#n`, Type::Even)})
            ]:

Мы хотим применить эти правила как переписывающие правила к различным выражениям. Мы передаем Rule::apply ко всем подвыражениям выражения через misc::maprec. Для удобства, функция интерфейса myrewrite реализован, который вызывает misc::maprec:

myrewrite:= proc(f, rules)
local _rewrite;
begin
   _rewrite:= proc(x)
   local r, tmp;
   begin
      for r in rules do
         tmp:= Rule::apply(r, x);
         if tmp <> FAIL then
            x:= tmp;
         end;
      end;         
      return(x)
    end;
    misc::maprec(f, TRUE = _rewrite);
end:

Теперь мы можем вызвать myrewrite(f, myrules) применять правила перезаписи к выражению f:

f:= tan(x) + sin(2*x) - tan(y)^2*sin(x + 3)^6 + sin(x)^2 * tan(23)^4:
myrewrite(f, myrules);

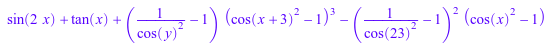
delete myrules, myrewrite, f:

Пример 4

Другое правило представляет упрощение sin(X) = 0, который только верен, когда X целочисленное кратное PI:

r := Rule(sin(`#X`), 0, {`#X` -> is(`#X`/PI, Type::Integer)}):
Rule::apply(r, sin(2*x*PI))

В последней возможности, аргументе sin не имеет необходимого свойства, таким образом, приложение сбоев правила.

После предположения x, выражение имеет правильную форму:

assume(x, Type::Integer):
Rule::apply(r, sin(2*x*PI))

Следующее приложение правила проверяет константное выражение:

Rule::apply(r, sin(2*PI))

Почему FAIL? Проблема, sin упрощает постоянный вход 2*PI к 0 самостоятельно, таким образом, правило получает 0 как введено. Однако 0 не имеет необходимой формы, таким образом, FAIL возвращен.

Пример 5

Другое правило представляет упрощение ln(neg^even*r) = even*ln(-neg) + ln(r), который только верен, когда neg отрицательно и even четное число:

r := Rule(ln(`#Neg`^`#Even`*`#X`),
          `#Even`*ln(-`#Neg`) + ln(`#X`),
          {`#Neg` -> is(`#Neg`, Type::Negative) = TRUE,
           `#Even` -> is(`#Even`, Type::Even) = TRUE}):
delete e, n, x:
Rule::apply(r, ln(n^e*x))

Сбои приложения правила, потому что переменные не имеют необходимых свойств.

С предположением n должна быть отрицательная переменная и e должно быть ровным:

assume(n < 0): assume(e, Type::Even):
Rule::apply(r, ln(n^e*x))

Пример 6

Это правило представляет приложение rewrite к выражению с целевым exp, когда выражение имеет подвыражения типа "sin" или "cos". Первый аргумент правила является процедурой, которая вызывает rewrite с любым выражением и целевым exp и возвращает выражение, эквивалентное входу (потому что rewrite он). Второй аргумент является процедурой, которая проверяет, ли sin или cos содержится во входном выражении:

r := Rule(X -> rewrite(X, exp), X -> has(X, sin) or has(X, cos)):
Rule::apply(r, sin(2*x - 1)^2 + cos(2*x - 1)^2)

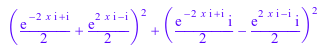
Следующее выражение не имеет sin или cos, так приложение сбоев правила:

Rule::apply(r, tan(2*I*x))

Пример 7

Это правило представляет приложение rewrite к выражению с несколькими целями. Первый аргумент правила является процедурой, которая применяет rewrite к данному выражению, с целью в зависимости от входа. Это правило не имеет процедуры условия:

rewProc :=
  proc(ex)
  begin
    rewrite(ex, (if has(ex, exp) then
                   tan
                 elif has(ex, sin) or has(ex, cos) then
                   cot
                 elif has(ex, tan) or has(ex, cot) then
                   sincos
                 else
                   exp
                 end_if))
  end_proc:
r := Rule(rewProc):
Rule::apply(r, exp(2*x))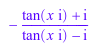

Правило применяется снова к последнему результату:

Rule::apply(r, %)

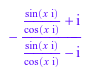
Последний результат должен быть упрощен назад до первого выражения:

Simplify(%)

Пример 8

Новый Simplify использует основу правила в применении большой перезаписи правил для нахождения самой простой формы любого данного выражения.

Мы хотим переписать только некоторые степени и принять, что все используемые переменные действительны (не используя свойства).

Список PowerRules состоит из нескольких правил. Процедура powerRules возвращается все это управляет в списке.

Из-за лучшей удобочитаемости имена используемых идентификаторов коротки и не защищенные имена:

PowerRules :=
  [Rule(A^m*A^n, hold(A^(m + n))),
   Rule(A^m/A^n, hold(A^(m - n))),
   Rule(A^n*B^n, hold((A*B)^n)),
   Rule(A^n/B^n, hold((A/B)^n)),
   Rule(A^n/B^n, hold((B/A)^-n)),
   Rule((A^m)^n, hold(A^(m*n)))]:
powerRules := proc()
              begin
                PowerRules
              end_proc:

Simplify вызван опцией SelectRules, и ожидает процедуру, которая возвращает список правил, применимых к данному выражению. В этом случае все правила возвращены в каждом случае.

Simplify применяет все правила к данному выражению и также к переписанным результатам и пытается найти самую легкую форму выражения относительно процедуры оценки по умолчанию Simplify::complexity.

Из-за аргумента SelectRules = powerRules, только данные правила использованы Simplify:

Simplify(T^(1/2)*(R*T)^(-1/2), SelectRules = powerRules)

Другие выражения не могут быть упрощены с той же основой правила:

Simplify(sin(x)^2 + cos(x)^2, SelectRules = powerRules)

delete r, x, powerRules, PowerRules: