rewriteПерепишите выражение
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
rewrite(f, target)
rewrite(f, target) преобразовывает выражение f к математически эквивалентной форме, пытаясь выразить f в терминах заданной целевой функции.
Цель указывает на функцию, которая должна использоваться в желаемом представлении. Символьные вызовы функции в f заменяются целевой функцией, если это математически допустимо.
С целевым arg, функциональный ln(sign(x)) переписан как i arg (x).
С целевым exp, все тригонометрические и гиперболические функции переписаны в терминах exp. Далее, обратные функции, а также arg переписаны в терминах ln.
С целевым sincos, функции tanраскладушкаexpsinhдубинкаtanh, и coth переписаны в терминах sin и cos.
С целевым sin, то же самое сделано как в случае sincos. Кроме того, cos (x) 2 переписан как 1 - sin (x) 2. Это содержит для целевого cos аналогично.
С целевым sinhcosh, функции exptanhcoth, sinпотому чтоtan, и cot переписаны в терминах sinh и cosh. С целями sinh и cosh, то же самое сделано, и cosh(x)^2 переписан в терминах sinh (или sinh(x)^2 в терминах cosh, соответственно.)
С целями arcsin, arccos, arctan, и arccot, логарифм, все обратные тригонометрические функции и все обратные гиперболические функции переписаны в терминах целевой функции.
С целями arcsinh, arccosh, arctanh, и arccoth, логарифм, все обратные гиперболические функции и все обратные тригонометрические функции переписаны в терминах целевой функции.
С целевым lambertW, функциональный wrightOmega переписан в терминах lambertW.
С целевым erf, функции erfc, erfi, и dawson переписаны в терминах erf.
С целевым erfc, функции erf, erfi, и dawson переписаны в терминах erfc.
С целевым erfi, функции erferfc, и dawson переписаны в терминах erfi.
С целевым bernoulli, функциональный euler переписан в терминах bernoulli.
С целевым diff, символьные вызовы дифференциального оператора D переписаны в терминах символьных вызовов функционального diff. Например, D(f)(x) преобразован в diff(f(x), x). Одномерное выражение D(f)(x) переписан если x идентификатор или индексируемый идентификатор. Многомерное выражение D([n1, n2, ...], f)(x1, x2, ...) переписан если x1x2 отличные идентификаторы или индексированные идентификаторы. Попытка переписать многомерный вызов D(f)(x1, x2, ...) из одномерного dervative D(f) повышает ошибку.
С целевым D, символьный diff вызовы переписаны в терминах дифференциального оператора D. Производные одномерных вызовов функции, такие как diff(f(x), x) переписаны как D(f)(x). Производные многомерных вызовов функции выражаются через D([n1, n2, ...], f). Например, diff(f(x, y), x) переписан как D([1], f)(x, y).
С целевым andor, логические операторы xor, ==>, и <=> переписаны в терминах and, or, и not.
С целями min и max, выражения в max и min и, для действительных аргументов, abs переписаны в терминах целевой функции.
Цели harmonic и psi служите для перезаписи символьных вызовов psi в терминах harmonic и наоборот.
С целевым inverf, функциональный inverfc(x) переписан как inverf(1 - x).
С целевым inverfc, функциональный inverf(x) переписан как inverfc(1 - x).
Этот пример демонстрирует использование rewrite:
rewrite(D(D(f))(x), diff)
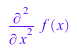
diff(f(x, x), x) = rewrite(diff(f(x, x), x), D)
![]()
assume(n, Type::PosInt): rewrite(fact(n), gamma), rewrite(gamma(n), fact); delete n:
![]()
rewrite(sign(x), heaviside), rewrite(heaviside(x), sign);
![]()
rewrite(heaviside(x), piecewise)
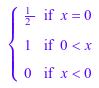
Тригонометрические функции могут быть переписаны в терминах exp, sinпотому что и т.д.:
rewrite(tan(x), exp), rewrite(cot(x), sincos), rewrite(sin(x), tan)
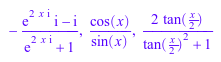
rewrite(arcsinh(x), ln)
![]()
Обратные тригонометрические функции могут быть переписаны друг в терминах друга:
rewrite(arcsin(x), arctan)
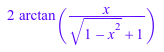
Следующий результат использует функциональный signIm (“знак мнимой части”), чтобы сделать формулу допустимой в комплексной плоскости (кроме сингулярности в![]() ):
):
rewrite(arctan(x), arcsin)

| |
|
Целевая функция, которая будет использоваться в представлении: один из |
f