stats::gammaPDFФункция плотности вероятности гамма распределения
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
stats::gammaPDF(a, b)
stats::gammaPDF(a, b) возвращает процедуру, представляющую функцию плотности вероятности
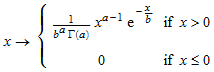
из гамма распределения параметром формы a> 0 и масштабный коэффициент b> 0.
Процедура f:=stats::gammaPDF(a, b) может быть назван в форме f(x) с арифметическим выражением x. Возвращаемое значение f(x) или число с плавающей запятой или символьное выражение:
Если x ≤ 0 может быть решен, то f(x) возвращается 0. Если x> 0 может быть решен, то f(x) возвращает значение![]() .
.
Если x является числом с плавающей запятой, и и a и b могут быть преобразованы в положительные числа с плавающей запятой, то эти значения возвращены как числа с плавающей запятой. В противном случае символьные выражения возвращены.
Функциональный f реагирует на свойства набора идентификаторов через assume. Если x является символьным выражением со свойством x ≤ 0 или x ≥ 0, соответствующие значения возвращены.
f(- infinity ) и f( infinity ) return 0.
f(x) отвечает на символьный звонок stats::gammaPDF(a, b)(x) если ни x ≤ 0, ни x> 0 не могут быть решены.
Численные значения для a и b только приняты, если они действительны и положительны.
Обратите внимание на то, что, для большого a, точные результаты могут быть дорогостоящими, чтобы вычислить. Если значения с плавающей точкой желаемы, рекомендуется передать аргументы x с плавающей точкой к f вместо того, чтобы вычислять точные результаты f(x) и преобразуйте их через float. См. пример 4.
Обратите внимание на то, что![]() .
.
Функция чувствительна к переменной окружения DIGITS который определяет числовую рабочую точность. Процедура сгенерирована stats::gammaPDF реагирует на свойства набора идентификаторов через assume.
Мы оцениваем функцию плотности вероятности с a = 2 и b = 1 в различных точках:
f := stats::gammaPDF(2, 1): f(-infinity), f(-PI), f(1/2), f(0.5), f(PI), f(infinity)
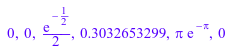
delete f:
Если x символьный объект без свойств, затем нельзя решить, содержит ли x ≥ 0. Возвращен символьный вызов функции:
f := stats::gammaPDF(a, b): f(x)
![]()
С подходящими свойствами можно решить, содержит ли x ≥ 0. Возвращено явное выражение:
assume(0 < x): f(x)
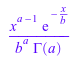
unassume(x): delete f:
Мы используем символьные аргументы:
f := stats::gammaPDF(a, b): f(x), f(3)
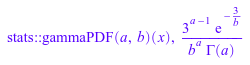
Когда численные значения присвоены a и b, функциональный f начинает приводить к числовым результатам:
a := 2: b := 4: f(3), f(3.0)

delete a, b, f:
Мы рассматриваем гамма распределение большим параметром формы:
f := stats::gammaPDF(2000, 2):
Для приближений с плавающей точкой не нужно вычислять точный результат и преобразовывать его через float. Для большого параметра формы это быстрее, чтобы передать аргумент с плавающей точкой f. Следующий вызов занимает время, потому что![]() включен точный расчет огромного целого числа:
включен точный расчет огромного целого числа:
float(f(4050))
![]()
Следующий вызов намного быстрее:
f(float(4050))
![]()
delete f:
|
Параметр формы: арифметическое выражение, представляющее положительное действительное значение |
|
Масштабный коэффициент: арифметическое выражение, представляющее положительное действительное значение |