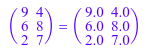Документация

Разложение Холесского

Разложение Холесского Эрмитовой (самопримыкающей) положительной определенной матрицы является продуктом нижнего треугольного матричного L и его Эрмитовы транспонируют L ^H: A = L  L^H. Эрмитовы транспонируют матрицы, сопряженное комплексное число транспонировать. Для действительных симметричных положительных определенных матриц, A = L  L^T, где L ^T является транспонированием L.

Можно выполнить факторизацию Холесского комплексных матриц символически при помощи linalg::factorCholesky или численно при помощи numeric::factorCholesky. Например, создайте следующее 2×2 матрица:

A := matrix([[sin(1), I], [-I, exp(2)]])

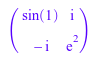
Во-первых, вычислите разложение Холесского той матрицы при помощи символьного linalg::factorCholesky функция:

L := linalg::factorCholesky(A)

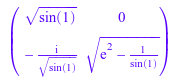
Теперь вычислите разложение Холесского при помощи символьного numeric::factorCholesky функция:

L := numeric::factorCholesky(A)

При использовании numeric::factorCholesky, можно предотвратить преобразование данных к числам с плавающей запятой и, поэтому, получить символьный результат при помощи Symbolic опция:

L := numeric::factorCholesky(A, Symbolic)

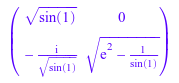
Продукт треугольной матрицы L и его Эрмитовы транспонируют, дает исходный матричный A:

testeq(A = L*htranspose(L))

LU-разложение

LU-факторизация выражает m ×n матричный A как продукт нижнего треугольного матричного L и верхняя треугольная матрица U: A = L  U. Кроме того, LU-разложение может включить матрицу перестановок строки: P  A = L  U. Чтобы вычислить LU-разложение матрицы численно, используйте numeric::factorLU функция. Например, создайте следующее 4×4 матрица Теплица:

T := linalg::toeplitz(4, [1, 2, 3, 4, 5])

Используйте numeric::factorLU функция, чтобы вычислить LU-разложение матричного T численно:

[L, U, p] := numeric::factorLU(T)

Вместо того, чтобы возвратить матрицу перестановок P, MuPAD^® возвращает список p с числами, соответствующими строке, обменивается в матричном T. Для n ×n матрица, список p представляет следующую матрицу перестановок с индексами i и j в пределах от 1 к n:

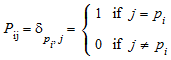Используя это выражение, восстановите матрицу перестановок P из списка p:

P := matrix(4, 4):
for i from 1 to 4 do
   P[i, p[i]] := 1
end_for:
P

Более эффективно вычислите результат применения матрицы перестановок к A не восстанавливая саму матрицу перестановок:

PT := matrix(4, 4):
for i from 1 to 4 do
  PT[i, 1..4] := T[p[i], 1..4]
end_for:
PT

В точности с плавающей точкой, продукте нижнего треугольного матричного L и верхняя треугольная матрица U исходный матричный A со строками, которыми обмениваются согласно матрице перестановок P:

float(PT) = L*U

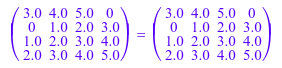
Символьная функция LU-факторизации использует различную вертящуюся стратегию, чем числовая функция LU-факторизации. Поэтому символьная функция может возвратить различные результаты для той же матрицы:

linalg::factorLU(T)

Разложение QR

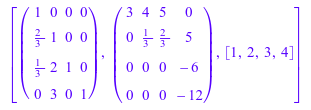
QR-факторизация выражает m ×n матричный A можно следующим образом: A = Q*R. Здесь Q m ×m унитарная матрица и R m ×n верхняя треугольная матрица. Если компоненты A вещественные числа, Q ортогональная матрица. Чтобы вычислить разложение QR матрицы численно, используйте numeric::factorQR функция. Например, создайте следующее 3×3 матрица Вандермонда:

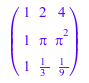
V := linalg::vandermonde([2, PI, 1/3])

При вычислении разложения QR той матрицы символически, вы получаете следующий длинный результат:

[Q, R] := linalg::factorQR(V)

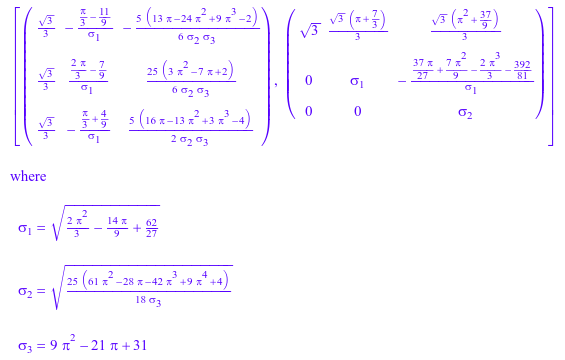
Чтобы получить более короткий ответ, аппроксимируйте этот результат числами с плавающей запятой:

[Q, R] := float([Q, R])

Можно получить тот же результат быстрее путем вызывания числовой функции факторизации с начала:

[Q, R] := numeric::factorQR(V)

В точности с плавающей точкой, продукте Q и R дает оригиналу 3×3 матричный V Вандермонда:

float(V) = Q*R

Сингулярное разложение

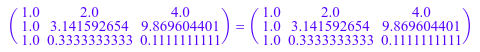
Сингулярное разложение выражает m ×n матричный A можно следующим образом: A = U  S V^H. Здесь S является m ×n диагональная матрица с сингулярными значениями A на его диагонали. Столбцы m ×m матричный U являются оставленными сингулярными векторами для соответствующих сингулярных значений. Столбцы n ×n матричный V являются правильными сингулярными векторами для соответствующих сингулярных значений. V ^H является Эрмитовым, транспонируют (сопряженное комплексное число транспонирования) V.

Чтобы вычислить сингулярное разложение матрицы, используйте numeric::svd или numeric::singularvectors функция. Эти две функции эквивалентны. Например, вычислите сингулярное разложение следующей матрицы:

A := matrix([[9, 4], [6, 8], [2, 7]]):
svd := numeric::svd(A)

Вместо того, чтобы возвратить диагональный матричный S, MuPAD возвращает список d из диагональных элементов той матрицы:

d := svd[2]

Можно восстановить матричный S из того списка:

S := matrix(3, 2, d, Diagonal)

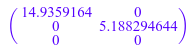
numeric::svd функция также вычисляет остатки res _U и res _V для числовых сингулярных векторов. Остатки являются предполагаемыми ошибками для числовых матриц U и V:

res_U = svd[4];
res_V = svd[5]

Маленькие значения остатка указывают, что ошибки округления не значительно влияют на результаты. Чтобы подавить расчет остатков, используйте NoResidues опция:

svd := numeric::svd(A, NoResidues)

В точности с плавающей точкой продукт U, S и Эрмитового транспонирует V, возвращает исходный матричный A:

[U, d, V, res_U, res_V] := svd:
A = U*S*conjugate(transpose(V))