numeric::singularvectorsЧисловое сингулярное разложение матрицы
Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
numeric::singularvectors(A, options)
numeric::singularvectors(A) и эквивалентный вызов numeric::svd(A) возвратите числовые сингулярные значения и сингулярные векторы матричного A.
Все записи A должно быть числовым. Числовые выражения такой как
и т.д. приняты и преобразованы в плавания. Нечисловые символьные записи приводят к ошибке.
Cat::Matrix объекты, т.е. матрицы A из матричной области, такой как Dom::Matrix(…) или Dom::SquareMatrix(…) внутренне преобразованы в массивы по выражениям через expr(A).
Список [U, d, V, resU, resV] возвращенный numeric::singularvectors соответствует сингулярным данным m ×n матричный A, аналогичный описанному ниже.
Позвольте V, H обозначает, что Эрмитовы транспонируют матричного V, т.е. сопряженного комплексного числа транспонирования. Сингулярное разложение m ×n матричный A является факторизацией A = U D VH. D является m ×n “диагональная” матрица с действительными неотрицательными записями D ii = d i, i = 1, …, p где p = min (m, n):
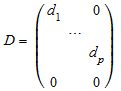
или
,
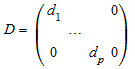соответственно. Список d = [d 1, …, d p] возвращенный numeric::singularvectors “сингулярные значения” A. Они сортируются по numeric::sort, т.е. d 1 ≥ … ≥ d p ≥ 0.0.
U является унитарный m ×m матрица. Его i-th столбец является собственным вектором A AH, сопоставленный с собственным значением d i 2 (d i = 0 для i> p). Это “левые сингулярные векторы” A. Они возвращены numeric::singularvectors как матрица чисел с плавающей запятой.
V является унитарный n ×n матрица. Его i-th столбец является собственным вектором A H A сопоставленный с собственным значением d i 2 (d i = 0 для i> p). Это “правильные сингулярные векторы” A. Они возвращены numeric::singularvectors как массив чисел с плавающей запятой. Матричный V нормирован таким образом, что в каждом столбце первая запись абсолютного размера, больше, чем
, действительна и положительна.
Если никакие не возвращаются, тип задан с помощью опции ReturnType = t, доменный тип сингулярных векторов U и V зависит от типа входной матрицы A:
Сингулярные векторы плотной матрицы типа Dom::DenseMatrix() возвращены как плотные матрицы типа Dom::DenseMatrix() по звонку выражений MuPAD®.
Для всех других матриц категории Cat::Matrix, сингулярные векторы возвращены как матрицы типа Dom::Matrix() по звонку выражений MuPAD. Это включает входные матрицы A из типа Dom::Matrix(…), Dom::SquareMatrix(…), Dom::MatrixGroup(…) и т.д.
res U = [resU 1, …, resU m] является списком остатков плавающих, сопоставленных с левыми сингулярными векторами:
.
Здесь, u i является (нормированный) i-th столбец U,
обычное комплексное Евклидово скалярное произведение и d i = 0 для p <i ≤ m.
res V = [resV 1, …, resV n] является списком остатков плавающих, сопоставленных с правильными сингулярными векторами:
.
Здесь, v i является (нормированный) i-th столбец V, d i = 0 для p <i ≤ n.
Остатки res U, res V исчезает для точных сингулярных данных U, d, V. Их размеры указывают на качество числовых данных U, d, V.
Сингулярные значения аппроксимированы абсолютной точностью
, где r является самым большим сингулярным значением A. Следовательно, большие сингулярные значения должны быть вычислены правильно к DIGITS десятичные разряды. Числовые приближения маленьких сингулярных значений менее точны.
Сингулярные данные могут также быть вычислены через [d2, U, resU] := numeric::eigenvectors(A*A^H) или [d2, V, resV] := numeric::eigenvectors(A^H*A), соответственно. Список d2 связан с сингулярными значениями
.
Использование numeric::singularvectors избегает затрат на умножение матриц. Далее, стандартная программа собственного вектора требует о вдвое больше DIGITS вычислить данные, сопоставленные с маленькими сингулярными значениями с той же точностью как numeric::singularvectors. Также обратите внимание что нормализация U и V может отличаться.
Функция чувствительна к переменной окружения DIGITS, который определяет числовую рабочую точность.
Числовые выражения преобразованы в плавания:
DIGITS := 5: A := array(1..3, 1..2, [[1, PI], [2, 3], [3, exp(sqrt(2))]]): [U, d, V, resU, resV] := numeric::singularvectors(A):
Сингулярные данные:
U, d, V
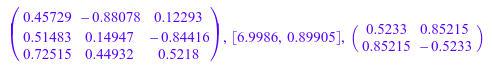
Маленькие остатки указывают, что эти результаты сильно не затронуты округлением:
resU, resV
delete DIGITS, A, U, d, V, resU, resV:
Мы демонстрируем, как восстановить матрицу из ее сингулярных данных. С заданным ReturnType, сингулярные векторы возвращены как матрицы типа Dom::Matrix() и может быть обработан с перегруженной арифметикой:
DIGITS := 3:
A := array(1..2, 1..3, [[1.0, I, PI], [2, 3, I]]):
[U, d, V, resU, resV] := numeric::singularvectors(A, NoResidues,
ReturnType = Dom::Matrix())
“Диагональная” матрица создается из сингулярных значений:
d := matrix(2, 3, d, Diagonal)
Мы используем методы conjugate и transpose из матричной области, чтобы вычислить Эрмитово транспонируют V и восстановите A. Числовое округление устраняется через numeric::complexRound:
VH := V::dom::conjugate(V::dom::transpose(V)): map(U*d*VH, numeric::complexRound)
delete DIGITS, A, U, d, V, resU, resV, VH:
Мы демонстрируем использование аппаратных плаваний. Следующий матричный A является вырожденным: это имеет ранг 1. Для двойного собственного значения 0 из матричного A H A, различные основные векторы соответствующего eigenspace возвращены с HardwareFloats и SoftwareFloats, соответственно:
A := array(1..2, 1..3, [[1, 2, 3], [30, 60, 90]]):
[U1, d1, V1, resU1, resV1] :=
numeric::singularvectors(A, HardwareFloats):
[U2, d2, V2, resU2, resV2] :=
numeric::singularvectors(A, SoftwareFloats):
V1, V2
delete A, U1, d1, V1, resU1, resV1, U2, d2, V2, resU2, resV2:
|
Числовая матрица доменный тип |
|
С С По сравнению с Если никакой Если результат не может быть вычислен с аппаратными плаваниями, арифметику программного обеспечения ядром MuPAD пробуют. Если текущее значение Может быть несколько причин аппаратной арифметики, чтобы перестать работать:
Если никакой Если Обратите внимание на то, что Запаздывающие цифры в результатах с плавающей точкой вычисляются с ПримечаниеДля плохо обусловленных матриц результат подвергается ошибкам округления. Результаты возвращены с |
|
Подавляет расчет левых сингулярных векторов Если только правильные сингулярные векторы требуются, эта опция может использоваться, чтобы подавить расчет В зависимости от размера |
|
Подавляет расчет правильных сингулярных векторов Если только левые сингулярные векторы требуются, эта опция может использоваться, чтобы подавить расчет В зависимости от размера |
|
Подавляет расчет ошибочных оценок Если никакие ошибочные оценки не требуются, эта опция может использоваться, чтобы подавить расчет остатков Альтернативная опция называет |
|
Опция, заданная как Возвратите левые и правые сингулярные векторы как матрицы доменного типа Эта опция определяет доменный тип матриц, содержащих сингулярные векторы. |
|
Отключает предупреждения |
Перечислите [U, d, V, resU, resV]U унитарная квадратная матрица плавающая, столбцам которой оставляют сингулярные векторы. Список d содержит сингулярные значения. V унитарная квадратная матрица плавающая, столбцы которой являются правильными сингулярными векторами. Списки остатков плавающих resU и resV обеспечьте ошибочные оценки для числовых данных.