Блокноты MuPAD® будут демонтированы в будущем релизе. Используйте live скрипты MATLAB® вместо этого.
Live скрипты MATLAB поддерживают большую часть функциональности MuPAD, хотя существуют некоторые различия. Для получения дополнительной информации смотрите, Преобразуют Notebook MuPAD в Live скрипты MATLAB.
Если int команда не может вычислить закрытую форму интеграла, MuPAD® возвращает неразрешенный интеграл:
int(sin(sinh(x)), x)
![]()
Если MuPAD не может вычислить интеграл выражения, одна из следующих причин может применяться:
Антипроизводная не существует в закрытой форме.
Антипроизводная существует, но MuPAD не может найти его.
Попытайтесь аппроксимировать эти интегралы при помощи одного из следующих методов:
Для неопределенных интегралов используйте последовательные расширения. Используйте этот метод, чтобы аппроксимировать интеграл вокруг особого значения переменной.
Для определенных интегралов используйте числовые приближения.
Если int не может вычислить неопределенный интеграл в закрытой форме, это возвращает неразрешенный интеграл:
F := int(cos(x)/sqrt(1 + x^2), x)
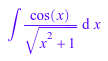
Чтобы аппроксимировать результат вокруг некоторой точки, используйте series функция. Например, аппроксимируйте интеграл вокруг x = 0:
series(F, x = 0)
![]()
Если вы знаете заранее, что интеграл не может быть найден в закрытой форме, пропуск, вычисляющий символьную форму интеграла. Чтобы использовать систему более эффективно, вызовите series команда, чтобы расширить подынтегральное выражение, и затем интегрировать результат:
int(series(cos(x)/sqrt(1 + x^2), x = 0), x)
![]()
Если int не может вычислить определенный интеграл в закрытой форме, это возвращает неразрешенный интеграл:
F := int(cos(x)/sqrt(1 + x^2), x = 0..10)
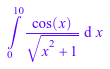
Чтобы аппроксимировать результат численно, используйте float функция:
float(F)
![]()
Если вы знаете заранее, что интеграл не может быть найден в закрытой форме, пропуск, вычисляющий символьную форму интеграла. Используйте систему более эффективно путем вызова numeric::int функция. Эта команда применяет числовые методы интегрирования с начала:
numeric::int(cos(x)/sqrt(1 + x^2), x = 0..10)
![]()