Документация

Используйте опции для узких результатов

По умолчанию решатели MuPAD^® возвращают все возможные решения независимо от своей длины. Кроме того, по умолчанию решатели принимают, что решения являются комплексными числами. Чтобы ограничить количество решений некоторых определенных единиц, решатели предоставляют много возможностей. Для получения информации об опциях, принятых конкретным решателем, смотрите страницу для того решателя. Например, для списка возможностей, предоставленных общим решателем, смотрите solve страница справки.

Следующее уравнение имеет пять решений:

solve(x^5 - 1, x)

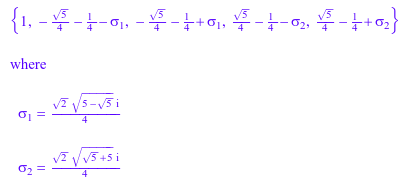
Если вам нужно решение в вещественных числах, используйте Real опция. Единственное действительное решение этого уравнения равняется 1:

solve(x^5 - 1, x, Real)

Для следующего стандартного квадратного уравнения решатель возвращает решения для всех возможных значений символьных параметров aB, и c:

solve(a*x^2 + b*x + c, x)

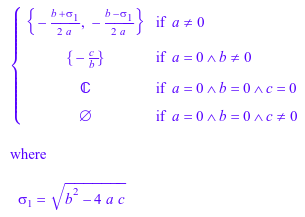
Чтобы игнорировать особые случаи, используйте IgnoreSpecialCases опция:

solve(a*x^2 + b*x + c, x, IgnoreSpecialCases)

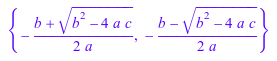
Для следующего уравнения решатель возвращает полное, а скорее долго и сложное решение:

solve(x^(5/2) + 1/x^(5/2) = 1, x)

Если вы хотите более простое и более практическое решение, попробуйте IgnoreAnalyticConstraints опция. При использовании этой опции решатель использует набор упрощенных математических правил, которые не обычно правильны. Возвращенные решения имеют тенденцию быть самыми полезными для многих проблем в разработке и физике. Обратите внимание на то, что с этой опцией решатель не гарантирует правильности и полноты результата:

solve(x^(5/2) + 1/x^(5/2) = 1, x, IgnoreAnalyticConstraints)

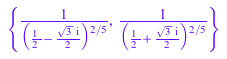
См. список опций, принятых общим решателем solve.

Используйте предположения узким результатам

Если вы хотите ограничить количество решений, но список опций, доступных для solve не имеет подходящего варианта, пытаются использовать предположения. Предположим для следующего многочленного выражения, вам нужны только положительные решения. Используйте assuming команда, чтобы временно принять тот x положительное число. Под этим предположением решатель возвращает четыре положительных решения:

solve(x^7 + 2*x^6 - 59*x^5 - 106*x^4 + 478*x^3 + 284*x^2
      - 1400*x + 800, x) assuming x > 0

Без предположения решатель возвращает все семь решений:

solve(x^7 + 2*x^6 - 59*x^5 - 106*x^4 + 478*x^3 + 284*x^2
      - 1400*x + 800, x)

Чтобы сделать несколько предположений, объедините их с and:

solve([a*x + b*y = c, h*x - g*y = f], [x, y])
      assuming f = c and a = h and a <> 0

{ { --     f + g z        -- }
{ { |  x = -------, y = z  | }  if  b + g = 0
{ { --        h           -- }
{
{    { --     f        -- }
{    { |  x = -, y = 0  | }     if  b + g <> 0
{    { --     h        -- }

Для получения дополнительной информации смотрите Свойства и Предположения.

Упростите решения

При решении уравнений MuPAD автоматически упрощает много объектов, таких как некоторые вызовы функции и арифметические выражения с числами. Автоматические упрощения уменьшают сложность выражений, используемых на промежуточных шагах, который улучшает производительность решателей.

Решатели MuPAD не вызывают функции упрощения для конечных результатов. Когда вы вызываете solve команда, можно получить долгое и сложное решение:

S := solve((sin(x/2) - cos(x/2))/(sin(x/2) + cos(x/2)) = I/2, x)

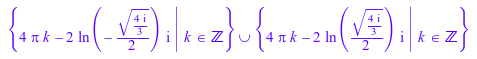
Чтобы упростить такие результаты, используйте simplify или Simplify. simplify функция быстрее:

simplify(S)

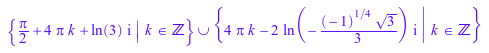
Simplify медленнее, но более мощен:

Simplify(S)

Для получения дополнительной информации смотрите Упрощение.