Документация

Увеличьте число шагов упрощения

При упрощении сложного выражения MuPAD^® может возвратить результаты, которые извлекли бы выгоду из дальнейших упрощений. Предположим, что вы хотите упростить следующее выражение:

f := (-(4*PI*3^(1/2))/3 + PI*(-1)^(3/4)*2^(1/2)*3^(1/2)
      *(- (2*I)/3 - 2/3))*(cos(3*arccos(x)))

Во-первых, попытайтесь вызвать общий simplifier simplify:

simplify(f)

Возвращенное выражение имеет еще более короткое представление. Чтобы упростить этот результат далее, вызовите Simplify команда:

Simplify(f)

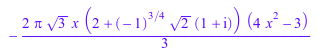
Можно упростить результат еще больше путем увеличения числа шагов:

Simplify(f, Steps = 150)

Примените несколько функций упрощения

Чтобы преобразовать очень сложное выражение или выражение, которое должно появиться в конкретной форме, вы можете должны быть применить несколько функций упрощения. То, когда вы преобразовываете выражение к конкретной форме при помощи специальной функции преобразования, функция может возвратиться, может возвратить результаты, которые не полностью упрощены. Предположим, что вы хотите переписать тригонометрическое выражение в терминах показательных функций. rewrite команда заменяет sin и cos функции показательными функциями, но не упрощает результат:

f := rewrite(sin(x)/cos(x), exp)

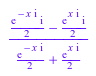
Чтобы упростить получившееся выражение, вызовите simplify команда:

simplify(f)

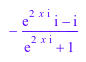
Более мощный Simplify функция преобразует это выражение назад в его тригонометрическую форму:

Simplify(f)

Используйте опции

При преобразовании выражений MuPAD simplifiers применяет правила, допустимые для целой комплексной плоскости. Например, попытайтесь упростить это выражение, содержащее логарифмы:

h := ln(x + 1)/2 - ln(1 - 1/x)/2 - ln(1 - x)/2 + ln(1/x + 1)/2

По умолчанию simplifier не комбинирует логарифмы, потому что эта операция только допустима для конкретных вещественных чисел. Для комплексных чисел объединение логарифмов не обычно допустимо:

Simplify(h)

Если вы решаете задачу, которая не требует приложения строгих математических правил, пытается использовать IgnoreAnalyticConstraints опция. При использовании этой опции simplifier использует набор математических правил, которые не обычно правильны. Например, если вы используете IgnoreAnalyticConstraints опция, simplifier возвращается:

Simplify(h, IgnoreAnalyticConstraints)

Результаты получили с опцией IgnoreAnalyticConstraints являются самыми полезными для многих в проблемах разработки и физики. Обратите внимание на то, что, когда вы используете эту опцию, simplifiers не гарантируют эквивалентности исходных и упрощенных выражений для целой комплексной плоскости.

Используйте предположения

При преобразовании выражения функции упрощения применяют правила, допустимые для целой плоскости комплексных чисел. По умолчанию MuPAD не принимает дополнительных математических свойств на идентификаторах. Например, идентичность не обычно допустима для всех комплексных чисел:

simplify(ln(exp(x)))

Когда вы работаете с вещественными числами, функции упрощения могут также использовать правила, допустимые для вещественных чисел. Используйте assume или assuming команда, чтобы указать, что переменная x представляет вещественное число. assume команда создает постоянное предположение. assuming команда создает временное предположение, которое допустимо во время одной команды. simplifier применяет соответствующее правило и возвращает ожидаемый результат:

simplify(ln(exp(x))) assuming x in R_

Когда вы упрощаете следующее выражение, возвращенное выражение короче, чем исходное. Однако можно далее упростить возвращенное выражение:

f := ln(- 2*sin(-(sin(x)*I)/2)^2 + sin(-sin(x)*I)*I + 1);
Simplify(f)

Увеличение числа шагов упрощает выражение далее:

Simplify(f, Steps = 300)

Если вы хотите получить упрощенный результат для действительного x, примите тот x isreal:

assume(x, Type::Real);
Simplify(f, Steps = 300)

Чтобы удалить предположение, используйте unassume команда:

unassume(x);
is(x, Type::Real)

При принятии любого дополнительного математического свойства для переменной (такой как принятие, что x действительно), убедитесь, что ваша проблема не требует решений быть допустимой для всех комплексных чисел. Будьте особенно осторожны, если ваше начальное выражение содержит комплексные числа.

Для получения дополнительной информации о предположениях, смотрите Свойства и Предположения.