Документация

Задайте правую сторону уравнения

Решатель принимает и уравнения и выражения. Если вы вызываете solve для выражения команда принимает правую сторону, чтобы быть 0:

S1 := solve(x^3 - 1, x);
S2 := solve(x^3 = 8, x);
S3 := solve(x^3 - 3*x^2 = 1 - 3*x, x)

Присвойте отдельные решения переменных путем индексации в результат:

sol := S1[3]

Задайте переменные уравнения

Определение переменной, для которой вы хотите решить уравнение, является дополнительным. Если вы задаете переменную, solve команда возвращает решения как набор чисел. В противном случае команда возвращает набор списков как решение:

solve(x^2 - 3*x + 2 = 0, x);
solve(x^2 - 3*x + 2 = 0)

Если ваше уравнение содержит символьные параметры, задайте переменную, для которой вы хотите решить уравнение:

solve(a*x^2 + b*x + c, x)

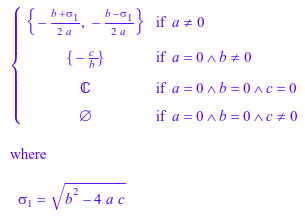
Если вы решаете уравнение символьными параметрами и не задаете переменную, solve использование все параметры как переменные и возвращает набор всех возможных решений. Например, решая следующее уравнение решатель принимает это оба x и y свободные переменные. при возврате всех возможных решений для этого уравнения решатель использует произвольный параметр z:

solve(x^3 + y^3)

Чтобы задать больше чем одну переменную, предоставьте список переменных в качестве второго аргумента:

solve(a*x^2 + b*x + c, [a, b, c])

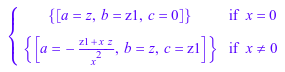
solve также может возвратить выражение как x in S, где x список переменных, для которых вы решаете уравнение и S набор векторов решения:

solve(a*x + 1/x)

Решите полиномиальные уравнения высшего порядка

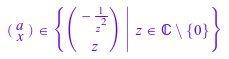
Когда вы решаете полиномиальное уравнение высшего порядка, решатель иногда использует RootOf возвратить результаты:

solve(x^3 + 2*x + 1 = 0, x)

Чтобы получить явное решение для таких уравнений, попытайтесь вызвать решатель с опцией MaxDegree. Опция задает максимальную степень полиномов, для которых решатель пытается возвратить явные решения. По умолчанию, MaxDegree=2. Увеличивая это значение, можно получить явные решения для полиномов высшего порядка. Например, задайте MaxDegree=3 и получите явные решения вместо RootOf для полинома третьего порядка:

solve(x^3 + 2*x + 1 = 0, x, MaxDegree = 3)

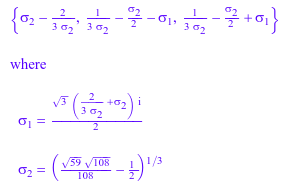
Когда вы решаете пятую часть - или полиномиальное уравнение высшего порядка, решатель может не мочь возвратить решение явным образом, даже с опцией MaxDegree:

solve(x^5 + 2*x + 1 = 0, x);
solve(x^5 + 2*x + 1 = 0, x, MaxDegree = 5)

В общем случае нет никаких явных выражений для корней полиномов степеней выше, чем 4. Установка опции MaxDegree к 4 или более высокое значение не имеет никакого значения.

RootOf символически представляет набор корней полинома. Можно использовать выражения, содержащие RootOf в ваших дальнейших расчетах. Например, найдите сумму по всем корням полинома:

sum(S^2 + S + 2, S in RootOf(X^5 + 2*X + 1, X));

Чтобы получить числовое приближение корней, используйте float команда:

float(RootOf(X^4 + X + 1, X))

Для получения дополнительной информации о числовых приближениях смотрите уравнения Решения Численно.

Для одномерных полиномиальных уравнений MuPAD^® также может вычислить интервалы, содержащие действительные корни. Смотрите Изолирующие Действительные Корни Полиномиальных уравнений.

Найдите несколько корней

По умолчанию, solve команда не возвращает кратность корней. Когда решение уравнения содержит несколько корней, MuPAD удаляет копии:

solve(x^2 - 6*x + 9 = 0, x)

Решатель не отображает несколько корней, потому что он возвращает результаты как набор. Набор в MuPAD не может содержать дублирующиеся элементы. Чтобы получить полиномиальные корни с их кратностью, используйте опцию Multiple:

solve(x^2 - 6*x + 9 = 0, x, Multiple);
solve((x - 1)^3*(x - 2)^7, x, Multiple)

Изолируйте действительные корни полиномиальных уравнений

Для некоторых полиномиальных уравнений решатель не может возвратить явные символьные решения.

p:= x^5 - 31*x^4/32 + 32*x^3/33 - 33*x^2/34 - 34*x/35 + 35/36:
solve(p, x)

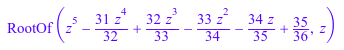
Если вы предпочитаете решение в форме кроме RootOf и хочу избежать числовых методов, использовать polylib::realroots найти все интервалы, содержащие действительные решения:

p:= x^5 - 31*x^4/32 + 32*x^3/33 - 33*x^2/34 - 34*x/35 + 35/36:
polylib::realroots(p)

Решите неравенства

solve может решить неравенства. Как правило, набором решения неравенства является interval или объединение интервалов:

solve(x^2 > 5, x)

Используйте solve решить следующее неравенство. Решение включает набор всех комплексных чисел, исключая и:

solve(x^2 <> 7, x)