Шумоподавление мультисигнала 1-D с помощью вейвлетов
[XD,DECDEN,THRESH] = mswden('den',...)
[XD,THRESH] = mswden('densig',...)
[DECDEN,THRESH]
= mswden('dendec',...)
THRESH = mswden('thr',...)
[...] = mswden(OPTION,DIRDEC,X,WNAME,LEV,METH,PARAM)
[...] = mswden(...,S_OR_H)
[...]
= mswden(...,S_OR_H,KEEPAPP)
[...]
= mswden(...,S_OR_H,KEEPAPP,IDXSIG)
mswden вычисляет пороги и, в зависимости от выбранной опции, выполняет шумоподавление 1D сигналов с помощью вейвлетов.
[XD,DECDEN,THRESH] = mswden('den',...) возвращает denoised версию XD из исходного матричного X мультисигнала, чьей структурой разложения вейвлета является DEC. Выход XD получен пороговой обработкой коэффициенты вейвлета, DECDEN разложение вейвлета, сопоставленное к XD (см. mdwtdec), и THRESH матрица пороговых значений. Вход METH имя метода шумоподавления и PARAM связанный параметр, при необходимости.
Допустимые методы шумоподавления METH и сопоставленные параметры PARAM :
'rigrsure' | Принцип несмещенного риска глиняной кружки |
'heursure' | Эвристический вариант права преимущественной покупки |
'sqtwolog' | Универсальный порог |
'minimaxi' | Минимаксная пороговая обработка (см. |
Для этих методов PARAM задает мультипликативное пороговое перемасштабирование:
'one' | Никакое перемасштабирование |
'sln' | Перемасштабирование использования одной оценки шума уровня на основе первых коэффициентов уровня |
'mln' | Перемасштабирование использования зависимой оценки уровня шума уровня |
'penal' | Уголовный |
'penalhi' | Уголовный высокий, |
'penalme' | Уголовный носитель, |
'penallo' | Уголовный низкий, |
PARAM параметр разреженности, и это должно быть таково что: 1 ≤ PARAM≤ 10 . Для penal метод, никакое управление не сделано.
'man_thr' | Ручной метод |
PARAM NbSIG- NbLEV матрица или NbSIG- (NbLEV+1) матрицируйте таким образом что:
PARAM(i,j) порог для коэффициентов детали уровня j для сигнала ith (1 ≤ j ≤ NbLEV).
PARAM(i,NbLEV+1) порог для коэффициентов приближения для iсигнал th (если KEEPAPP 0).
где NbSIG количество сигналов и NbLEV количество уровней разложения.
Вместо 'den' вход OPTION, можно использовать 'densig', 'dendec' или 'thr' OPTION выбрать выходные аргументы:
[XD,THRESH] = mswden('densig',...) или [DECDEN,THRESH]
= mswden('dendec',...)
THRESH = mswden('thr',...) возвращает вычисленные пороги, но шумоподавление не выполняется.
Входной параметр структуры разложения DEC может быть заменен четырьмя аргументами: DIRDECX, WNAME и LEV.
[...] = mswden(OPTION,DIRDEC,X,WNAME,LEV,METH,PARAM) прежде, чем выполнить шумоподавление или вычислить пороги, матричный X мультисигнала анализируется на уровне LEV использование вейвлета WNAME, в направлении DIRDEC.
Можно использовать еще три дополнительных входных параметров:
[...] = mswden(...,S_OR_H) или
[...]
= mswden(...,S_OR_H,KEEPAPP) или
[...]
= mswden(...,S_OR_H,KEEPAPP,IDXSIG)
S_OR_H ('s' or 'h') обозначает мягкую или трудную пороговую обработку (см. mswthresh для получения дополнительной информации).
KEEPAPP (true or false) указывает, сохранить ли коэффициенты приближения (true) или не (false).
IDXSIG вектор, который содержит индексы начальных сигналов или 'all'.
Значениями по умолчанию является, соответственно, 'h'ложь и 'all'.
% Load original 1D-multisignal.
load thinker
% Perform a decomposition at level 2 using the wavelet db2.
dec = mdwtdec('r',X,2,'db2');
% Denoise signals using the universal method
% of thresholding (sqtwolog) and the 'sln'
% threshold rescaling (with a single estimation
% of level noise, based on first level coefficients).
[XD,decDEN,THRESH] = mswden('den',dec,'sqtwolog','sln');
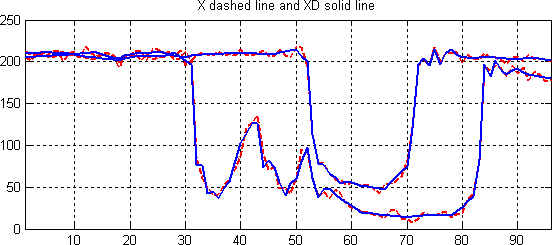
% Plot the original signals 1 and 31, and the
% corresponding denoised signals.
figure;
plot(X([1 31],:)','r--','linewidth',2); hold on
plot(XD([1 31],:)','b','linewidth',2);
grid; set(gca,'Xlim',[1,96])
title('X dashed line and XD solid line')
Birgé, Л.; П. Мэссарт (1997), “От выбора модели до адаптивной оценки”, в Д. Полларде (редактор), Festchrift для Ль. Ле Кама, Спрингера, стр 55–88.
DeVore, Р.А.; Б. Джейрт, Б.Дж. Лукир (1992), “Сжатие изображения через вейвлет преобразовывает кодирование”, Сделка IEEE на Inf. Теория, издание 38, № 2, стр 719–746.
Donoho, D.L. (1993), “Прогресс анализа вейвлета и WVD: десятиминутный тур”, происходящий в анализе вейвлета и приложениях, И. Мейере. Роке, стр 109–128. Фронтиерес Эд.
Donoho, Д.Л.; И.М. Джонстон (1994), “Идеальная пространственная адаптация уменьшением вейвлета”, Biometrika, издание 81, стр 425–455.
Donoho, Д.Л.; И.М. Джонстон, Г. Керкьячариэн, Д. Пикар (1995), “Уменьшение вейвлета: asymptopia”, Подмастерье. Рой. Закон Soc.,series B, издание 57 № 2, стр 301–369.
Donoho, Д.Л.; И.М. Джонстон, “Идеальное шумоподавление в ортонормированном базисе, выбранном из библиотеки основ”, C.R.A.S. Париж, t. 319, Сер. Я, стр 1317–1322.
Donoho, D.L. (1995), “Шумоподавление мягкой пороговой обработкой”, Сделка IEEE на Inf. Теория, 41, 3, стр 613–627.