2D разложение вейвлета
Для изображений алгоритм, похожий на одномерный случай, возможен для двумерных вейвлетов и масштабирующихся функций, полученных из одномерных векторов продуктом тензора. Этот вид двумерного DWT приводит к разложению коэффициентов приближения на уровне j в четырех компонентах: приближение на уровне j +1 и детали в трех ориентациях (горизонталь, вертикальная, и диагональная).
График описывает основной шаг разложения для изображений:

где
![]() — Столбцы Downsample: сохраните ровные индексированные столбцы.
— Столбцы Downsample: сохраните ровные индексированные столбцы.
![]() — Строки Downsample: сохраните даже индексированные строки.
— Строки Downsample: сохраните даже индексированные строки.
![]() — Примените операцию свертки с фильтром к X строки записи.
— Примените операцию свертки с фильтром к X строки записи.
![]() — Примените операцию свертки с фильтром к X строки записи.
— Примените операцию свертки с фильтром к X строки записи.
и
Инициализация: cA 0 = s.
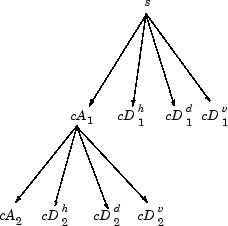
Так, для J = 2, двумерное дерево вейвлета имеет форму
[1] Daubechies, я. Десять лекций по вейвлетам, CBMS-NSF региональный ряд конференции в прикладной математике. Филадельфия, PA: SIAM Эд, 1992.
[2] Mallat, S. G. “Теория для Разложения Сигнала Мультиразрешения: Представление Вейвлета”, Транзакции IEEE согласно Анализу Шаблона и Искусственному интеллекту. Издание 11, Выпуск 7, июль 1989, стр 674–693.
[3] Мейер, Y. Вейвлеты и операторы. Переведенный Д. Х. Сэлинджером. Кембридж, Великобритания: Издательство Кембриджского университета, 1995.