Exponenta Banner

dwt2

Одноуровневый дискретный 2D вейвлет преобразовывает

свернуть все на странице

Синтаксис

[cA,cH,cV,cD] = dwt2(X,wname)
[cA,cH,cV,cD] = dwt2(X,LoD,HiD)
[cA,cH,cV,cD] = dwt2(___,'mode',extmode)

Описание

dwt2 вычисляет одноуровневое 2D разложение вейвлета. Сравните dwt2 с wavedec2 который может быть более полезен для вашего приложения. Разложение сделано относительно любого конкретный вейвлет (см. wfilters для получения дополнительной информации) или конкретные фильтры разложения вейвлета.

пример

[cA,cH,cV,cD] = dwt2(X,wname) вычисляет одноуровневый 2D дискретный вейвлет преобразовывает (DWT) входных данных X использование wname вейвлет. dwt2 возвращает содействующую матрицу приближения cA и подробно изложите содействующие матрицы cH, cV, и cD (горизонталь, вертикальная, и диагональная, соответственно).

пример

[cA,cH,cV,cD] = dwt2(X,LoD,HiD) вычисляет одноуровневый 2D DWT использование разложения вейвлета фильтр lowpass LoD и highpass фильтруют HiD. Фильтры разложения должны иметь ту же длину.

[cA,cH,cV,cD] = dwt2(___,'mode',extmode) вычисляет одноуровневый 2D DWT с дополнительным режимом extmode. Включайте этот аргумент после всех других аргументов.

Примеры

свернуть все

Скрипт Open Live Script

Загрузите и отобразите изображение.

load woman
imagesc(X)
colormap(map)

Получите одноуровневое 2D дискретное преобразование вейвлета изображения с помощью порядка 4 symlet и периодического расширения.

[cA,cH,cV,cD] = dwt2(X,'sym4','mode','per');

Отобразите вертикальные коэффициенты детали и коэффициенты приближения.

imagesc(cV)
title('Vertical Detail Coefficients')

imagesc(cA)
title('Approximation Coefficients')

Скрипт Open Live Script

Загрузите и отобразите изображение.

load sculpture
imagesc(X)
colormap gray

Сгенерируйте lowpass и highpass фильтры разложения для вейвлета Хаара.

[LoD,HiD] = wfilters('haar','d');

Используйте фильтры, чтобы выполнить одноуровневое 2D разложение вейвлета. Используйте полуточку симметричное расширение. Отобразите приближение и детализируйте коэффициенты.

[cA,cH,cV,cD] = dwt2(X,LoD,HiD,'mode','symh');
subplot(2,2,1)
imagesc(cA)
colormap gray
title('Approximation')
subplot(2,2,2)
imagesc(cH)
colormap gray
title('Horizontal')
subplot(2,2,3)
imagesc(cV)
colormap gray
title('Vertical')
subplot(2,2,4)
imagesc(cD)
colormap gray
title('Diagonal')

Входные параметры

свернуть все

Входные данные, заданные как m- n матрица, представляющая индексируемое изображение или m- n- 3 массива, представляющие изображение истинного цвета. Для получения дополнительной информации об изображениях истинного цвета смотрите RGB (Истинный цвет) Изображения (MATLAB).

Типы данных: double

Анализ вейвлета использовался для расчета 2D DWT, заданного как скаляр строки или вектор символов. Вейвлет анализа от одного из следующих семейств вейвлетов: Daubechies, Coiflets, Symlets, Fejér-Korovkin, Дискретный Мейер, Биоортогональный, и Противоположный Биоортогональный. Смотрите wfilters для вейвлетов, доступных в каждом семействе.

Разложение вейвлета фильтр lowpass, заданный как ровная длина вектор с действительным знаком. LoD должен иметь ту же длину как HiD.

Разложение вейвлета highpass фильтр, заданный как ровная длина вектор с действительным знаком. HiD должен иметь ту же длину как LoD.

Дополнительный режим, используемый при выполнении DWT, заданного как одно из следующего:

mode

Режим расширения DWT

'zpd'

Дополнение нулями

'sp0'

Сглаживайте расширение порядка 0

'spd' (or 'sp1')

Сглаживайте расширение порядка 1

'sym' или 'symh'

Симметричное расширение (половина точки): граничное значение симметричная репликация

'symw'

Симметричное расширение (самое главное): граничное значение симметричная репликация

'asym' или 'asymh'

Антисимметричное расширение (половина точки): граничное значение антисимметричная репликация

'asymw'

Антисимметричное расширение (самое главное): граничное значение антисимметричная репликация

'ppd'

Расширение Periodized (1)

'per'

Расширение Periodized (2)

Если длина сигнала нечетна, wextend добавляет направо дополнительную выборку, которая равна последнему значению и выполняет расширение с помощью 'ppd' режим. В противном случае, 'per' уменьшает до 'ppd'. Это правило также применяется к изображениям.

Глобальная переменная, управляемая dwtmode задает режим расширения по умолчанию.

Пример: [cA,cH,cV,cD] = dwt2(x,'db4','mode','symw');

Выходные аргументы

свернуть все

Коэффициенты приближения, возвращенные как массив, размер которого зависит от X. Позвольте sx = size(X) и lf = длина фильтров разложения.

  • Если дополнительный режим DWT установлен в periodization, то этот выход имеет размер ceil(sx/2).

  • Для других дополнительных режимов этот выход имеет размер floor((sx+lf-1)/2).

Типы данных: double

Горизонтальные коэффициенты детали, возвращенные как массив, размер которого зависит от X. Позвольте sx = size(X) и lf = длина фильтров разложения.

  • Если дополнительный режим DWT установлен в periodization, то этот выход имеет размер ceil(sx/2).

  • Для других дополнительных режимов этот выход имеет размер floor((sx+lf-1)/2).

Типы данных: double

Вертикальные коэффициенты детали, возвращенные как массив, размер которого зависит от X. Позвольте sx = size(X) и lf = длина фильтров разложения.

  • Если дополнительный режим DWT установлен в periodization, то этот выход имеет размер ceil(sx/2).

  • Для других дополнительных режимов этот выход имеет размер floor((sx+lf-1)/2).

Типы данных: double

Диагональные коэффициенты детали, возвращенные как массив, размер которого зависит от X. Позвольте sx = size(X) и lf = длина фильтров разложения.

  • Если дополнительный режим DWT установлен в periodization, то этот выход имеет размер ceil(sx/2).

  • Для других дополнительных режимов этот выход имеет размер floor((sx+lf-1)/2).

Типы данных: double

Алгоритмы

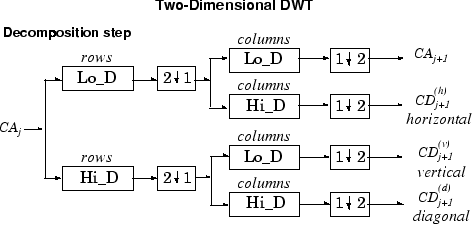
2D алгоритм разложения вейвлета для изображений похож на одномерный случай. Двумерный вейвлет и масштабирующиеся функции получены путем взятия продуктов тензора одномерного вейвлета и масштабирования функций. Этот вид двумерного DWT приводит к разложению коэффициентов приближения на уровне j в четырех компонентах: приближение на уровне j + 1, и детали в трех ориентациях (горизонталь, вертикальная, и диагональная). Следующий график описывает основные шаги разложения для изображений.

  • — Столбцы Downsample: сохраните ровные индексированные столбцы

  • — Строки Downsample: сохраните ровные индексируемые строки

  • — Примените операцию свертки с фильтром X строки записи

  • — Примените операцию свертки с фильтром X столбцы записи

Разложение инициализируется путем установки коэффициентов приближения, равных изображению s: CA0=s.

Примечание

Чтобы иметь дело с эффектами конца сигнала, введенными основанным на свертке алгоритмом, 1D и 2D DWT используют глобальную переменную, управляемую dwtmode. Эта переменная задает вид дополнительного используемого режима сигнала. Возможные варианты включают дополняющее нуль и симметричное расширение, которое является режимом по умолчанию.

Ссылки

[1] Daubechies, я. Десять лекций по вейвлетам, CBMS-NSF региональный ряд конференции в прикладной математике. Филадельфия, PA: SIAM Эд, 1992.

[2] Mallat, S. G. “Теория для Разложения Сигнала Мультиразрешения: Представление Вейвлета”, Транзакции IEEE согласно Анализу Шаблона и Искусственному интеллекту. Издание 11, Выпуск 7, июль 1989, стр 674–693.

[3] Мейер, Y. Вейвлеты и операторы. Переведенный Д. Х. Сэлинджером. Кембридж, Великобритания: Издательство Кембриджского университета, 1995.

Расширенные возможности

Генерация кода C/C++
Генерация кода C и C++ с помощью MATLAB® Coder™.

Смотрите также

| | | | | | |

Представлено до R2006a

Документация Wavelet Toolbox
Поддержка